方差为什是是除以(n-1)而不是除以n啊

Posted 2023-03-30

样本方差之所以要除以（n-1）是因为这样的方差估计量才是关于总体方差的无偏估计量。这个公式是通过修正下面的方差计算公式而来的：

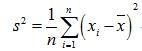
修正过程为：

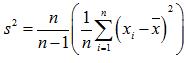
1、方差计算公式：  

2、 均值的均值、方差计算公式：

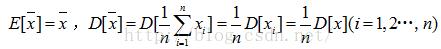
对于没有修正的方差计算公式我们有： 

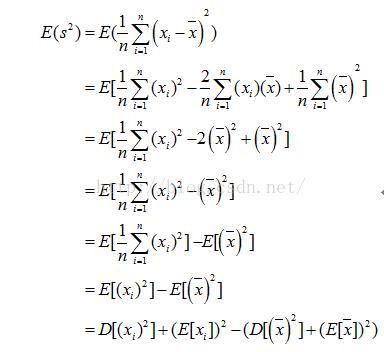
因为：

所以有：

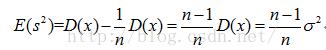
在这里如果想修正的方差公式，让修正后的方差公式求出的方差的期望为总体方差的话就需要在没有修正的方差公式前面加上来进行修正，即：

所以就会有这样的修正公式：

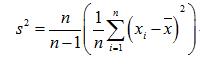
修正后的最终结果：

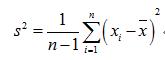
扩展资料：  

方差的性质

1、设C是常数，则D（C）=0

2、设X是随机变量，C是常数，则有

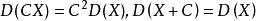
3、设 X 与 Y 是两个随机变量，则

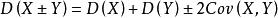
其中协方差

特别的，当X，Y是两个不相关的随机变量则

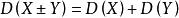
此性质可以推广到有限多个两两不相关的随机变量之和的情况。

4、D（X）=0的充分必要条件是X以概率1取常数E（X），即

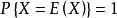
（当且仅当X取常数值E（X）时的概率为1时，D（X）=0。）

注：不能得出X恒等于常数，当x是连续的时候X可以在任意有限个点取不等于常数c的值。

5、D（aX+bY）=a2DX+b2DY+2abCov（X，Y）。

参考资料来源：百度百科-方差    

参考技术A

这是为了达到对总体方差的无偏估计。你可以计算下样本方差的期望值：

这样，当样本数量足够多时，样本方差就可以逼近总体方差（因为其期望是总体方差）。也就是说达到了总体方差的无偏估计。

【要分清样本方差和总体方差的区别】

本回答被提问者和网友采纳 参考技术B 这个是无偏估计，自由度减一 参考技术C 忘记了。。 参考技术D 好深奥啊，我去百度看看。。。。追问

这是概率论书上的定义

追答

找到了一些介绍。
方差的定义是除以n。
样本方差的定义是除以n-1。

为什么样本方差除以（n-1）而不是n ?

　　不记得第几次看见样本方差的公式，突然好奇为什么要除以（n-1）而不是n呢？看见一篇文章从定义上和无偏估计推导上讲的很清楚https://blog.csdn.net/fuming2021118535/article/details/51290320，书上看见从自由度上作的解释，在此记录一下。

　　自由度

　　自由度是统计学中一个经常见到的重要概念。指计算某一统计量时，取值不受限制的变量个数。

　　对于样本方差来说，自由度为n-1。S²的表达式中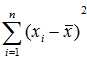为n个量的平方和，为何自由度只有n-1?因为x₁-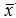, ... , x₂-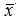这n个量并不能自由变化，而是受到一个约束，即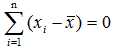，这使它的自由度少了一个，在样本方差S²的公式中分母上是n-1，就是因为当给定均值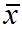时，x₁, x₂, ..., x_n这n个数据中，前n-1个数据都可以自由取值，而第n个数据受到全部数据的平均值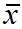的约束，不能自由取值。第n个数据可由公式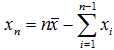求得，因此，S²的自由度是n-1。所以，所谓“自由度”就是指可以自由取值的数据的个数，或者指不受任何约束，可以自由变动的变量的个数。

　　还可以对自由度这个概念赋予另一种解释，即一共有n个数据，有n个自由度，用S²估计总体方差σ²，自由度本应为n，但总体均值μ也未知，用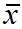去估计，用掉了一个自由度，故只剩n-1个自由度。

　　用矩阵秩的概念也可以解释自由度。自由度是对随机变量的二次型（可称为二次统计量）而言的，自由度就是二次型矩阵的秩。但用矩阵的秩来判断统计量的自由度比较困难，一般采用直观方法来做判断，即由线性代数知识可知，一个二次型的秩为它所含变量个数减去变量间独立线性约束条件的个数，从而便可得到统计量的自由度。关于样本方差S²的自由度，就是因为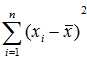含有n个变量，但n个变量有一个线性约束条件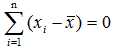，故S²的自由度为n-1。

　　回归分析中，回归方程的显著性检验用到残差平方和。确定残差平方和的自由度的一般方法是：观测值的个数n减去必须估计出的参数的个数就是自由度。例如p元线性回归方程的残差平方和的自由度就是n-p-1，因为回归方程中有p+1个待估参数。