虎书学习笔记3:图形学基础数学(正交基与坐标系二维梯度)
Posted Mario cai
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了虎书学习笔记3:图形学基础数学(正交基与坐标系二维梯度)相关的知识,希望对你有一定的参考价值。
关于图形学的基础数学知识
基础数学
标准正交基与坐标系(单位向量互相垂直构成坐标系)
任意两个二位向量,只要他们正交,长度为单位长度,就可构成一个标准正交基
三维中三个向量符合这个条件也构成标准正交基
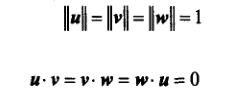
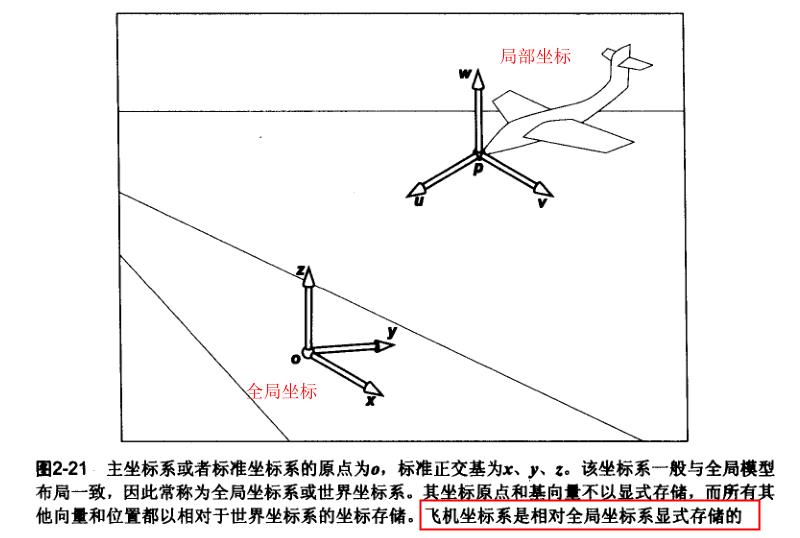
全局模型储存在的坐标系:全局坐标系
另外的原点p,标准正交基不同的坐标系,我们就要显示储存这些向量。这样的坐标系我们称为参考坐标系。
例如:飞机模拟器
我们有一个全局坐标系
我们也还需要一个位于飞机体的坐标:参考坐标系
参考坐标系能通过全局坐标系转换得来(转换矩阵)

单位向量建立正交基(建立局部坐标系用)
已知一个向量a,需要找出一个标准正交向量u,v,m,使得w的指向与a向量方向相同:
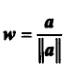
然后求u,v,需要找到与w不共线的向量t,只要t等于w再将最小的元素变成1: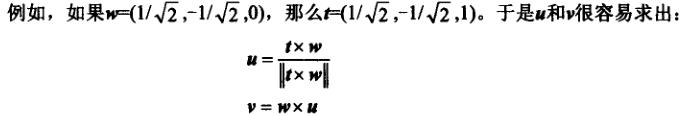
##二维隐式曲线(一种表示几何的函数)
一条曲线可以理解为一群点的集合,可以用隐式方程。方程如下:

这个方程可以理解为圆心为(xc,yc),半径为r的圆,函数值为0则点在圆上。
因为需要将点(x,y)代入才能看出,所以叫隐式方程。
函数f可以看成一个海平面,f等于0大于0小于0三个区域
可以通过代入点(x,y)判断是否在曲线上。
f=0是最基础的方式,然而f可以有不同的值。如图:
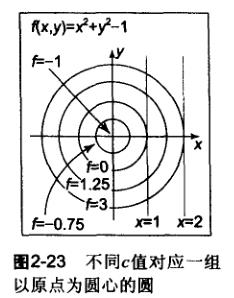
可以使用向量简化f(x,y),
可以看出以下性质:点c到点p的向量与自身点积结果为r的平方

简单的解释为:圆周上的点p,就是那些到圆心c的距离为r的点。
二维梯度(对应多种变化所以必须求偏导)
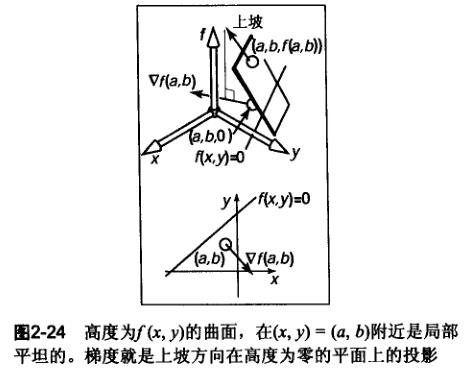
将函数f(x,y)看成高度为f(x,y)的高度图,梯度向量就是指向坡度最大的方向,梯度向量一般就用求偏导得出。
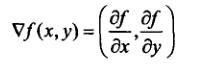
曲线法向量:如果f(x,y)=0,某点梯度向量与曲线在该点处的切向量正交。该梯度向量称为曲线的法向量。
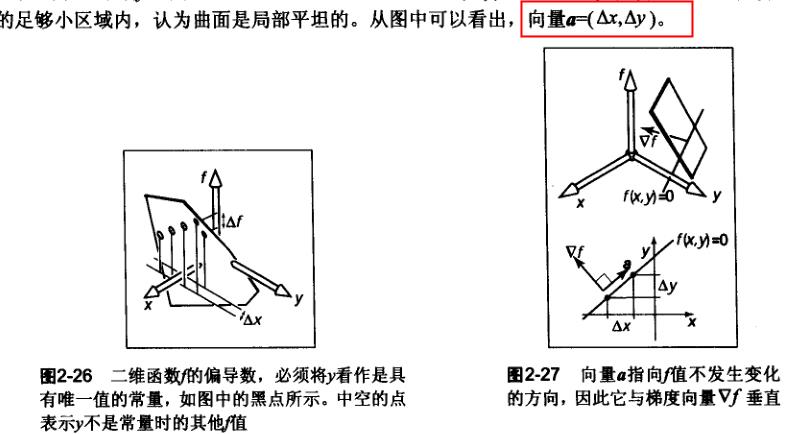
偏导数的几何意义,假设一维函数y,求偏导可拆分为:
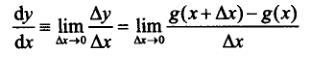
可视化一下:
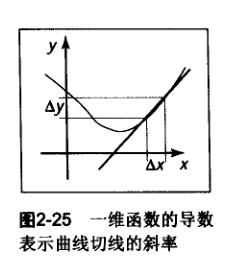
就是切线的斜率。
试着观看高度图情况下,偏导数和梯度的可视化。
例如:假设点(a,b)附近是一个平面。有明确的上坡和下坡,与上坡下坡方向垂直的方向就是该平面的水平方向。
该平面与平面f(x,y)=0的任意交线都将在这个水平方向上。因此,上坡/下坡方向正交于平面与f(x,y)的交线。
偏导数的定义:
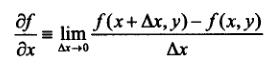
梯度向量为是求偏导?
解:曲面在(x,y)处的高度为f(x,y),是指在(x,y)附近的足够小区域内,认为曲面是局部平坦的。
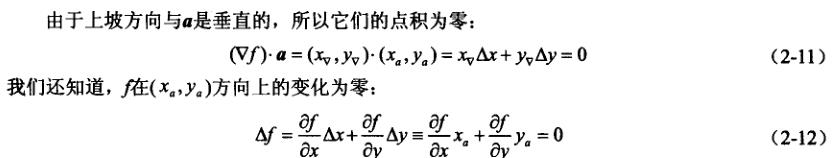




以上是关于虎书学习笔记3:图形学基础数学(正交基与坐标系二维梯度)的主要内容,如果未能解决你的问题,请参考以下文章
虎书学习笔记4:图形学基础数学(隐式二维直线隐式二次曲线二维参数曲线二维参数直线二维参数圆)
机器学习|数学基础Mathematics for Machine Learning系列之矩阵理论:标准正交基与Gram-Schmidt过程