leetcode 1438. 绝对差不超过限制的最长连续子数组----双指针篇3，滑动窗口篇2

Posted 2021-06-01 大忽悠爱忽悠

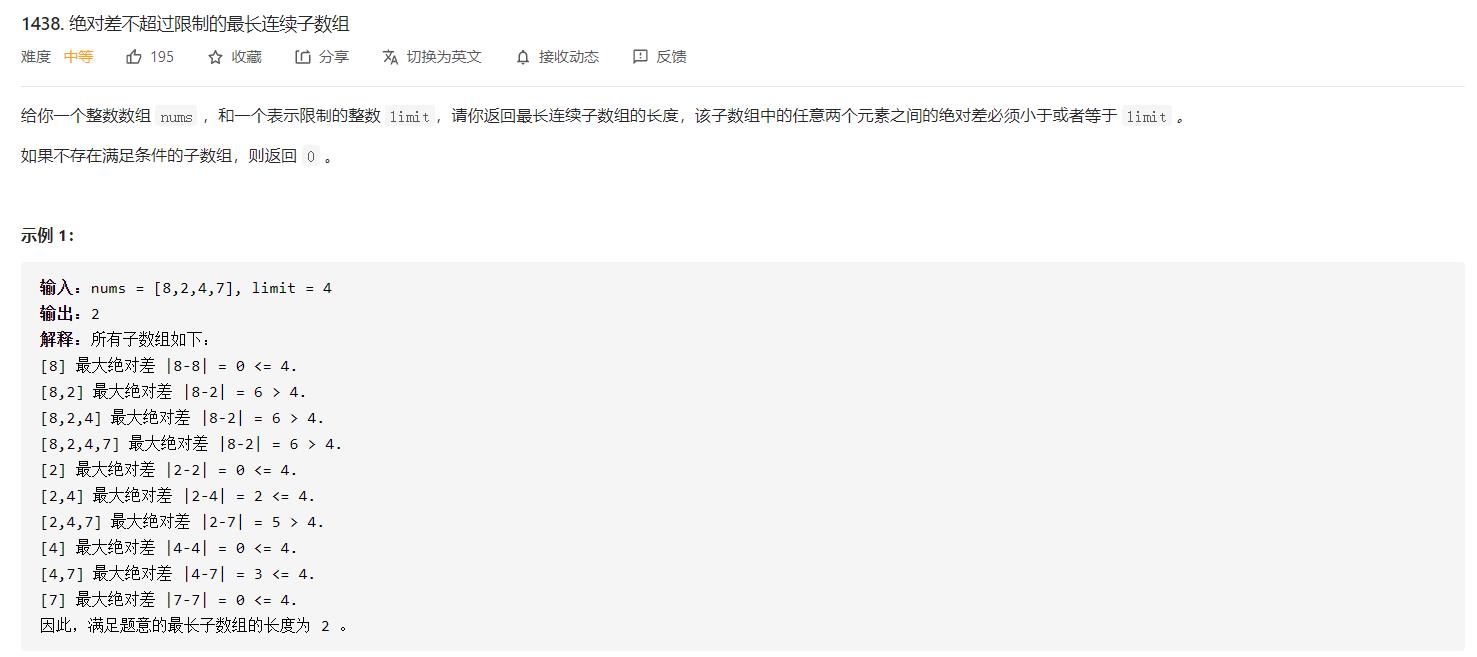
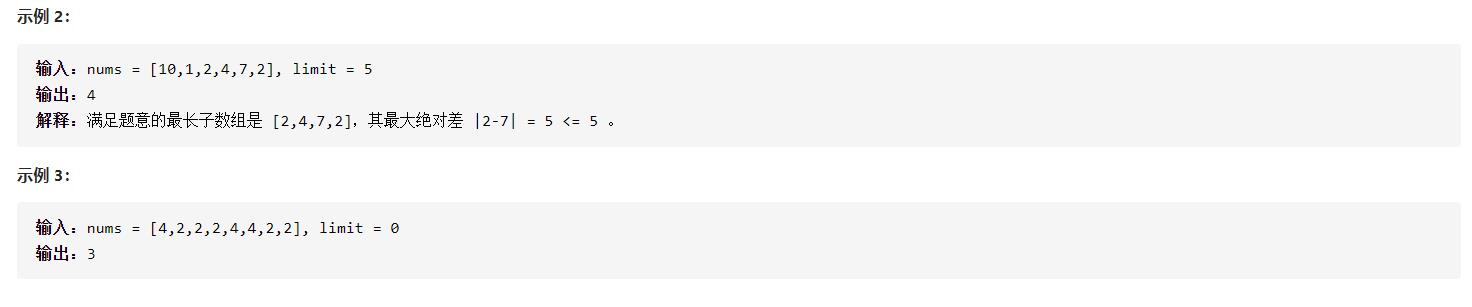
绝对差不超过限制的最长连续子数组题解集合

• 暴力法
• 滑动窗口和双指针
• 利用单调队列找出当前滑动窗口的最大最小值
• 单调队列的优化思路
• 总结

---

暴力法

思路:列举出所有满足条件的子数组，从中找出最大的长度

代码:

class Solution {
public:
	int longestSubarray(vector<int>& nums, int limit) 
	{
		if (nums.empty()) return 0;
		if (nums.size() == 1) return 1;
		int maxLen = 0;
		for (int i = 0; i < nums.size()-1; i++)
		{
			for (int j = 1; j < nums.size(); j++)
			{
				//如果从当前i开始到j结束的连续子数组中出现了绝对差大于限制值的，那么再往后面继续扩大子数组范围也没有意义了
				//found标志记录当前子数组里面有么有任意两个元素的绝对值之差不满足条件
				bool found = false;
				for (int k = i; k < j; k++)
				{
					//一旦找到了一对不满足的例子，就设置标志为真，然后退出当前循环
					if (abs(nums[j] - nums[k]) > limit)
					{
						found = true;
						break;
					}
				}
				//如果找到了不满足的例子，那么从当前i开始的连续子数组就不需要继续往后面扩充长度了，直接从下一个i开始找子数组
				if (found)
					break;
				//能够走到这里说明当前连续子数组满足条件
				maxLen = max(maxLen, j - i+1);
			}
		}
		return maxLen;
	}
};

---

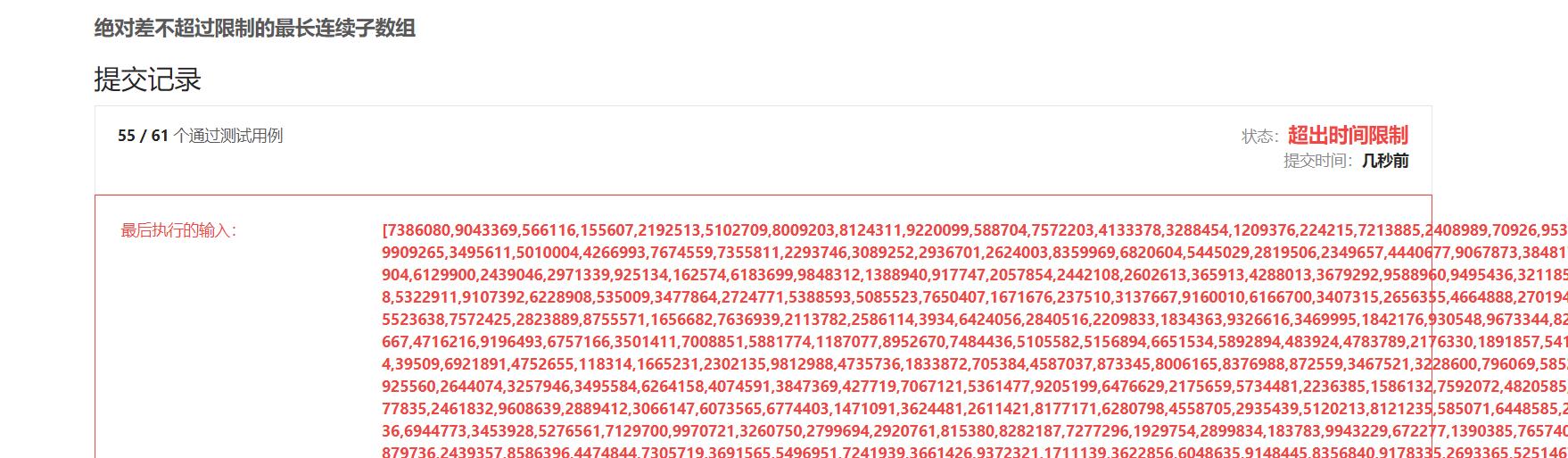
滑动窗口和双指针

思路:

1. 使用滑动窗口保持符合条件的子数组，记录最长长度

2. 怎样确定子数组是否符合条件，需要知道两个关键数据

   21. 子数组中的最大值

   22. 子数组中的最小值

3. 需要对滑入窗口的数据记录，滑出的数据删除，并且使这些记录方便的算出最大值和最小值

   31. 使用 map / multiset 可以在滑入滑出的时候方便的增减对应数据
   32. 同时 map / multiset 本身是有序的，可以方便的找出最大值最小值

4. 这里如果例子是:2,5,3,8,10,11.

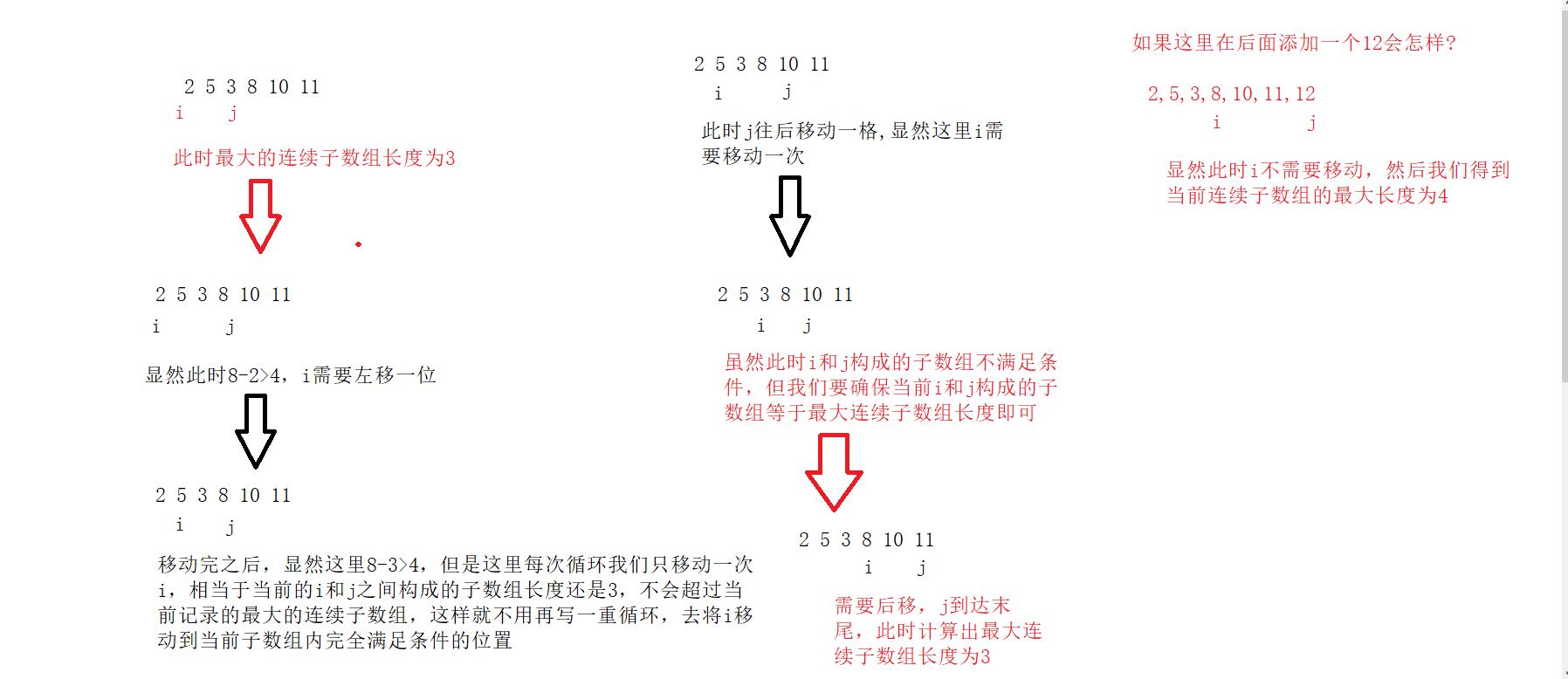
图解:

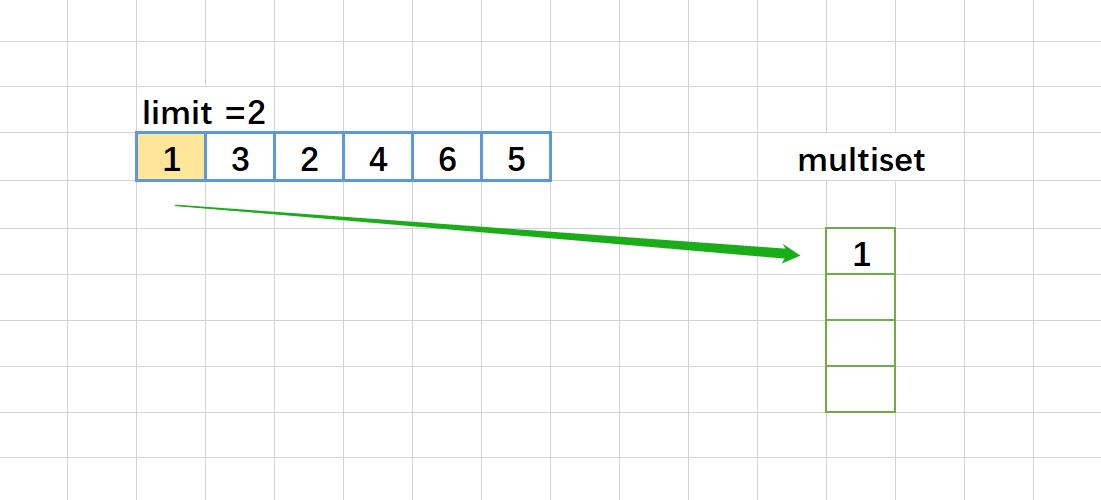
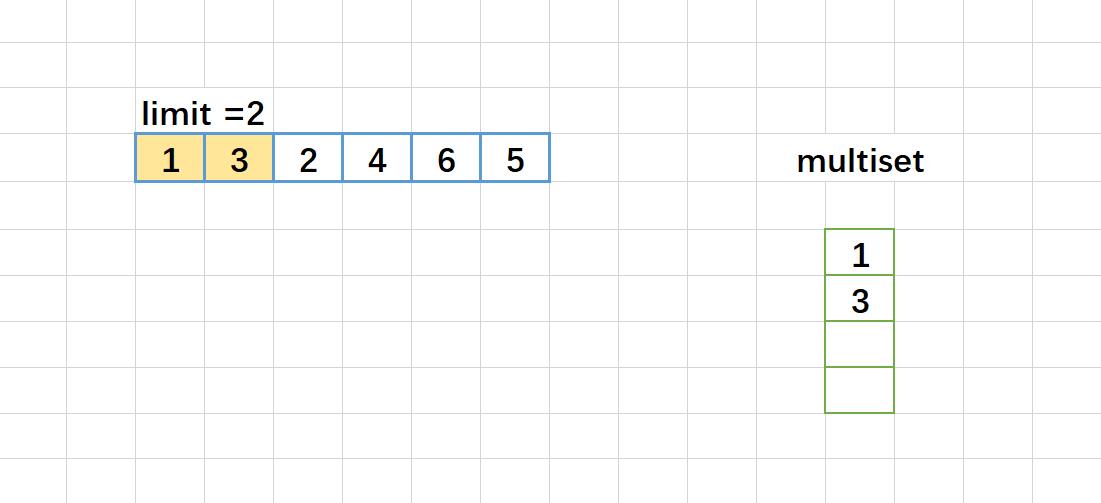
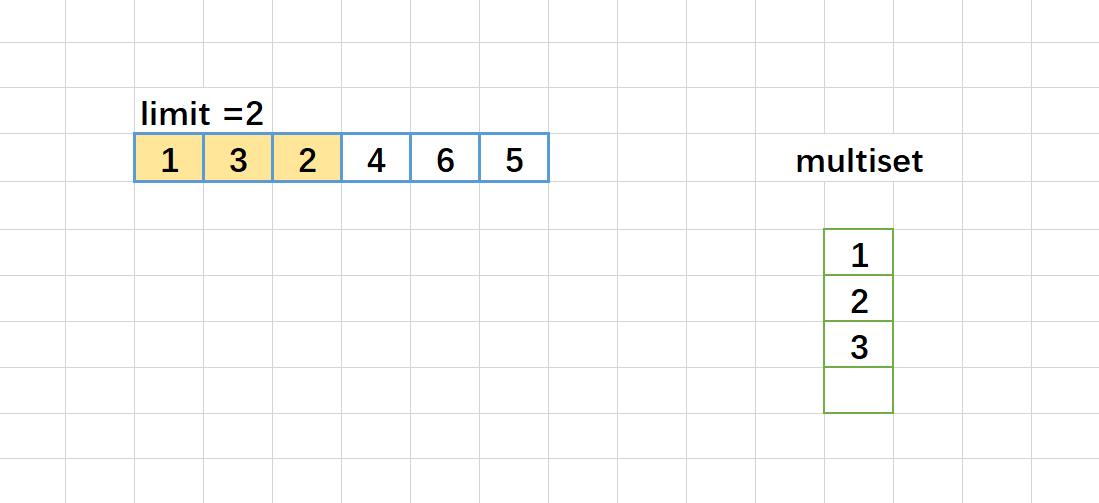
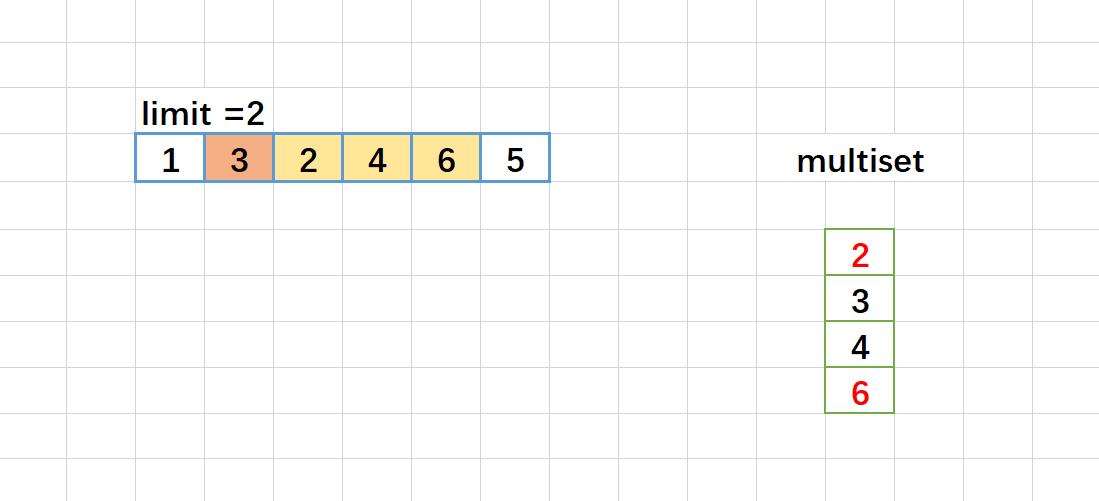
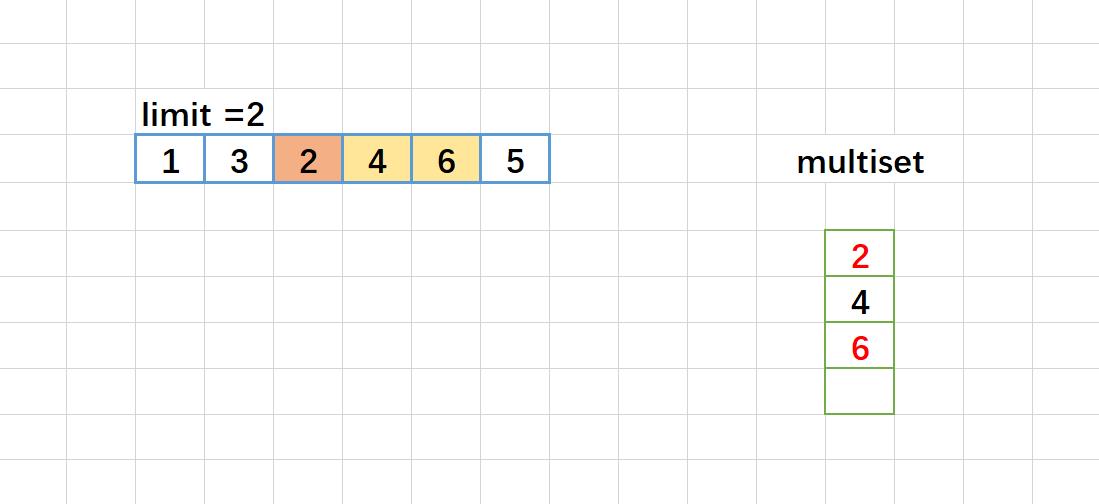
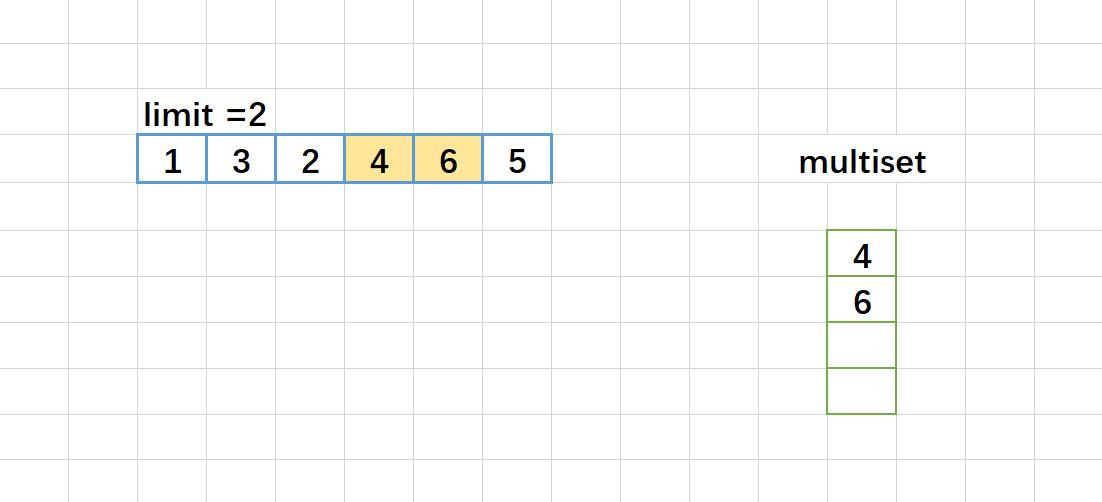
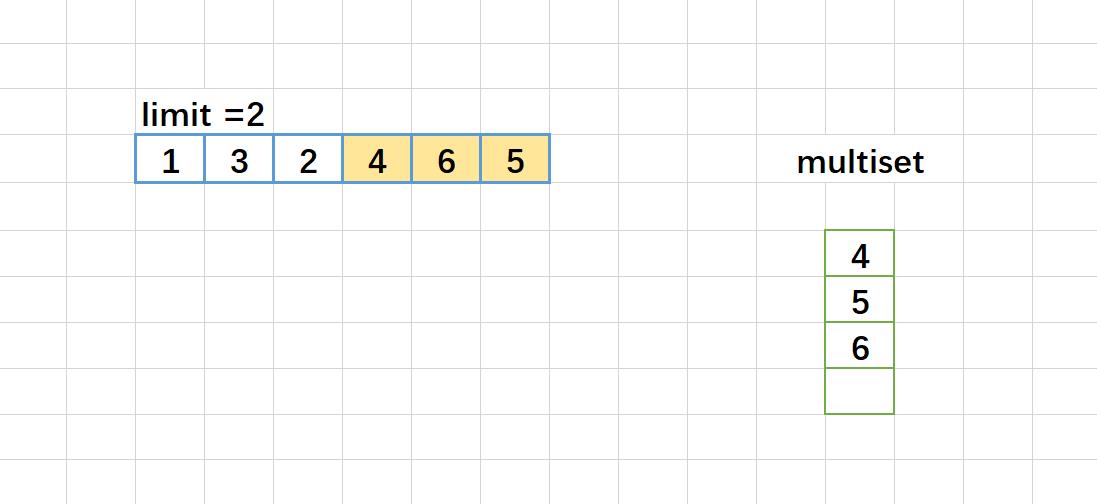
map<int, int> 版本代码:

class Solution {
	map<int, int> m;//关键之是当前元素的值，值是当前元素的出现次数
public:
	int longestSubarray(vector<int>& nums, int limit) 
	{
		if (nums.empty()) return 0;
		if (nums.size() == 1) return 1;
		int maxLen = 0;
		int i = 0;//i指针指向滑动窗口的左端
		for (int j = 0; j < nums.size(); j++)//j指针指向滑动窗口的右端
		{
			m[nums[j]]++;//一开始为0，加1后为1，表示当前元素出现过了一次
			//当前滑动窗口内的最大元素值减去最小元素值不满足条件
			if (m.rbegin()->first - m.begin()->first > limit)
			{
				//将i指针指向的滑动窗口最左端的元素移出

				//这里先将当前元素出现次数减去一，因为这里可能有重复元素
				m[nums[i]]--;
				//判断当前元素的出现次数是否为0，为0的话，直接从map容器中删除
				if (m[nums[i]] == 0)
				{
					//将保存再map容器中的滑动窗口最左端的值删除
					m.erase(nums[i]);
				}
				//i指针往右移动一格，表明将最左端的元素移出窗口
				i++;
			}
			//计算当前滑动窗口的最大长度
			maxLen = max(maxLen, j - i + 1);
		}
		return maxLen;
	}
};

---

这里因为有重复元素，所以使用multiset容器

multiset < int > 版本代码:

class Solution {
	multiset<int> s;//将当前元素的值保存到set容器中
public:
	int longestSubarray(vector<int>& nums, int limit) 
	{
		if (nums.empty()) return 0;
		if (nums.size() == 1) return 1;
		int maxLen = 0;
		int i = 0;//i指针指向滑动窗口的左端
		for (int j = 0; j < nums.size(); j++)//j指针指向滑动窗口的右端
		{
			s.insert(nums[j]);
			if (*s.rbegin() - *s.begin() > limit)
			{
				s.erase(s.find(nums[i]));
				i++;
			}
			//计算当前滑动窗口的最大长度
			maxLen = max(maxLen, j - i + 1);
		}
		return maxLen;
	}
};

注意mutiset删除元素时的小细节:

	multiset<int> set;
	set.insert(1);
	set.insert(4);
	set.insert(3);
	set.insert(2);
	set.insert(5);
	set.insert(3);
	for_each(set.begin(), set.end(), [](int cal) {cout << cal << " "; });
	cout << endl;
	set.erase(3);
	for_each(set.begin(), set.end(), [](int cal) {cout << cal << " "; });

如果是erase(3)，会删除所有值为3的元素，因此我们再解题时，要给他一个迭代器，要他删除找到的第一个重复元素:

s.erase(s.find(nums[i]));

---

利用单调队列找出当前滑动窗口的最大最小值

思路:

1. 创建两个双端队列queue

2. 这两个双端队列一个为单调增队列，一个为单调减队列，即单调增队列中元素的值是递增的，单调减队列中元素的值是单调递减的

3. 当滑动窗口右端要新加入一个元素的时候，分别放入单调增和单调减队列中，怎么放入呢?
   3.1放入单调增队列: 如果当前放入元素比单调增队列的队尾元素还要大，就把队尾元素依次出队，直到前面的元素比当前要放入的元素大为止
   3.2放入单调减队列:如果当前放入的元素比单调减队列的队尾元素还要小，就把队尾元素依次出队，直到前面的元素比当前要放入的元素小为止

4. 以上的步骤可以保证单调增队列的首元素永远是当前滑动窗口的最大值，单调减队列的首元素是当前滑动窗口的最小值

5. 如果当前滑动窗口内的最大值减去最小值得到的结果比限制值要大，那么就需要将滑动窗口的左端值移出滑动窗口，然后继续判断最当前滑动窗口最大值减去最小值是否大于限制值，如果大于就重复第五步

代码:

class Solution {
	deque<int> Min;//单调增队列
	deque<int> Max;//单调减队列
public:
	int longestSubarray(vector<int>& nums, int limit) 
	{
		if (nums.empty()) return 0;
		if (nums.size() == 1) return 1;
		int maxLen = 0;
		int i = 0, j = 0;
		while (j < nums.size())
		{
			int num = nums[j];//获取当前要加入滑动窗口的元素
			while (!Min.empty() && Min.back() > num)
				Min.pop_back();
			Min.push_back(num);
			while (!Max.empty() && Max.back() < num)
				Max.pop_back();
			Max.push_back(num);
			//让滑动窗口左端指针移动到当前滑动窗口内的子数组满足题目要求为止
			while (Max.front() - Min.front() > limit)
			{
                //这里我们需要把左端指针i移动到最大值和最小值两者中下标靠前的后面一个为止即可
				//并且将对应下标靠前的那个从对应的队列首元素中移出
				if (nums[i] == Max.front())
					Max.pop_front();
				else if (nums[i] == Min.front())
					Min.pop_front();
					i++;
			}
			maxLen = max(maxLen, j - i + 1);
			j++;
		}
		return maxLen;
	}
};

---

单调队列的优化思路

思路:

参考滑动窗口和双指针解法，这里只需要确保在未找到更大连续子数组长度的时候，滑动窗口的大小等于当前最长连续子数组长度

做法:

//判断当前i指向位置的元素是否是当前滑动窗口内的最大值或者最小值，如果是就将其从对应的队列中移出即可

代码:

class Solution {
	deque<int> Min;//单调增队列
	deque<int> Max;//单调减队列
public:
	int longestSubarray(vector<int>& nums, int limit) 
	{
		if (nums.empty()) return 0;
		if (nums.size() == 1) return 1;
		int maxLen = 0;
		int i = 0, j = 0;
		while (j < nums.size())
		{
			int num = nums[j];//获取当前要加入滑动窗口的元素
			while (!Min.empty() && Min.back() > num)
				Min.pop_back();
			Min.push_back(num);
			while (!Max.empty() && Max.back() < num)
				Max.pop_back();
			Max.push_back(num);
			if (Max.front() - Min.front() > limit)
			{
				//判断当前i指向位置的元素是否是当前滑动窗口内的最大值或者最小值，如果是就对应的队列中移出即可
				if (nums[i]==Max.front())
					Max.pop_front();
				else if(nums[i]==Min.front())
					Min.pop_front();
					i++;
			}
			maxLen = max(maxLen, j - i + 1);
			j++;
		}
		return maxLen;
	}
};

---

总结

本题的重点在于快速求滑动窗口内的最大值和最小值。常见的方法有：

• 使用 multiset、TreeMap等数据结构；
• 单调递增队列或者单调递减队列；