2021 年 五一数学建模比赛 B 题(第四问至第六问)
Posted zhuo木鸟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021 年 五一数学建模比赛 B 题(第四问至第六问)相关的知识,希望对你有一定的参考价值。
本人专挑数据挖掘、机器学习和 NLP 类型的题目做,有兴趣也可以逛逛我的 数据挖掘竞赛专栏。
如果本篇博文对您有所帮助,请不要吝啬您的点赞 😊
赛题官网:http://51mcm.cumt.edu.cn/
第四问
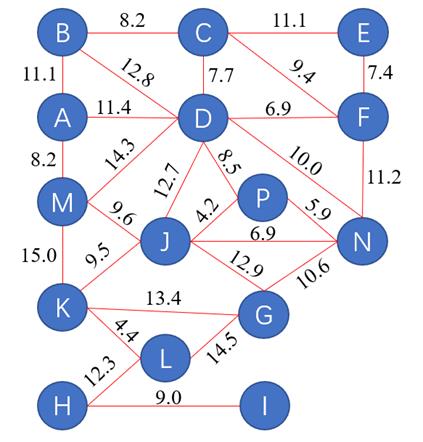
题目是找出不同区域,相关性最高的事件。我们首先整理出事件类型-事件发生密度表格,如下所示:

什么是相关性,我觉得有两个理解:
- 相关性是否指:事件对区域而言呢?也就是找出,该区域某事件发生的密度,在其他区域时,发生密度相差很大的事件,可否如此理解?
- 相关性是否指:事件-事件呢?也就是,不同区域,事件 A 和事件 B 的相关性最大,找出 A 和 B 呢?
第一理解
对于第一个理解,可以沿着上表的行,求出事件的方差,方差最大的那个,就是啦。求出方差如下:
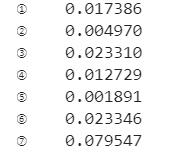
于是,事件 7 是不同区域相关性最大的。
第二理解
第二个理解,沿着行,求出数据的相关性矩阵,找出最大的那个相关性,对应的两个事件,就是啦。
计算偏相关矩阵(使用Pearson相关系数),偏相关系数可以删除其他因素的影响,所以使用偏相关系数:
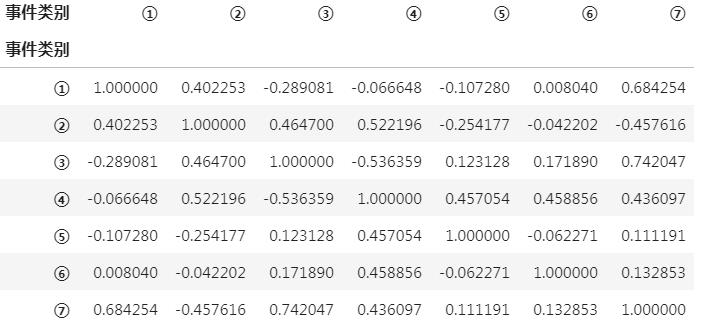
从上图可以找出,事件 3 和 事件 7 在不同区域的相关性最高。
第五问
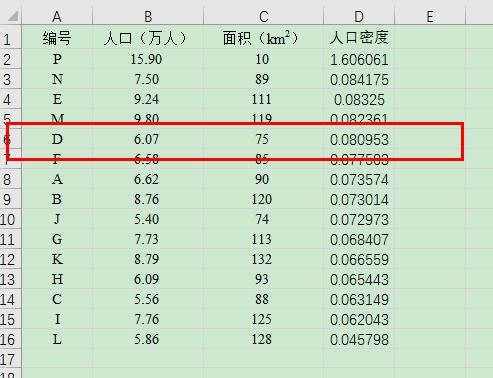
找出人口密度和事件密度的关系,首先就得统计出数据咯:

其中事件密度是根据 16-20 年的总数据算出来的。
如何找出关系呢?还记得问题二的方法吗?
我们首先画出数据:
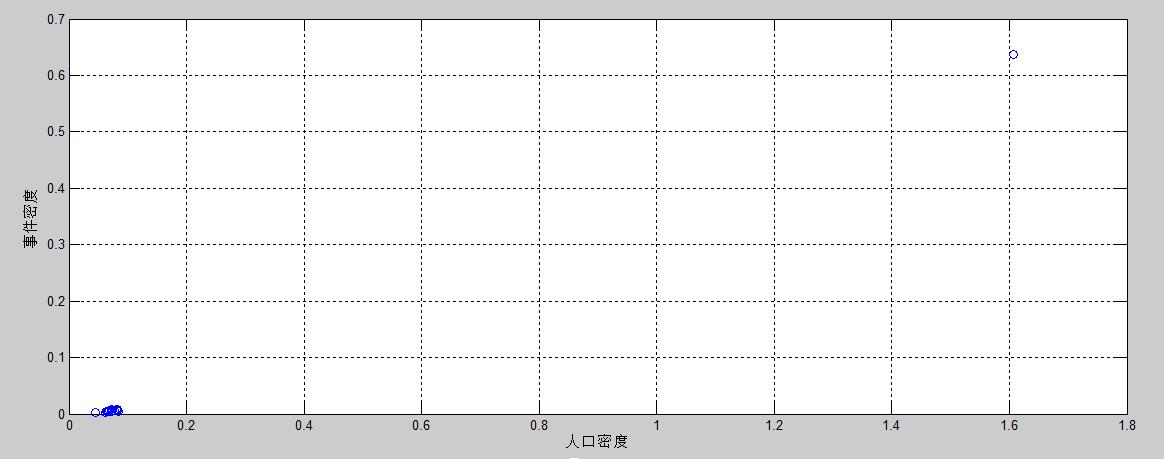
大致可以猜测出,人口密度越大,事件密度(16-20年)越大。
采用第二问的一元回归方法,用线性函数去拟合数据,可得:
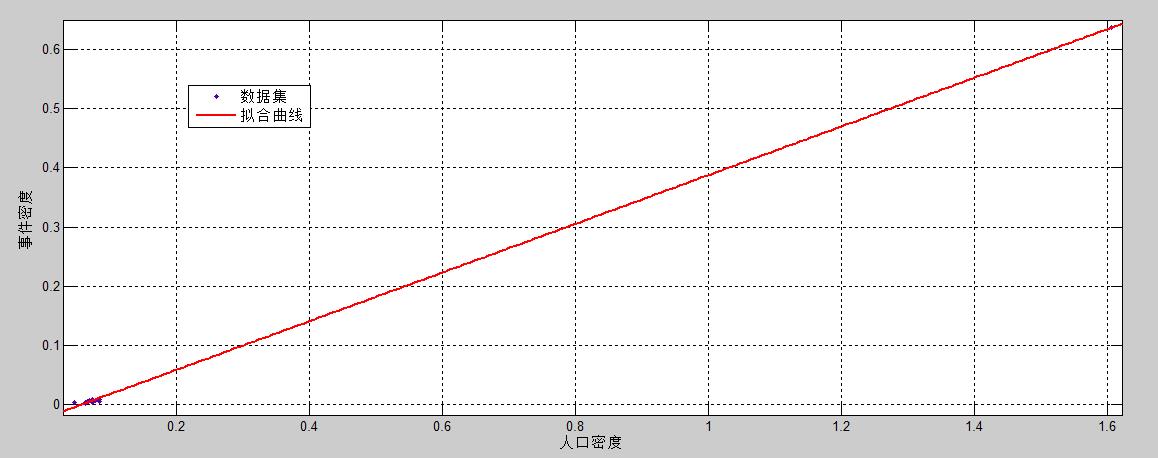
我们可以用 R 方来评价模型的效果,计算出模型的 R 方为:0.9996,可见模型的效果很好。
于是,人口密度和事件密度(16-20): y = 0.4116 x − 0.02374 y=0.4116 x - 0.02374 y=0.4116x−0.02374
第六问
第六问是:
目前该地有两个消防站,分别位于区域J和区域N,请依据附件1和附件2,综合考虑各种因素,建立数学模型,确定如果新建1个消防站,应该建在哪个区域?如果在2021-2029年每隔3年新建1个消防站,则应依次建在哪些区域?
从第四问可知,由于人口密度和事件密度呈现线性关系,且是正相关,所以我们只需要考虑人口密度即可。
先看第一问:该地已经有两个消防站,另一个消防站该建在哪里?
我们不妨先考虑简单的:如果没有消防站,那么消防站应该建在哪里?
若没有消防站,那么,我们可以用谷歌的网页排行算法来解决这个问题。具体是:
- 把每一个节点看成网页
- 把边看成是网页到网页的链接,边的权重视为链接的权重
- 把人口密度视为网页的权重
于是:就可以搜索出最重要的网页,也就是,最重要的节点!
那么,边的权重,以及网页的权重,该如何设置呢?
首先得来看看 PageRank 算法的原理:
PageRank 算法
PageRank 算法要求每一个节点的权重之和是 1,权重是为了模拟每个网页被点击的概率(所有网页被点击的概率当然是 1)
PageRank 算法要求每一个节点,散发出的所有边,的权重之和,为 1。
然后,PageRank 的算法如下(篇幅原因,就用专业的语言描述吧):
设每一个节点的权重为 N i N_i Ni, i i i 是节点编号,为了方便,就即为 { 1 , 2 , ⋯ , n } \\{1,2,\\cdots,n\\} {1,2,⋯,n}, n n n 为节点的数量;若 i i i, j j j 存在边,记边的权重为 w i j w_{ij} wij。设收敛标准为:tol,最大迭代步长为:T,当前步长为:t,设权重传递时的损失参数为 α \\alpha α算法如下:
i n i t i a l N i ( 0 ) t = 0 for i in n : for j in w i : N j ( t + 1 ) + = α ⋅ N i ( t ) ⋅ w i j i f t ≤ T : b r e a k w h i l e ∑ ∣ N i ( t − 1 ) − N i ( t ) ∣ ≤ t o l \\begin{aligned} &initial N_i(0) \\\\ &t=0 \\\\ &\\text{for ~ }\\text{i ~ in ~ }n: \\\\ &\\text{~~~~~~~~for ~ }\\text{j ~ in ~ } w_i: \\\\ &\\text{ ~~~~~~~~~~~~~ ~~~~ } N_j(t+1) += \\alpha \\cdot N_i(t) \\cdot w_{ij}\\\\ &if \\text{~~~~}t \\leq T:\\\\ &\\text{~~~~~~~~}break\\\\ &while \\sum|{N_i(t-1)-N_i(t)}|\\leq tol \\end{aligned} initialNi(0)t=0for i in n: for j in wi: Nj(t+1)+=α⋅Ni(t)⋅wijif t≤T: breakwhile∑∣Ni(t−1)−Ni(t)∣≤tol
应用 PageRank
如何应用呢?
首先如何将节点设置为总和为 1?我认为直接将人口密度进行标准化即可。
如何将某节点的边,设置为总和为 1?
当两个点的距离越大时,应该赋予一个较大的权重。因为距离越远,意味着越需要消防站。因此,如某点到 1,2, 3 的距离为 40,50,10,则权重分别为 0.4, 0.5, 0.1;
带入 PageRank 算法,可得结果如下:

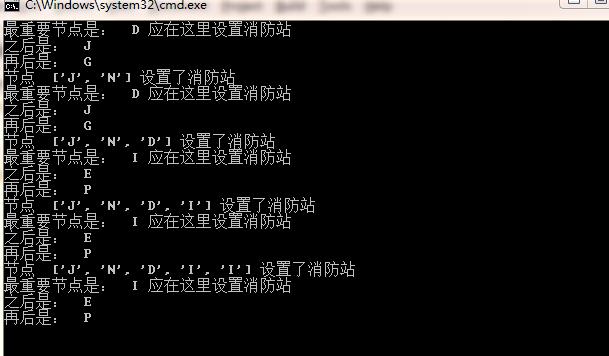
因此,当没有消防站时,最重要的节点是 D。此时应该在 D 中设置消防站。从这个结果来看,还算是比较合理,毕竟 D 节点链接的边最多,而且人口密度也比较多:
J 和 N 设置消防站后
没有设置消防站是,我们用人口密度的标准化,作为节点的权重。
在 J 和 N 设置消防站后,只需要将 J 和 N 的权重设置为 0 即可(或负数,意味着其链接的点的权重也会在迭代过程中下降),这里设置为负数也即,标准化后,J 和 N 的权重为 $ n(w)/15$。其中 n ( w ) n(w) n(w) 为该节点的边数。
之所以设置为 − 2 / 15 -2/15 −2/15,是因为图的节点总数为 15 个,而我们认为一个消防站所起到的扑灭功能,顶的上平均意义上的 n ( w ) n(w) n(w) 个节点权重。当然,这个数值的设置有主观性,it depends。
此时依旧使用 PageRank 算法,可得:

逐年建立消防站(失败的尝试)
因为不知道人口密度的变化,所以按照我们的理论,这是一个静态模型。2021 到 2029 一共 9 年,三年一次,迭代三次。按照上述算法,迭代三次即可:
在运行代码时,我们发现连续三次都需要在 I 中设置消防站,这明显是不合理的。究其原因,就是因为负数在迭代过程中,对周围的线条的影响,超出了我们主观上的预估。
但笔者在将有消防站的节点的权重,设置为 0 时,则出现下面的情况:
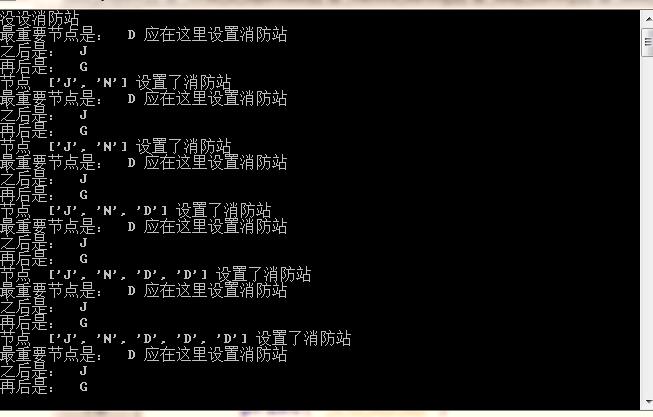
改进方案
本文所讲解的 PageRank 是最简单形式。实际上还有许多复杂的算法。对于设置了消防站的节点,我们可以将其视为悬浮节点,也即对所有节点都看成有链接,且链接是单向的,并根据距离,设置单独地权重。
至于如何实现,就要看大家啦!
代码与提问
若需要代码,请点赞,关注、私信、说明题目和年份
如果有其他问题,请到评论区留言,私信提问,概不回答。也在此鼓励大家独立思考。
本人不会回访,不互关,不互吹,以及谢绝诸如此类事
以上是关于2021 年 五一数学建模比赛 B 题(第四问至第六问)的主要内容,如果未能解决你的问题,请参考以下文章