2021 年 五一数学建模比赛 B 题(第一问至第三问)
Posted zhuo木鸟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021 年 五一数学建模比赛 B 题(第一问至第三问)相关的知识,希望对你有一定的参考价值。
文章目录
2021 年 五一数学建模比赛 B 题(下半部分)
本人专挑数据挖掘、机器学习和 NLP 类型的题目做,有兴趣也可以逛逛我的数据挖掘竞赛专栏。
如果本篇博文对您有所帮助,请不要吝啬您的点赞 😊
赛题官网:http://51mcm.cumt.edu.cn/
思路
-
第一题:
- 对于第一题,其实只要找出每年2月、5月、8月、11月中第一天的三个时间段,发生的事故次数。然后根据事故次数,按比例分配这 30 个人员即可。 对于 第二题,有两个思路:
-
若将次数-月份中的月份转换为自然数,则可以直接将问题视为一个一元回归问题。对此,本文采用了一元一次回归、一元三次回归、sin 函数求和回归、傅里叶函数回归、高斯求和回归,等多个模型,并考虑这些模型的效果。
:
:第二个思路是:将数据视为时间序列,用滑动窗口法,将数据处理转换为可供监督学习的数据,于是将问题转换为机器学习问题。本文对此,将采用线性回归、SVR、决策树、k近邻算法、随机森林、AdaBoost 实现。
两个思路如下图所示:

-
第三题也有两个思路:
-
首先,第三题说到底也是第二题的延续,只要将某一类型的数据提取出来,构成次数-月份数据,就可以用第二题的思路求解了。 不过这样做,就把第三题当成了一个单元时序预测,也即,不考虑各事件类型发生的耦合关系。
: -
另一种就是考虑各时间的耦合关系,将其转换为多元时序预测问题,然后,一锅端!
:
:另外,第三题与第二题的区别在于,第三题口中的月份,是没有加上年份作为前缀的(个人理解+1)。再者,它不需要测试集来评价模型,只需要模型对整个数据集进行拟合,拟合效果最好即可。换句话说,就是越过拟合越好(个人理解+2)。
第一问
根据附件数据,建立数学模型确定消防队在每年2月、5月、8月、11月中第一天的三个时间段各应安排多少人值班,这个问题,似乎就是考察你对数据的增删改查的能力,特别是查的能力。
如何安排呢?毕竟是第一问,肯定不能复杂。所以,我觉得只要找出 16~20 年2月、5月、8月、11月中第一天的三个时间段中,发生事故的次数,然后根据发生事故的次数安排人数就行了。可以按照比例来安排。
所以,问题的重点就在于如何找出16~20 年2月、5月、8月、11月中**第一天**的三个时间段中,发生事故的次数。
这个就要考验大家的编程能力了,我得出的结论是:
年份:16, 月份:2的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为8
属于第3阶段发生的事故次数为7
年份:16, 月份:5的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:16, 月份:8的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:16, 月份:11的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:17, 月份:2的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:17, 月份:5的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:17, 月份:8的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:17, 月份:11的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:18, 月份:2的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:18, 月份:5的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:18, 月份:8的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:18, 月份:11的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:19, 月份:2的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:19, 月份:5的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:19, 月份:8的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:19, 月份:11的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:20, 月份:2的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:20, 月份:5的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:20, 月份:8的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
年份:20, 月份:11的第一天发生的事故次数:
属于第1阶段发生的事故次数为0
属于第2阶段发生的事故次数为0
属于第3阶段发生的事故次数为0
其实大家只要找出所有年份,2,5,8,11月份第一天发生事故的总次数,然后按照次数比拟分配人员就可以了。
第二问
这个问题可以处理成一个回归问题,或者是一个时序预测问题。
说回归问题的,可以将月份视为 x,如 16 年的 1 月份为是 x = 1 x=1 x=1,17 年的 12 月份是 x = 24 x=24 x=24。将本月份发生的事故数视为 y,建立一个一元回归模型即可。
所以,第二问的难点还是编程问题,即如何找出某月份下,发生事故的总次数(类似于 SQL 的 groupby)。
我们可以每月份发生的事故次数数据:
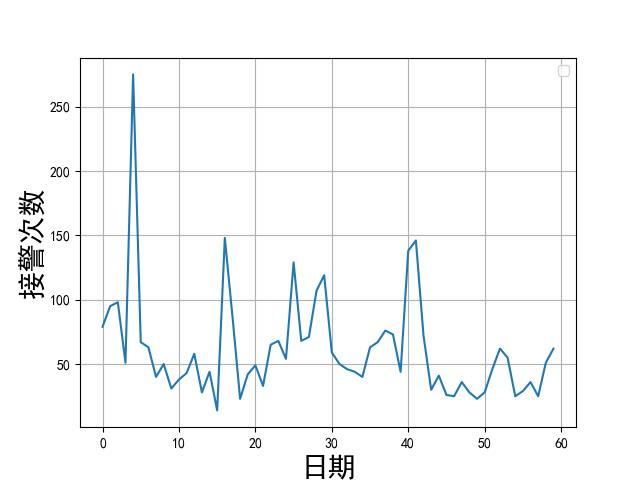
一元回归
如果我们把日期看成自然数序列,似乎就得到了一组(x,y), x ∈ { 1 , 2 , ⋯ , 60 } x\\in\\{1,2,\\cdots,60\\} x∈{1,2,⋯,60}。如何进行一元回归呢?有一个较好的工具是用 MatLab 的 Curve fitting tools。
我们将 2016-2019 年的数据作为训练数据,下面的模型都是在训练集下训练的:
一元多次模型
首先可以用线性回归(首先删除离群值,即发生次数超过 250 的那些数据):
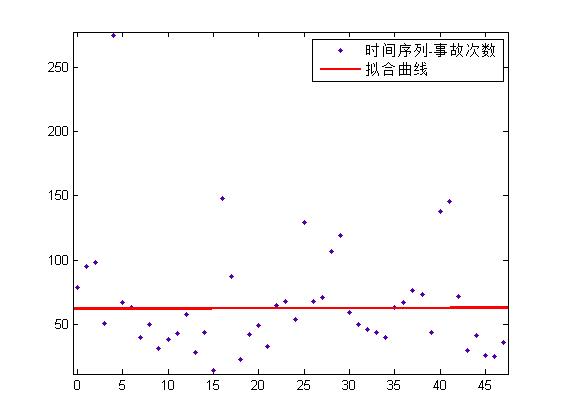
其中
R
M
S
E
=
33.23
RMSE=33.23
RMSE=33.23,(MATLAB 的)
R
M
S
E
RMSE
RMSE 的计算公式如下1:
R
M
S
E
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
RMSE = \\sqrt{\\sum_{i=1}^{n}(x_i-\\bar{x})^2}
RMSE=i=1∑n(xi−xˉ)2
也可以用三元线性回归:
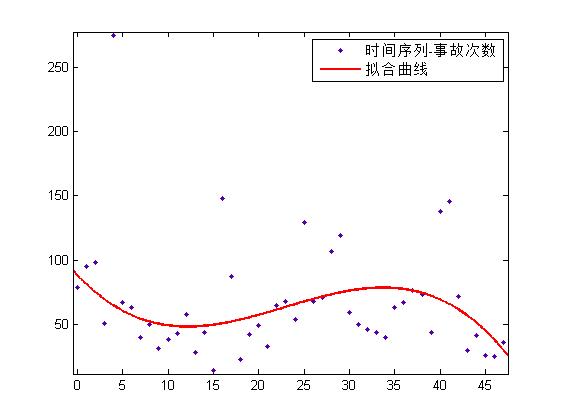
RMSE 为 31.2。
sin 函数累加
也可以用多个 sin 函数累加,来拟合数据,sin 函数累加的模型的表达式如下:
y
=
∑
i
=
1
8
a
i
⋅
sin
(
b
i
⋅
x
+
c
i
)
y = \\sum_{i=1}^{8} a_i\\cdot \\sin(b_i\\cdot x+ c_i)
y=i=1∑8ai⋅sin(bi⋅x+ci)
拟合效果如下所示(训练集),RMSE = 21.44
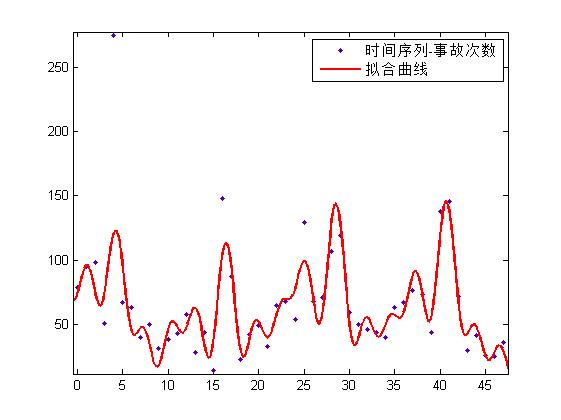
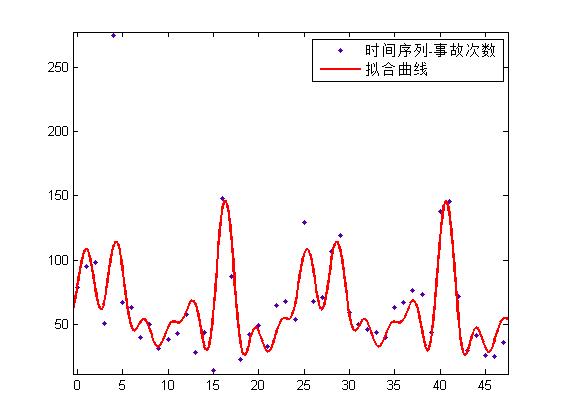
傅里叶函数
我们知道所有的函数都可以转换为一系列正弦、余弦之和,即进行傅里叶分解。所以,我们也考虑用傅里叶函数来拟合数据,表达式如下:
y
=
a
0
+
∑
i
=
1
8
a
i
⋅
cos
(
w
⋅
x
)
+
b
i
⋅
sin
(
w
⋅
x
)
y = a_0 +\\sum_{i=1}^{8} a_i \\cdot \\cos(w\\cdot x) + b_i \\cdot \\sin (w\\cdot x)
y=a0+i=1∑8ai⋅cos(w⋅x)+bi⋅sin(w⋅x)
拟合效果如下(训练集),RMSE=19.93:
高斯函数
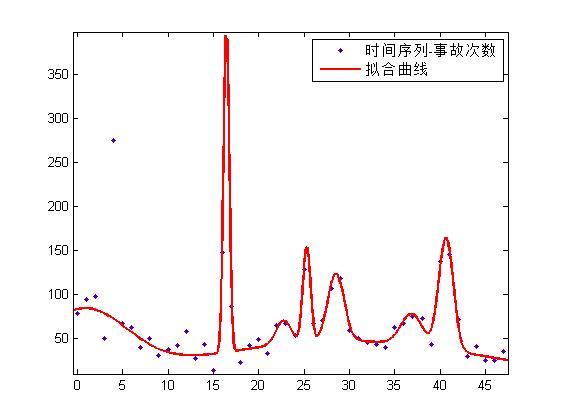
高斯函数是用指数函数去拟合数据,有时也可以取得比较好的效果,高斯函数的表达式如下:
y
=
∑
i
=
1
8
a
i
⋅
exp
(
−
(
x
−
b
i
c
i
)
2
)
y = \\sum_{i=1}^{8} a_i \\cdot \\exp(-(\\frac{x-b_i}{c_i})^2)
y=i=1∑8ai⋅exp(−(cix−bi)2)
拟合效果如下(训练集),RMSE=13.47:
模型评价
上述的模型有一个小问题,就是输出是一个浮点数,因此我们可以在算法实现中,将其输出用四舍五入(np.round)的方法,将输出的浮点数转换为整数。
为了评价模型的效果,我们用 2020 年的数据作为评价数据,用 MSE 作为评价指标,计算公式如下2:
M
S
E
=
∑
i
=
48
59
(
x
i
−
x
ˉ
)
2
n
MSE = \\sum_{i=48}^{59}\\frac{(x_i-\\bar{x})^2}{n}
MSE=i=48∑59n(xi−xˉ)2
可得算出,各模型的 MSE 如下(也太高了吧!):
| 线性回归 | 一元多次 | sin 函数累加 | 傅里叶 | 高斯函数 |
|---|---|---|---|---|
| 776 | 15458 | 1588 | 1467 | 870 |
画出实际数据和拟合数据如下所示:
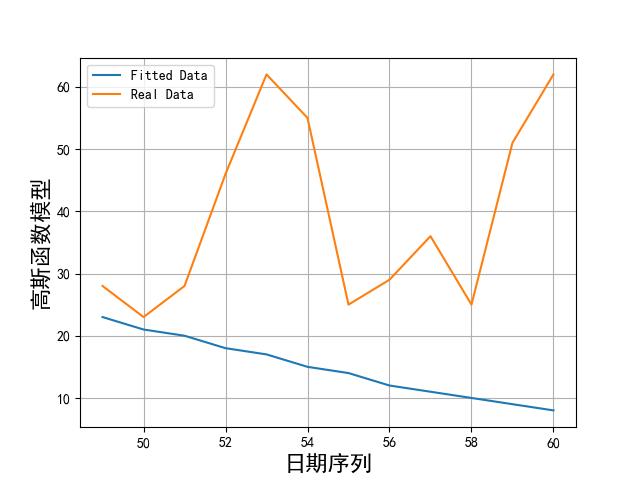
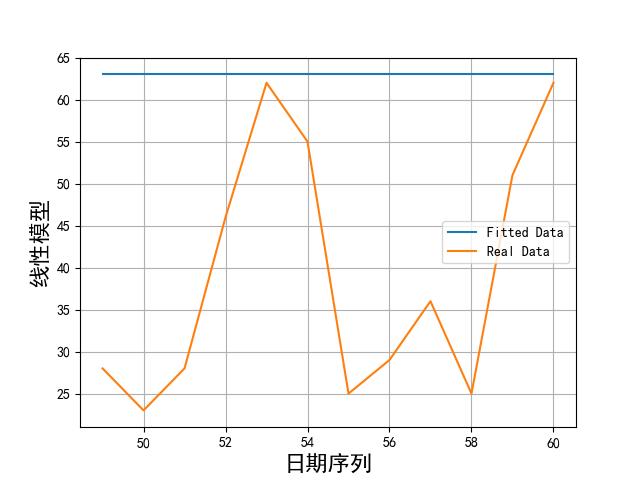
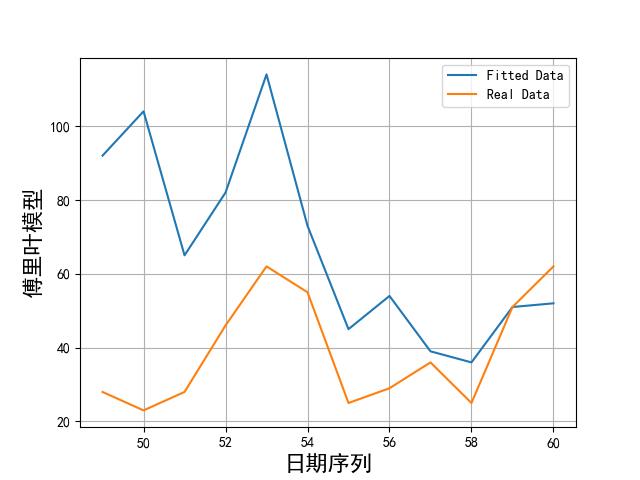
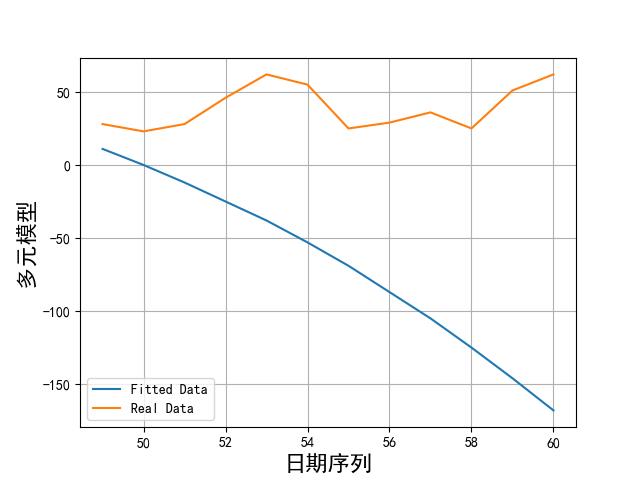
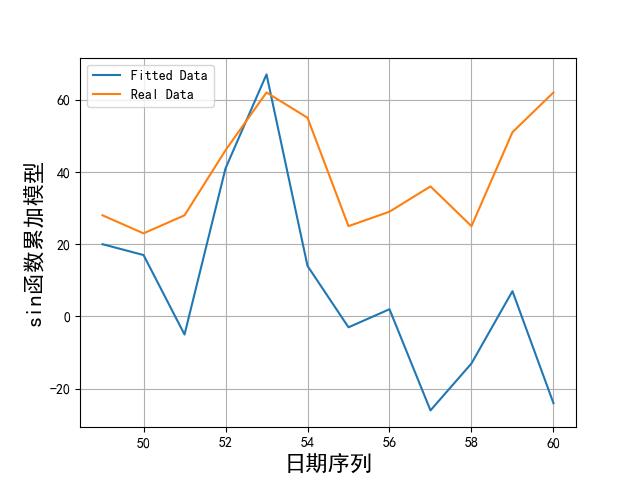
从上述图片可以看到,模型拟合数据和实际数据还是有很大差别的。比较好的模型也就傅里叶和 sin 函数累加了。不过效果这么差,我们就不用在预测了。
时序模型
回归模型和时序模型的一个区别就在于,回归模型仅依据当前状态,对输出进行预测,而没有考虑历史数据。
因此,这里考虑使用时序模型进行解决。但时序模型的实现谈何容易,因此这里用回归模型,去模仿时序模型。如何模仿呢?就要在数据预处理上下功夫。比如,我们用历史数据,作为输入特征,然后将问题转换为机器学习问题。
不过,机器学习对数据量纲比较敏感,所以首先对数据进行均值-方差标准化,即将数据的均值转换为0, 方差为 1。
标准化
标准化后数据如下所示:
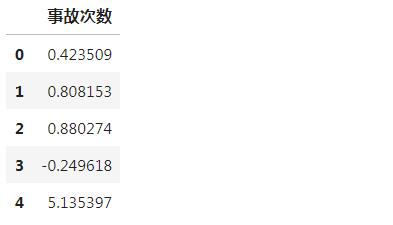
滑动窗口法
为了将历史数据转换为输入特征,我们需要用滑动窗口,设置延迟步长为 5,可得如下:
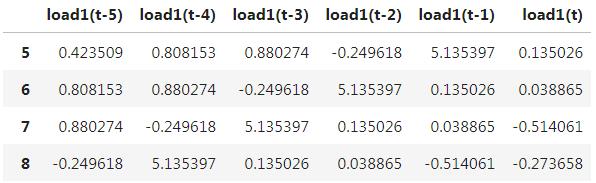
由于头 5 条数据没有足够的延迟,所以,将其直接删除。
机器学习算法搭建预测模型(参数筛选+模型效果)
下面,我们将使用下述算法:
| 算法 | 线性回归 | k近邻算法 | 支持向量机 | 决策树 | 随机森林 | AdaBoost |
|---|---|---|---|---|---|---|
| 符号 | lr | kNN | SVR | dtr | rf | ada |
首先,还是老样子,根据“没有免费午餐”定则,需要筛选模型参数,如何筛选?网格寻优+交叉验证:
定义参数网格如下:
| 算法 | 参数网格 |
|---|---|
| lr | 无 |
| kNN | {‘n_neighbors’:[3,5,7,9,11,13]} |
| SVR | grid = { ‘C’:[0.01, 0.02, 0.05, 0.07, 0.1], ‘kernel’:[‘linear’,‘rbf’,‘poly’], ‘epsilon’: [0, 0.001, 0.05, 0.01, 0.05, 0.1] } |
| dtr | grid = {‘max_depth’:[3, 5, 7, 9], ‘ccp_alpha’:[0,0.01,0.05,0.1,0.2,0.3,0.4,0.5]} |
| rf | 基模型个数:5, 10, 15, 20, 25 |
| ada | 基模型个数:5, 10, 15, 20, 25, 基模型:线性回归 |
定义模型的评价指标为 MSE,最终筛选出模型的最佳参数,以及各大模型的预测效果如下:
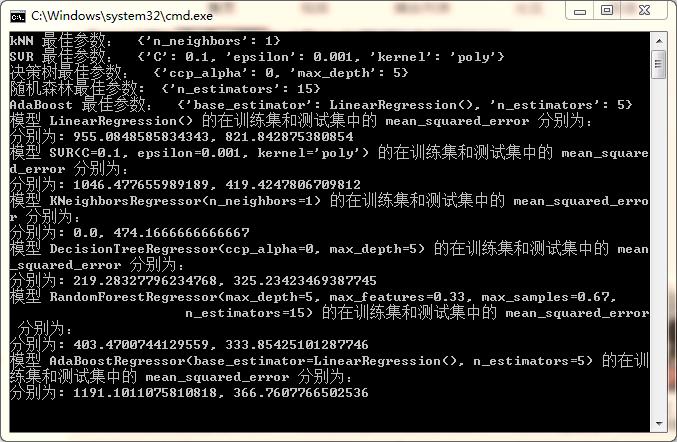
我们也可以画出上述模型在其最优参数下,拟合出来的数据和实际数据的对比图,如下所示:
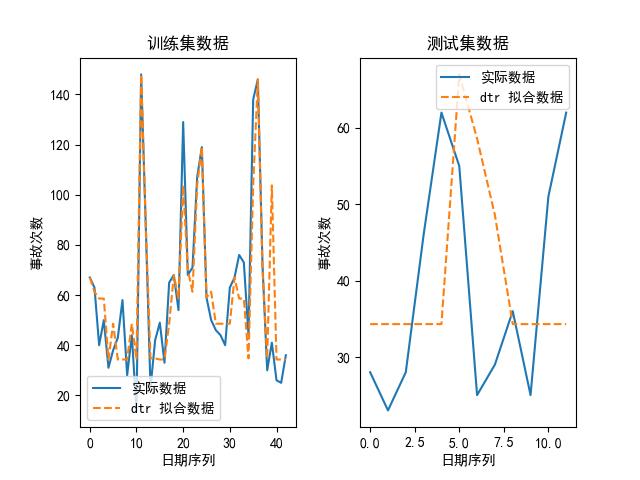
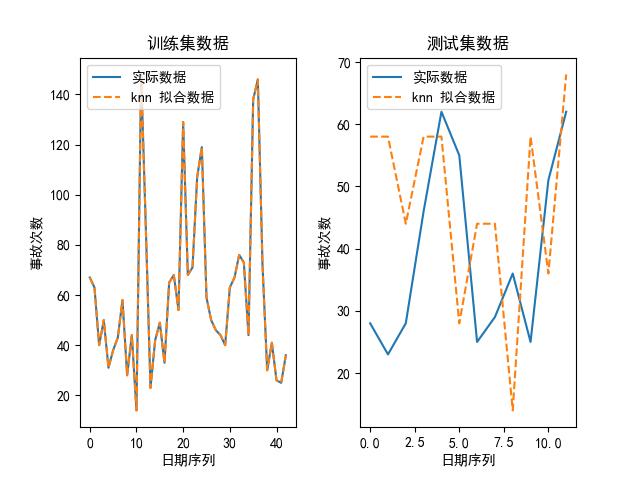
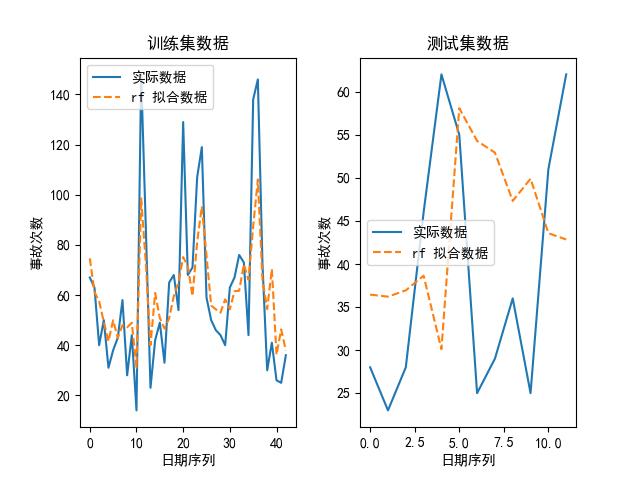
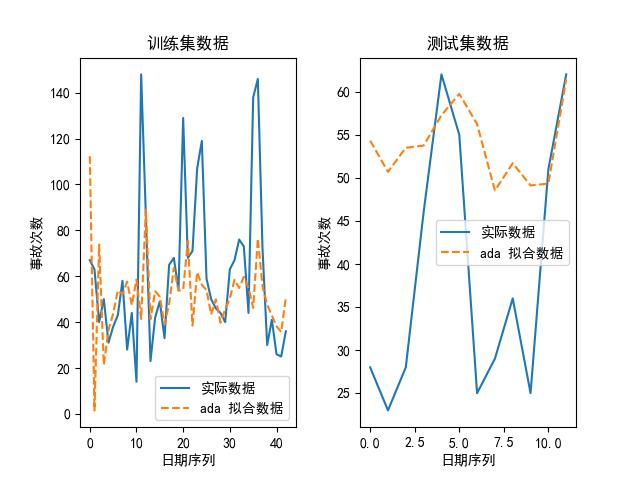
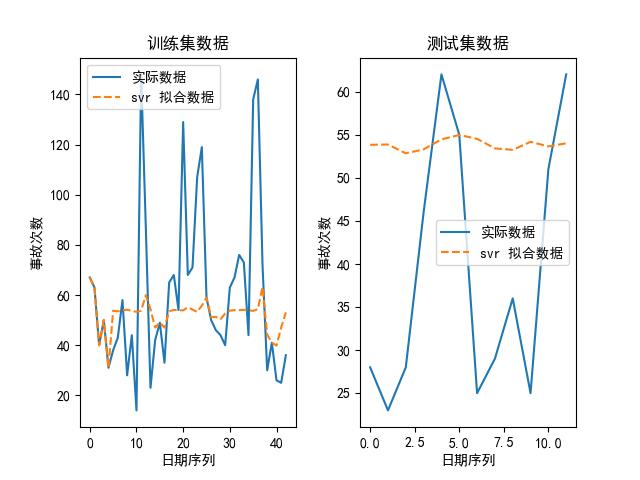
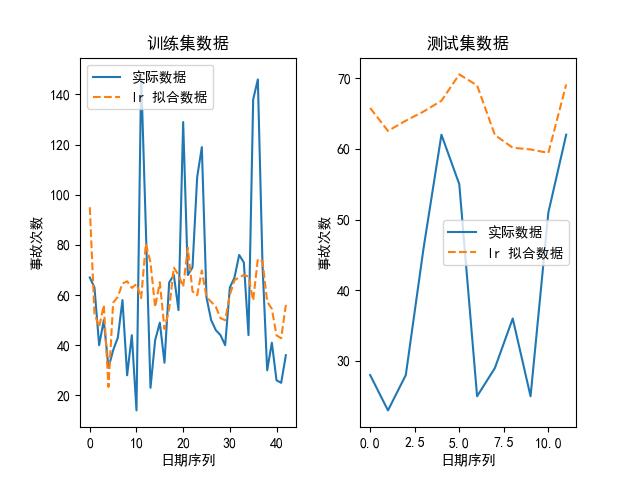
可以看到,随机森林是其中最好的模型。为什么?论精度,它虽然比不上 kNN,但 kNN 的参数是:最大近邻个数为 1,换句话说,它实际上是取原有数据的值取预测未来的值,所以不管用。
另外,我们大致可以预测到的是,随着时代的推移,这些意外事故肯定会降低,所以,考虑到随机森林,一方面其大致的走势与原始数据类似,并且与未来趋势较为匹配,所以选择随机森林作为预测模型吧。
此外:MSE=300+高不高呢?要说高,其实也蛮高的,300 多意味着每一个数据的方差是 300,开一个根号,就是:18 左右。也就是实际报警次数平均下来,比预测的多 18,或者少 18。
随机森林预测次数
用随机森林模型预测出 2021 年的报警次数,如下所示:
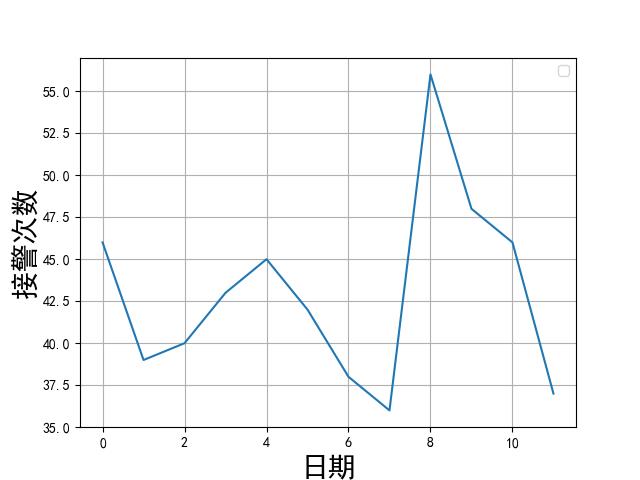
第三问
第三问是要分析,各类事故的次数,和月份的关系了。按我的理解,这里的月份和第二问不同,应该是忽视年份的。所以,对于数据方面,我想应该将统计每一个年份,在16-20年份的发生总次数,作为研究数据。当然,大家也可以采用这 5 年内,每月份发生的,属于特定事件类别的均值,或者用其他统计方法。
所有,第三问和第二问的差别之处:
- 在于首先是范围变小了,第三问是分析指定类别的事故;
- 其次是数据维度缩小了,第三问分析 1-12月,共 12 条数据,而第二问分析 16-20年分别的 1- 12 月份,共 60 条数据。
处理方法的话,可以按照第二问来,即对于每一个类型,我们都把他单独提取出来(单元时序数据)
或者,对于每一个类型,我们统一分析,即多元时序数据。
思路①——单元时序预测
如同思路所示,只需要将某一类型的时间提取出来,构成次数-月份序列,即可完成。因为过程大同小异,我们就以问题类别①为例子,其他的就照猫画虎呗。
数据预处理
首先是均值、方差标准化(这就不展示了),其次是滑动窗口,由于数据较少(才12个),所以就将延迟时间设置为 2:
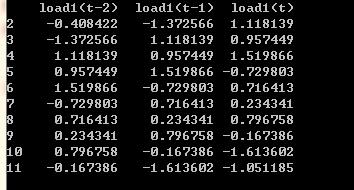
模型搭建(参数筛选+模型效果)
参数筛选
我们将使用以下的算法:
| 算法 | 线性回归 | k近邻算法 | 支持向量机 | 决策树 | 随机森林 | AdaBoost |
|---|---|---|---|---|---|---|
| 符号 | lr | kNN | SVR | dtr | rf | ada |
定义参数网格如下:
| 算法 | 参数网格 |
|---|---|
| lr | 无 |
| kNN | {‘n_neighbors’:[3,5,7,9,11,13]} |
| SVR | grid = { ‘C’:[0.01, 0.02, 0.05, 0.07, 0.1], ‘kernel’:[‘linear’,‘rbf’,‘poly’], ‘epsilon’: [0, 0.001, 0.05, 0.01, 0.05, 0.1] } |
| dtr | grid = {‘max_depth’:[3, 5, 7, 9], ‘ccp_alpha’:[0,0.01,0.05,0.1,0.2,0.3,0.4,0.5]} |
| rf | 基模型个数:5, 10, 15, 20, 25 |
| ada | 基模型个数:5, 10, 15, 20, 25, 基模型:线性回归 |
根据交叉验证,得出结论如下:

模型效果
(根据问题理解,这道题不需要拆分成训练集、测试集)直接将数据投入模型训练,可得各个模型的效果如下:
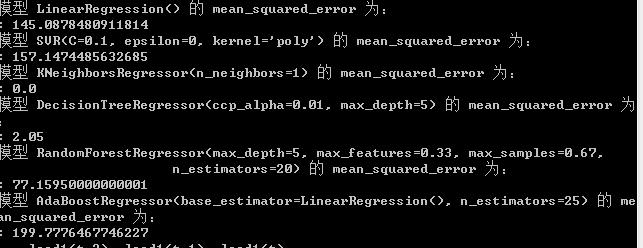
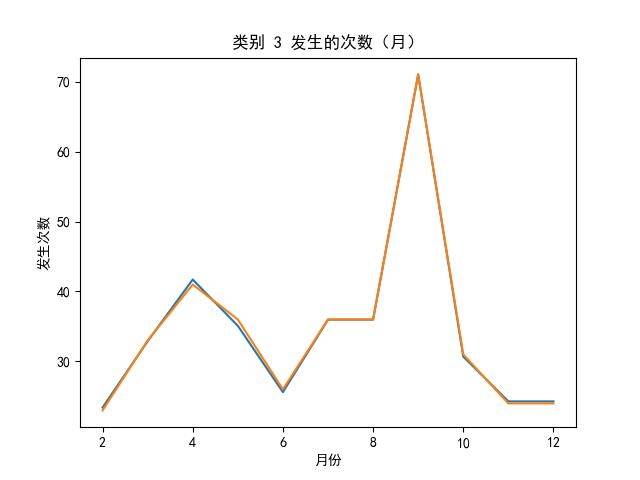
可知,选 knn 算法最好啦,为了直观地展示,我们也可以画出实际数据、拟合数据图:
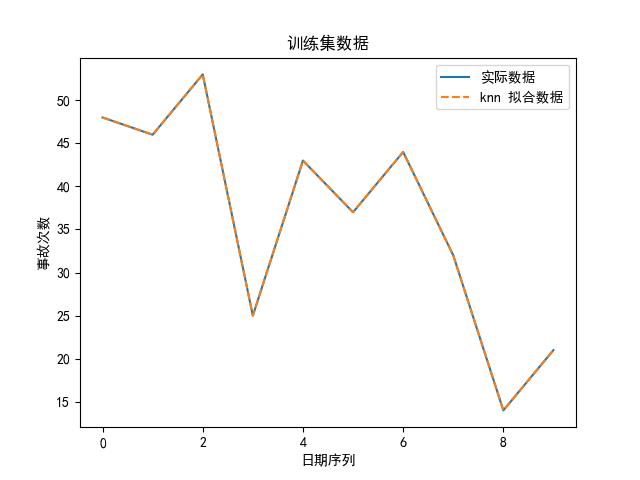
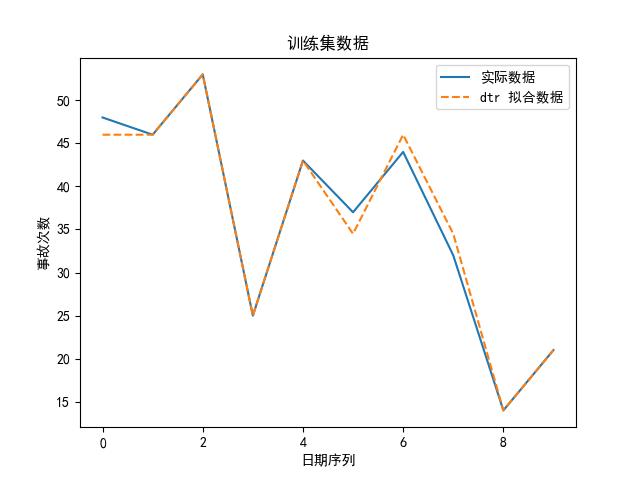
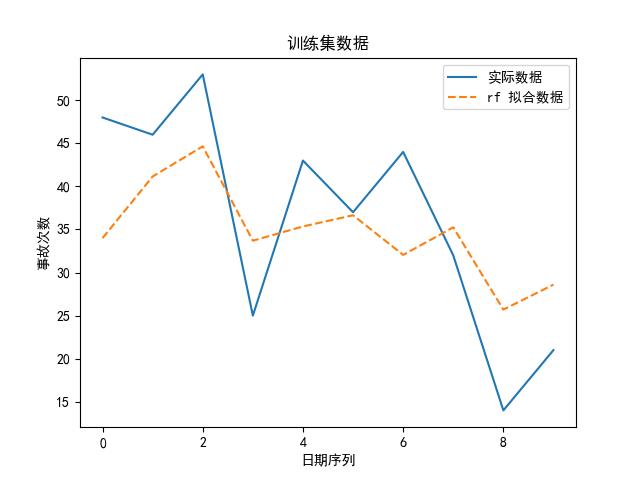

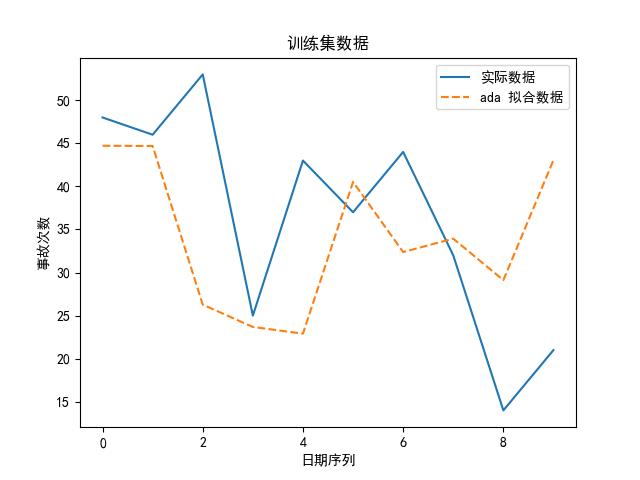
思路②——多元时序预测
首先总结出各类数据月发生次数(总次数),如下表所示:
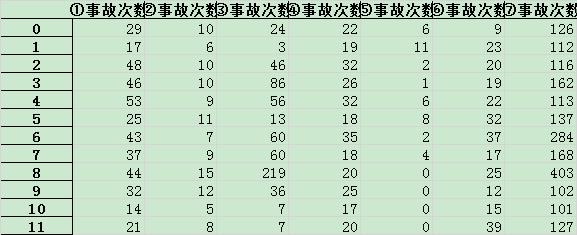
标准化如下:
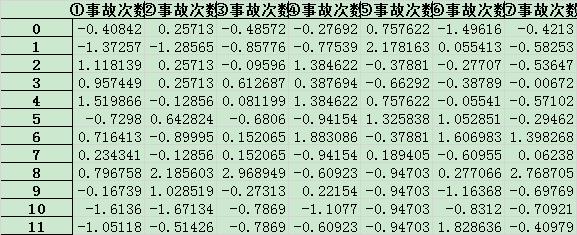
进行窗口滑动后,数据如下(时间延迟为 1):
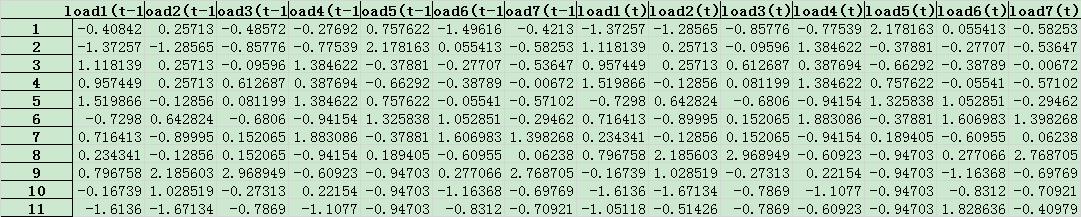
即根据前一天,预测后一天(数据量太少了呀。)
LSTMs 模型
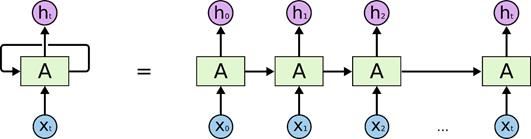
我们使用 LSTMs 时序神经网络模型,来拟合数据(设置循环次数,即图中的 A 为 64 个,训练算法为 Adam),LSTMs 迭代的情况如下:
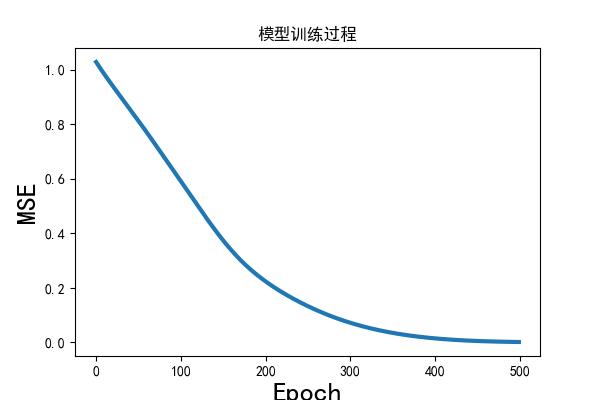
拟合数据和实际数据的 MSE 为(标准化前的):0.25

LSTMs 效果图
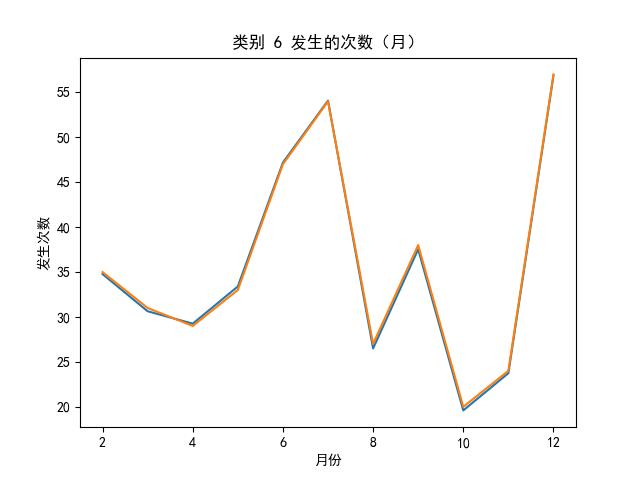
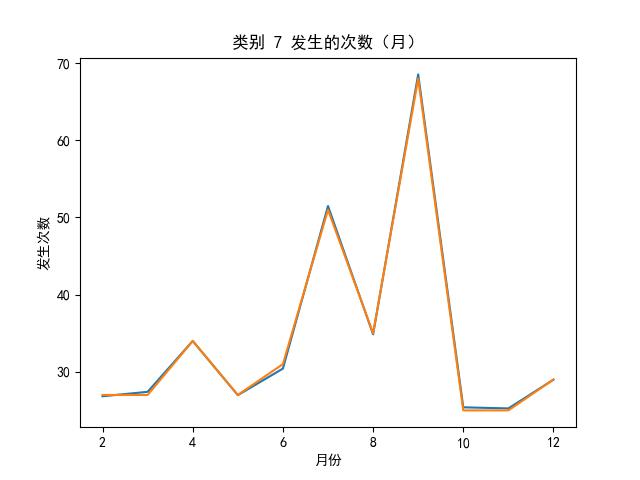
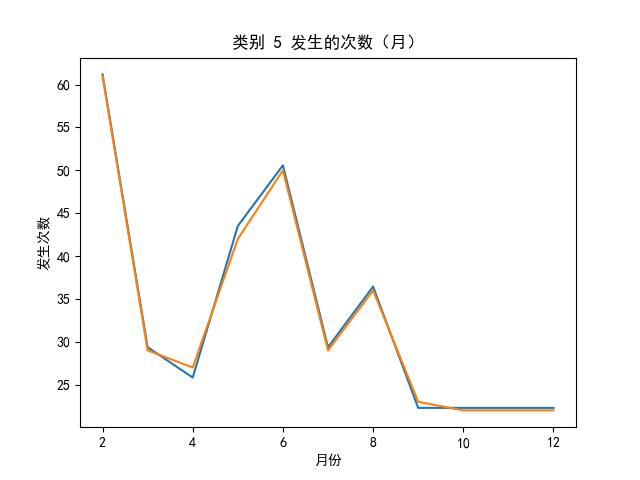
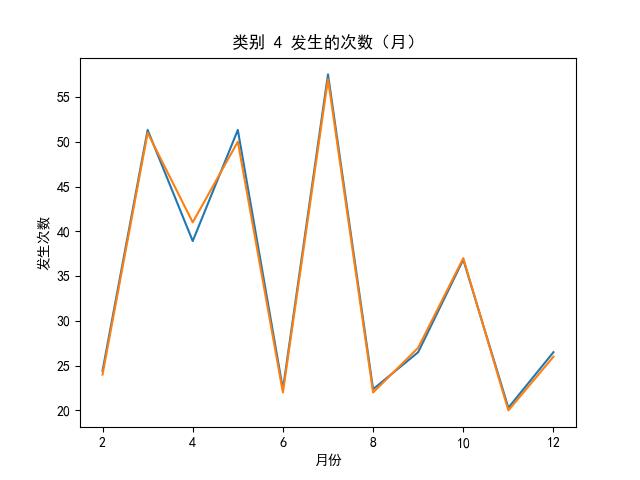
的主要内容,如果未能解决你的问题,请参考以下文章</p>
<p > <a style=) 2021 年 五一数学建模比赛 B 题(第四问至第六问)
2021 年 五一数学建模比赛 B 题(第四问至第六问)