RepVGG：极简架构，SOTA性能，论文解读

Posted 2021-05-29 踟蹰横渡口,彳亍上滩舟。

**

RepVGG：极简架构，SOTA性能，论文解读

**

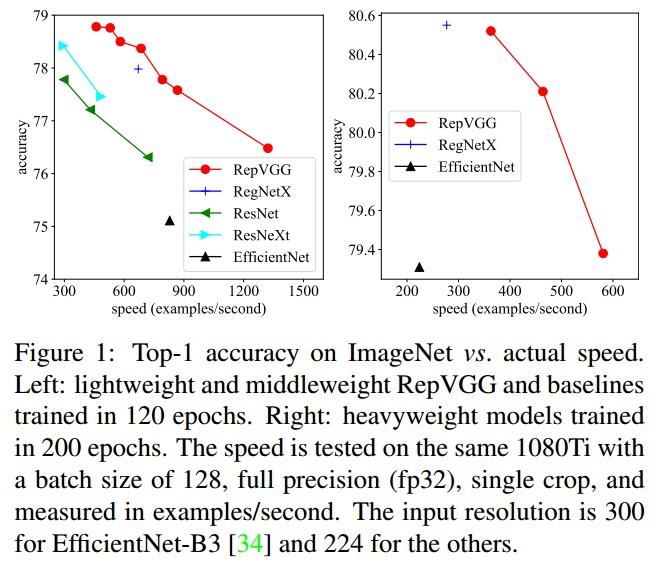
更新：RepVGG的更深版本达到了83.55%正确率！PyTorch代码和模型已经在GitHub上放出。DingXiaoH/RepVGG

2020年B站年度弹幕是“爷青回”。一定有很多瞬间，让你感觉“爷的青春回来了”。在这个卷积网络各种超参精确到小数点后三位的时代，你是否还记得五六年前的田园时代，堆几个卷积层就能涨点的快乐？ ResNet和Inception等模型提出后，大家的研究重点逐渐转向各种多分支卷积网络架构，VGG这样的“直筒型”简单架构鲜有问津。

而我们相信科学技术总是螺旋式地上升。我们捡起七年前的老架构，注入了一个新想法。让七年前的模型再次跟上SOTA，是多么有趣的一件事！

我们最近的工作RepVGG，用结构重参数化（structural re-parameterization）“复兴”VGG式单路极简架构，一路3x3卷到底，在速度和性能上达到SOTA水平，在ImageNet上超过80%正确率。已经被CVPR-2021接收。

不用NAS，不用attention，不用各种新颖的激活函数，甚至不用分支结构，只用3x3卷积和ReLU，也能达到SOTA性能？

论文地址：下载地址

开源预训练模型和代码（PyTorch版）：https://github.com/DingXiaoH/RepVGG。已有1200+ star。除了构建模型、训练、转换的代码以外，也包括一些对常见问题的回答。

（MegEngine版）：下载地址

太长不看版
方法有多简单呢？下午5点看完文章，晚饭前就能写完代码开始训练，第二天就能看到结果。如果没时间看完这篇文章，只要点开下面的代码，看完前100行就可以完全搞明白。https://github.com/DingXiaoH/RepVGG/blob/main/repvgg.py

下面是详细介绍。

模型定义
我们所说的“VGG式”指的是：

1. 没有任何分支结构。即通常所说的plain或feed-forward架构。

2. 仅使用3x3卷积。

3. 仅使用ReLU作为激活函数。

下面用一句话介绍RepVGG模型的基本架构：将20多层3x3卷积堆起来，分成5个stage，每个stage的第一层是stride=2的降采样，每个卷积层用ReLU作为激活函数。

再用一句话介绍RepVGG模型的详细结构：RepVGG-A的5个stage分别有[1, 2, 4, 14, 1]层，RepVGG-B的5个stage分别有[1, 4, 6, 16, 1]层，宽度是[64, 128, 256, 512]的若干倍。这里的倍数是随意指定的诸如1.5,2.5这样的“工整”的数字，没有经过细调。

再用一句话介绍训练设定：ImageNet上120 epochs，不用trick，甚至直接用PyTorch官方示例的训练代码就能训出来！

为什么要设计这种极简模型，这么简单的纯手工设计模型又是如何在ImageNet上达到SOTA水平的呢？

为什么要用VGG式模型
除了我们相信简单就是美以外，VGG式极简模型至少还有五大现实的优势（详见论文）。

1. 3x3卷积非常快。在GPU上，3x3卷积的计算密度（理论运算量除以所用时间）可达1x1和5x5卷积的四倍。

2. 单路架构非常快，因为并行度高。同样的计算量，“大而整”的运算效率远超“小而碎”的运算。

3. 单路架构省内存。例如，ResNet的shortcut虽然不占计算量，却增加了一倍的显存占用。

4. 单路架构灵活性更好，容易改变各层的宽度（如剪枝）。

5. RepVGG主体部分只有一种算子：3x3卷积接ReLU。在设计专用芯片时，给定芯片尺寸或造价，我们可以集成海量的3x3卷积-ReLU计算单元来达到很高的效率。别忘了，单路架构省内存的特性也可以帮我们少做存储单元。

结构重参数化让VGG再次伟大
相比于各种多分支架构（如ResNet，Inception，DenseNet，各种NAS架构），近年来VGG式模型鲜有关注，主要自然是因为性能差。例如，有研究[1]认为，ResNet性能好的一种解释是ResNet的分支结构（shortcut）产生了一个大量子模型的隐式ensemble（因为每遇到一次分支，总的路径就变成两倍），单路架构显然不具备这种特点。

既然多分支架构是对训练有益的，而我们想要部署的模型是单路架构，我们提出解耦训练时和推理时架构。我们通常使用模型的方式是：

1. 训练一个模型

2. 部署这个模型

但在这里，我们提出一个新的做法：

1. 训练一个多分支模型

2. 将多分支模型等价转换为单路模型

3. 部署单路模型

这样就可以同时利用多分支模型训练时的优势（性能高）和单路模型推理时的好处（速度快、省内存）。这里的关键显然在于这种多分支模型的构造形式和转换的方式。

我们的实现方式是在训练时，为每一个3x3卷积层添加平行的1x1卷积分支和恒等映射分支，构成一个RepVGG Block。这种设计是借鉴ResNet的做法，区别在于ResNet是每隔两层或三层加一分支，而我们是每层都加。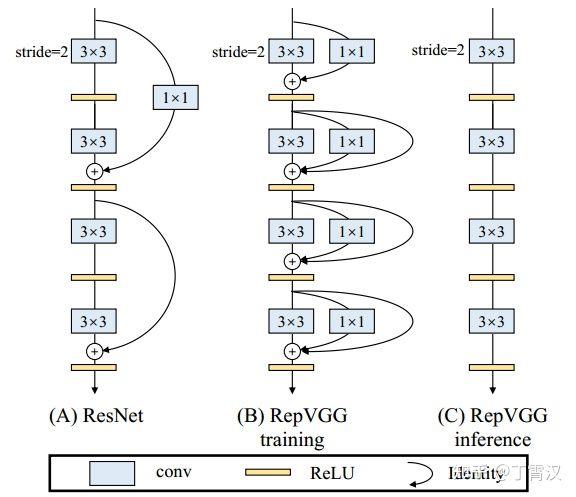
训练完成后，我们对模型做等价转换，得到部署模型。根据卷积的线性（具体来说是可加性），设三个3x3卷积核分别是W1，W2，W3，有 conv(x, W1) + conv(x, W2) + conv(x, W3) = conv(x, W1+W2+W3)）。怎样利用这一原理将一个RepVGG Block转换为一个卷积呢？

其实非常简单，因为RepVGG Block中的1x1卷积是相当于一个特殊（卷积核中有很多0）的3x3卷积，而恒等映射是一个特殊（以单位矩阵为卷积核）的1x1卷积，因此也是一个特殊的3x3卷积！我们只需要：1. 把identity转换为1x1卷积，只要构造出一个以单位矩阵为卷积核的1x1卷积即可；2. 把1x1卷积等价转换为3x3卷积，只要用0填充即可。

下图描述了这一转换过程。在这一示例中，输入和输出通道都是2，故3x3卷积的参数是4个3x3矩阵，1x1卷积的参数是一个2x2矩阵。注意三个分支都有BN（batch normalization）层，其参数包括累积得到的均值及标准差和学得的缩放因子及bias。这并不会妨碍转换的可行性，因为推理时的卷积层和其后的BN层可以等价转换为一个带bias的卷积层（也就是通常所谓的“吸BN”）。

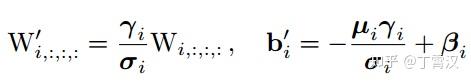
对三分支分别“吸BN”之后（注意恒等映射可以看成一个“卷积层”，其参数是一个2x2单位矩阵！），将得到的1x1卷积核用0给pad成3x3。最后，三分支得到的卷积核和bias分别相加即可。这样，每个RepVGG Block转换前后的输出完全相同，因而训练好的模型可以等价转换为只有3x3卷积的单路模型。

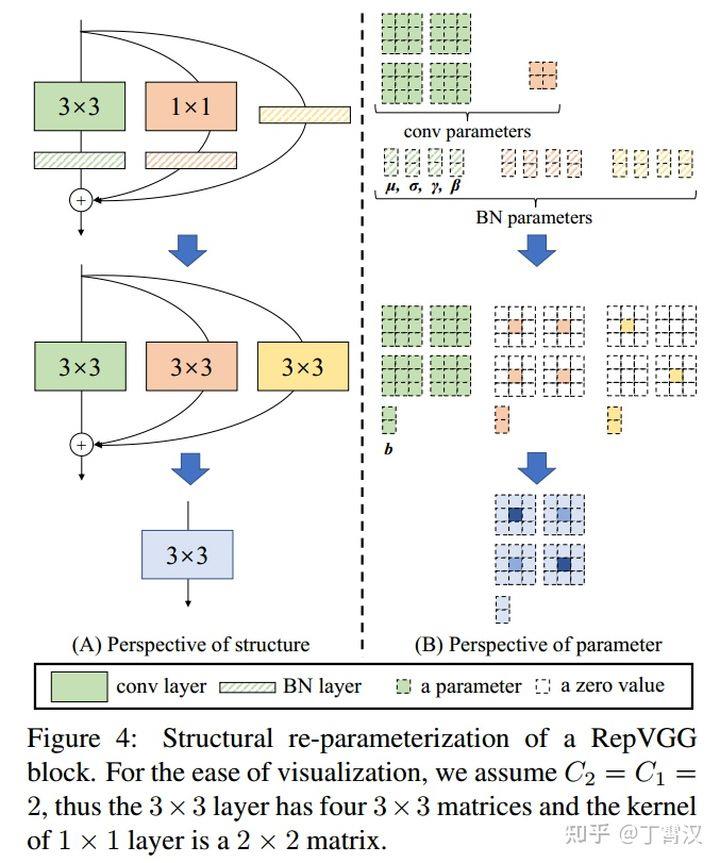
从这一转换过程中，我们看到了“结构重参数化”的实质：训练时的结构对应一组参数，推理时我们想要的结构对应另一组参数；只要能把前者的参数等价转换为后者，就可以将前者的结构等价转换为后者。

实验结果
在1080Ti上测试，RepVGG模型的速度-精度相当出色。在公平的训练设定下，同精度的RepVGG速度是ResNet-50的183%，ResNet-101的201%，EfficientNet的259%，RegNet的131%。注意，RepVGG取得超过EfficientNet和RegNet的性能并没有使用任何的NAS或繁重的人工迭代设计。

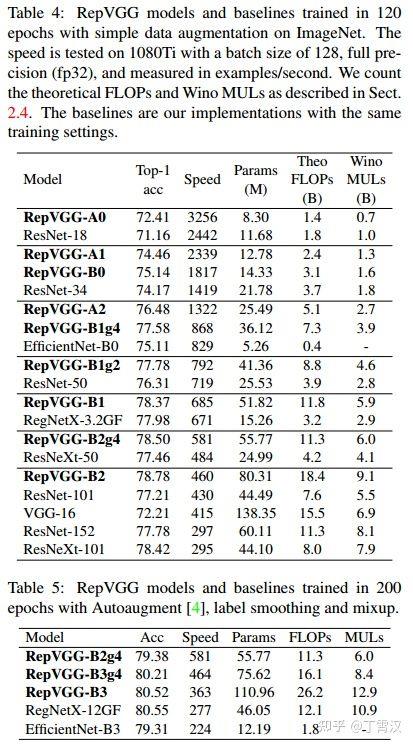
这也说明，在不同的架构之间用FLOPs来衡量其真实速度是欠妥的。例如，RepVGG-B2的FLOPs是EfficientNet-B3的10倍，但1080Ti上的速度是后者的2倍，这说明前者的计算密度是后者的20余倍。

在Cityscapes上的语义分割实验表明，在速度更快的情况下，RepVGG模型比ResNet系列高约1%到1.7%的mIoU，或在mIoU高0.37%的情况下速度快62%。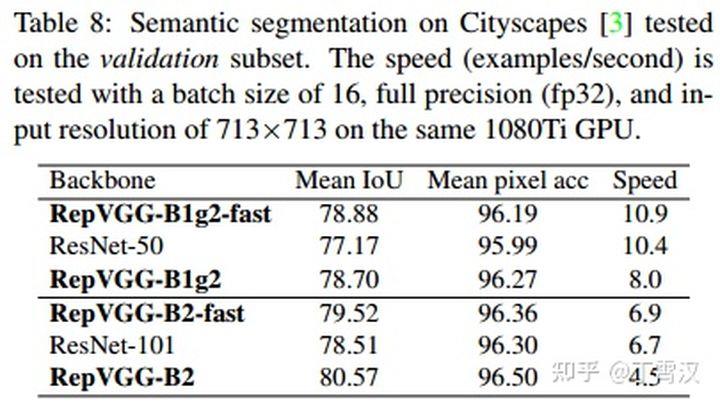
另外一系列ablation studies和对比实验表明，结构重参数化是RepVGG模型性能出色的关键（详见论文）。

最后需要注明的是，RepVGG是为GPU和专用硬件设计的高效模型，追求高速度、省内存，较少关注参数量和理论计算量。在低算力设备上，可能不如MobileNet和ShuffleNet系列适用。

参考文献
[1] Andreas Veit, Michael J Wilber, and Serge Belongie. Residual networks behave like ensembles of relatively shallow networks. In Advances in neural information processing systems, pages 550–558, 2016. 2, 4, 8