今天就来揭开多重背包的面纱！！！

Posted 2021-05-25 大忽悠爱忽悠

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了今天就来揭开多重背包的面纱！！！相关的知识，希望对你有一定的参考价值。

多重背包

题目描述
朴素二维
c++完整测试代码
滚动数组
一维空间优化
与其他背包的内在关系
总结

题目描述

有 N 种物品和一个容量为 C 的背包，每种物品「数量有限」。

第 i 件物品的体积是 v[i]，价值是 w[i]，数量为 s[i] 。

问选择哪些物品，每件物品选择多少件，可使得总价值最大。

其实就是在 0-1 背包问题的基础上，增加了每件物品可以选择「有限次数」的特点（在容量允许的情况下）。

示例 1：

输入: N = 2, C = 5, v = [1,2], w = [1,2], s = [2,1]   

输出: 4

解释: 选两件物品 1，再选一件物品 2，可使价值最大。

朴素二维

首先，几乎所有的「背包问题」都是基于「01 背包」演变而来。

因此，当我们确定一个问题是背包问题之后，可以根据其物品的「数量限制」来判别是何种背包问题，然后套用「01 背包」的思路来求解。

具体的，我们可以套用「01 背包」的「状态定义」来进行分析：

dp[i][j] 代表考虑前 i 件物品，且所选物品总体积不超过 j 时获得的最大价值。

由于每件物品可以被选择「有限次」，因此对于某个 dp[i][j] 而言，其值应该为以下所有可能方案中的最大值：

选择0件物品i的最大价值,即dp[i-1][j]
选择1件物品i的最大价值,即dp[i-1][j-v[i]]+w[i]
选择2件物品i的最大价值,即dp[i-1][j-2 * v[i]]+2 * w[i]
…
选择s[i] 件物品i的最大价值,即dp[i-1][j-s[i] * v[i]]+s[i] * w[i]

由此我们可以得出「状态转移方程」为：
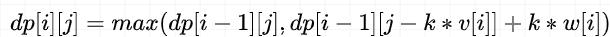
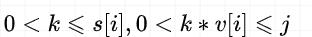
在这里插入图片描述

可以发现其状态转移方程与完全背包完全一致，只是多了 0<k<=s[i] 的条件。

也好理解，毕竟「完全背包」不限制物品数量，「多重背包」限制物品数量。

c++完整测试代码

多重背包题目测试链接

#include<iostream>
#include<vector>
using namespace std;
int s[100], v[100], w[100];//第i件物品最多有Si件，每件体积是Vi，价值是Wi
class Solution
{
public:
	int maxValue(int N, int V, int s[], int v[], int w[])
	{
		vector<vector<int>> dp(N, vector<int>(V + 1, 0));
		// 先处理第一件物品
		for (int i = 0; i <= V; i++)
		{
			// 显然当只有一件物品的时候，在容量允许的情况下，能选多少件就选多少件（不超过限制数量）
			int maxK = min(i / v[0], s[0]);
			dp[0][i] = maxK * w[0];
		}

		// 处理剩余物品
		for (int i = 1; i < N; i++)
		{
			for (int j = 0; j <=V; j++)
			{
				// 不考虑第 i 件物品的情况
				dp[i][j] = dp[i - 1][j];
				// 考虑第 i 件物品的情况
				for (int k = 1; k <= s[i]; k++)
				{
					//判断当前背包能否放下
					if (j < k * v[i]) break;
					dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k*w[i]);
				}
			}
		}
		return dp[N - 1][V];
	}
};
int main()
{
	int N, V;//N种物品，背包容量为V
	cin >> N >> V;
	for (int i = 0; i < N; i++)
		cin >> v[i] >> w[i] >> s[i];
	Solution sol;
	cout << sol.maxValue(N,V,s,v,w) << endl;
	return 0;
}

在这里插入图片描述

滚动数组

通过观察我们的「状态转移方程」可以发现，我们在更新某个 dp[i][x] 的时候只依赖于dp[i-1][y] 。

因此我们可以像 01 背包那样使用「滚动数组」的方式将空间优化到 O©。

代码：

#include<iostream>
#include<vector>
using namespace std;
int s[100], v[100], w[100];//第i件物品最多有Si件，每件体积是Vi，价值是Wi
class Solution
{
public:
	int maxValue(int N, int V, int s[], int v[], int w[])
	{
		vector<vector<int>> dp(2, vector<int>(V + 1, 0));
		// 先处理第一件物品
		for (int i = 0; i <= V; i++)
		{
			// 显然当只有一件物品的时候，在容量允许的情况下，能选多少件就选多少件（不超过限制数量）
			int maxK = min(i / v[0], s[0]);
			dp[0][i] = maxK * w[0];
		}

		// 处理剩余物品
		for (int i = 1; i < N; i++)
		{
			for (int j = 0; j <=V; j++)
			{
				// 不考虑第 i 件物品的情况
				dp[i&1][j] = dp[(i - 1)&1][j];
				// 考虑第 i 件物品的情况
				for (int k = 1; k <= s[i]; k++)
				{
					//判断当前背包能否放下
					if (j < k * v[i]) break;
					dp[i&1][j] = max(dp[i&1][j], dp[(i - 1)&1][j - k * v[i]] + k*w[i]);
				}
			}
		}
		return dp[(N - 1)&1][V];
	}
};
int main()
{
	int N, V;//N种物品，背包容量为V
	cin >> N >> V;
	for (int i = 0; i < N; i++)
		cin >> v[i] >> w[i] >> s[i];
	Solution sol;
	cout << sol.maxValue(N,V,s,v,w) << endl;
	return 0;
}

在这里插入图片描述

一维空间优化

在之前的「01 背包」和「完全背包」都可以进行「一维空间优化」。

其中「完全背包」的「一维空间优化」还能有效降低时间复杂度。

那么「多重背包」是否也能通过「一维空间优化」来降低时间复杂度呢？

答案是可以优化空间，但是不能降低时间复杂度。

因为当我们像「完全背包」那样只保留「容量维度」，并且「从小到大」遍历容量的话，我们在转移时是无法直接知道所依赖的到底使用了多少件物品的。

这个问题在「完全背包」里面无须关心，因为每件物品可以被选择无限次，而在「多重背包」则是不能忽略，否则可能会违背物品件数有限的条件。

因此，「多重背包」问题的「一维空间优化」并不能像「完全背包」那样使复杂度降低。

代码：

#include<iostream>
#include<vector>
using namespace std;
int s[100], v[100], w[100];//第i件物品最多有Si件，每件体积是Vi，价值是Wi
class Solution
{
public:
	int maxValue(int N, int V, int s[], int v[], int w[])
	{
		vector<int> dp(V + 1);

		for (int i = 0; i < N; i++)//物品
		{
			for (int j = V; j >= v[i];j--)//容量---从大到小---因为无法像完全背包那样每个物品都无限次放入
			{
				for (int k = 0; k <= s[i] && k * v[i] <= j; k++)//物品数量
				{
					dp[j] = max(dp[j], dp[j - k * v[i]] + k * w[i]);
				}
			}
		}
		return dp[V];
	}
};
int main()
{
	int N, V;//N种物品，背包容量为V
	cin >> N >> V;
	for (int i = 0; i < N; i++)
		cin >> v[i] >> w[i] >> s[i];
	Solution sol;
	cout << sol.maxValue(N,V,s,v,w) << endl;
	return 0;
}