leetcode 279. 完全平方数----完全背包的套路

Posted 2021-05-23 大忽悠爱忽悠

完全平方数题解集合

• 完全背包（朴素解法）
• 完全背包（进阶）
• BFS
• 记忆化递归

---

完全背包（朴素解法）

不了解完全背包问题的先看这篇文章

• 首先「完全平方数」有无限个，但我们要凑成的数字是给定的。
• 因此我们第一步可以将范围在 [1，n] 内的「完全平方数」预处理出来。
• 这一步其实就是把所有可能用到的数字先预处理出来。
• 同时由于题目没有限制我们相同的「完全平方数」只能使用一次。
• 因此我们的问题转换为：
• 给定了若干个数字，每个数字可以被使用无限次，求凑出目标值 n 所需要用到的是最少数字个数是多少。
• 这显然符合「完全背包」模型。
• 目前我们学过的两类背包问题（01 背包 & 完全背包）的原始状态定义都是两维：
• 第一维 i 代表物品编号
• 第二维 j 代表容量
• 其中第二维 j 又有「不超过容量 j 」和「容量恰好为 j」两种定义。
• 本题要我们求「恰好」凑出 n 所需要的最少个数。
• 因此我们可以调整我们的「状态定义」：
• dp[i][j] 为考虑前 i 个数字，凑出数字总和 j 所需要用到的最少数字数量

不失一般性的分析 dp[i][j] ，对于第 i个数字（假设数值为 t），我们有如下选择：

• 选 0 个数字 i ，此时有dp[i-1][j]
• 选 1 个数字 i，此时有 dp[i-1][j-t]+1
• 选 2 个数字 i，此时有 dp[i-1][j-2*t]+2
• …
• 选 k 个数字 i ，此时有dp[i-1][j-k*t]+k
• 因此我们的状态转移方程为：
  
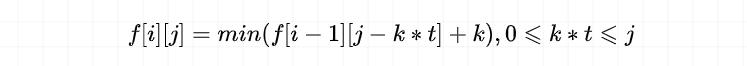
• 当然，能够选择 k 个数字 i 的前提是，剩余的数字 j-k*t 也能够被其他「完全平方数」凑出，即 dp[i-1][j - k * t] 为有意义的值。

代码：

class Solution {
public:
	int numSquares(int n) 
	{
	 //预处理出所有可能用到的「完全平方数」
	 //即算出所有物品的大小和物品的总数
		vector<int> v;
		int idx = 1;
		while (idx * idx <= n)
		{
			v.emplace_back(idx * idx);
			idx++;
		}
		int num = v.size();//物品的个数

	  //dp[i][j] 代表考虑前 i 个物品，凑出 j 所使用到的最小元素个数
		vector <vector<int>> dp(num,vector<int>(n+1,0));

		//处理第一个物品的所有情况
		int s1 = v[0];//获取第一个物品的大小
		for (int i = 0; i <= n; i++)
		{
			//计算当前容量下最多能塞入当前物品个数
			int k = i / s1;
			//这里处理的刚好塞满的版本，因此只有背包刚好塞满才算可行方案
			if (k * s1 == i)// 只有容量为第一个数的整数倍的才能凑出
				dp[0][i] = k;//这里的k也同样是当前塞入物品的个数
			else
				dp[0][i]=INT_MIN;// 其余则为无效值
		}

		//处理剩余数的情况
		for (int i = 1; i < num; i++)
		{
			int s = v[i];//获取第i个物品的大小
			for (int j = 0; j <= n; j++)
			{
				// 对于不选第 i 个物品的情况
				dp[i][j] = dp[i - 1][j];

				//选第i个物品的情况，还要看第i个物品选了几个
				for (int k = 1; k * s <= j; k++)
				{
					// 能够选择 k 个 t 的前提是剩余的数字 j - k * t 也能被凑出
					if(dp[i-1][j-k*s]!= INT_MIN)
						dp[i][j] = min(dp[i][j], dp[i - 1][j - k * s] + k);
				}
			}
		}
		return dp[num - 1][n];
	}
};

---

完全背包（进阶）

显然朴素版的完全背包进行求解复杂度有点高。

在完全背包道题目讲解 的时候，我们从「数学」角度来推导为何能够进行一维空间优化。

这次我们还是按照同样的思路再进行一次推导，加强大家对这种优化方式的理解。

从二维的状态转移方程入手进行分析（假设第 i 个数字为 t）：

至此，我们得到了最终的状态转移方程：

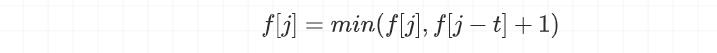
代码:

class Solution {
public:
	int numSquares(int n) 
	{
	 //预处理出所有可能用到的「完全平方数」
	 //即算出所有物品的大小和物品的总数
		vector<int> v;
		int idx = 1;
		while (idx * idx <= n)
		{
			v.emplace_back(idx * idx);
			idx++;
		}
		int num = v.size();//物品的个数

	   // dp[j] 代表考虑到当前物品为止，凑出 j 所使用到的最小元素个数
		vector <int> dp(n+1);

		//处理第一个物品的所有情况
		int s1 = v[0];//获取第一个物品的大小
		for (int i = 0; i <= n; i++)
		{
			//计算当前容量下最多能塞入当前物品个数
			int k = i / s1;
			//这里处理的刚好塞满的版本，因此只有背包刚好塞满才算可行方案
			if (k * s1 == i)// 只有容量为第一个数的整数倍的才能凑出
				dp[i] = k;//这里的k也同样是当前塞入物品的个数
			else
				dp[i] = INT_MIN;// 其余则为无效值
		}

		//处理剩余数的情况
		for (int i = 1; i < num; i++)
		{
			int s = v[i];//获取第i个物品的大小
			for (int j = s; j <= n; j++)//当前背包容量至少能放下当前物品，因此从s开始
			//放不下那就跳过当前容量，维持原本的数据
			{
				// 当不更新 dp[j] 的时候，对应了二维表示中的 dp[i - 1][j],即dp[j]=dp[j]

			   // 可以更新 dp[j] 的前提是：剩余的 j - k * t 也能够被凑出
			   // 更新 dp[j] 所依赖的 dp[j - s] 对应了二维表示中的 dp[i - 1][j - k * s]
					if(dp[j-s]!= INT_MIN)
						dp[j] = min(dp[j], dp[j -s]+1);
			}
		}
		return dp[n];
	}
};

---

BFS

• 这题让求的是若干个平方数的和等于n，并且平方数的个数最少。首先我们可以把它想象成为一颗m叉树，树的每一个节点的值都是平方数的和，如下图所示。
• 每一个节点的值都是从根节点到当前节点的累加。而平方数的个数其实就是遍历到第几层的时候累加和等于target。我们只需要一层一层的遍历，也就是常说的BFS，当遇到累加的和等于target的时候直接返回当前的层数即可。

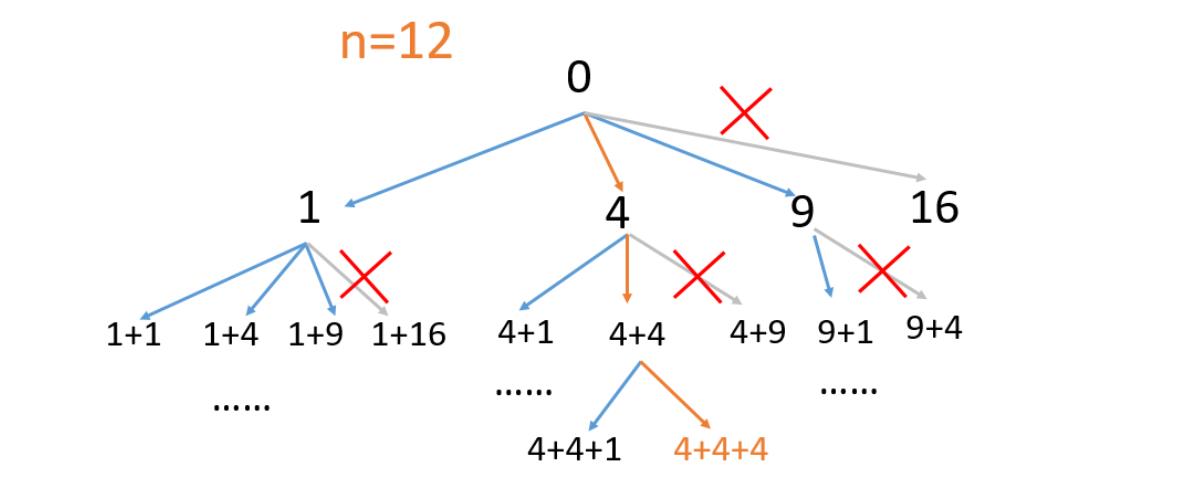
• 二叉树的BFS遍历像下面这样
  
• 他的伪代码很简单

void levelOrder(TreeNode* tree) {
    queue<TreeNode*> queue ;
    queue.add(tree);
    int level = 0;//统计有多少层
    while (!queue.isEmpty()) {
        //每一层的节点数
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            //打印节点
            System.out.println(node.val);
            if (node.left != null)
                queue.add(node.left);
            if (node.right != null)
                queue.add(node.right);
        }
        level++;
        //打印第几层
        System.out.println(level);
    }
}

• 我们只需要对他稍作修改就是今天这题的答案了，但是还有一点，就是防止重复计算
• 看下图：
  

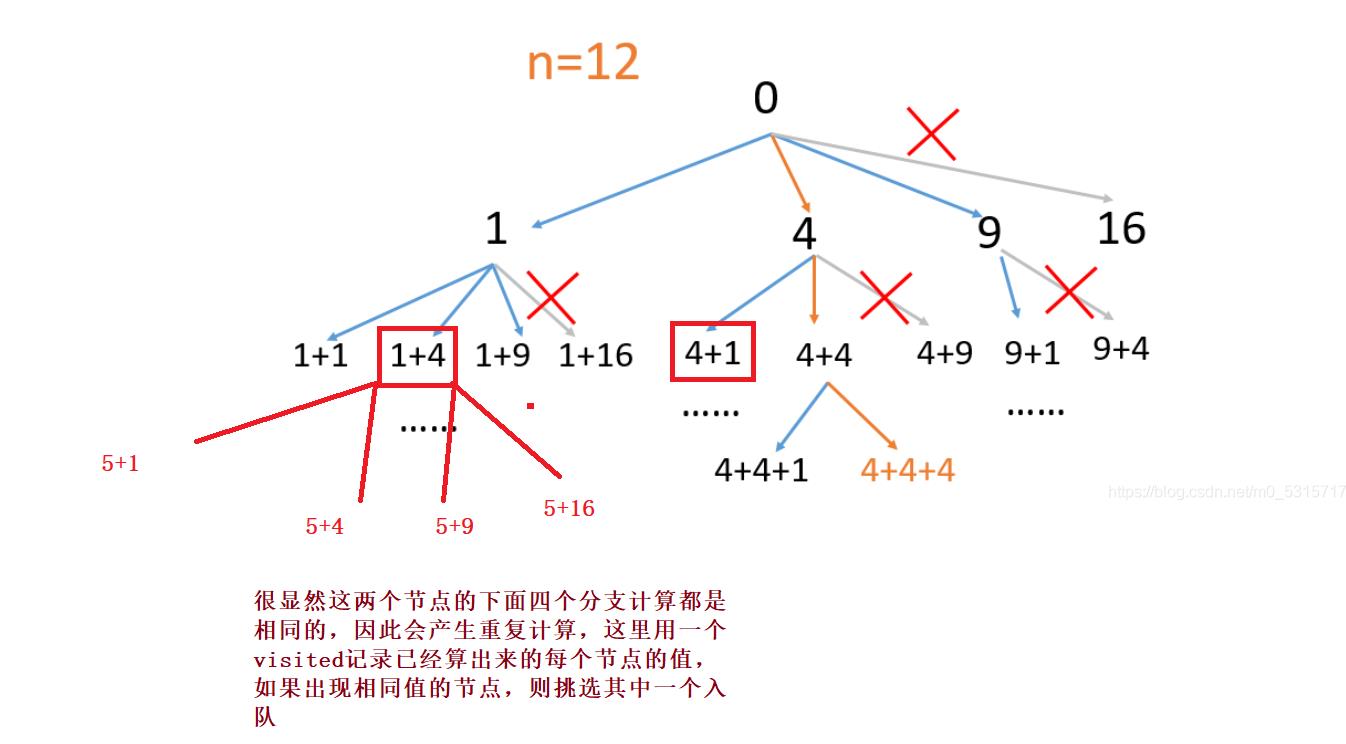
代码：

class Solution {
public:
	int numSquares(int n) 
	{
		queue<int> q;
		//记录已经访问的节点值
		unordered_set<int> set;
		//根节点值为0，即初始累加值为0
		q.push(0);
		set.insert(0);
		//记录当前层数--当前已经使用了几个数字
		int level = 0;
		while (!q.empty())
		{
			//当前层节点数量
			int size = q.size();
			//层数加1
			level++;
			//遍历当前层的节点
			for (int i = 0; i < size; i++)
			{
				//获取当前节点的值
				int curVal = q.front();
				q.pop();
				//访问当前节点的子节点
				for (int j = 1; j <= n; j++)
				{
					//子节点的值
					int nodeValue = curVal + j * j;
					//nodeValue始终是完全平方数的和，当他等于n的
					//时候直接返回
					if (nodeValue == n)
						return level;
					//如果大于n，终止内层循环
					if (nodeValue > n)
						break;
					//判断当前子节点的值是否出现过
					if (set.find(nodeValue) == set.end())
					{
						//入队
						q.push(nodeValue);
						//设置当前节点为访问过
						set.insert(nodeValue);
					}
				}
			}
		}
		return level;
	}
};

---

记忆化递归

思路：

• 按照BFS的方法，把问题转化为多叉树遍历的问题，就很简单了，这里用map容器保留计算结果，防止重复计算

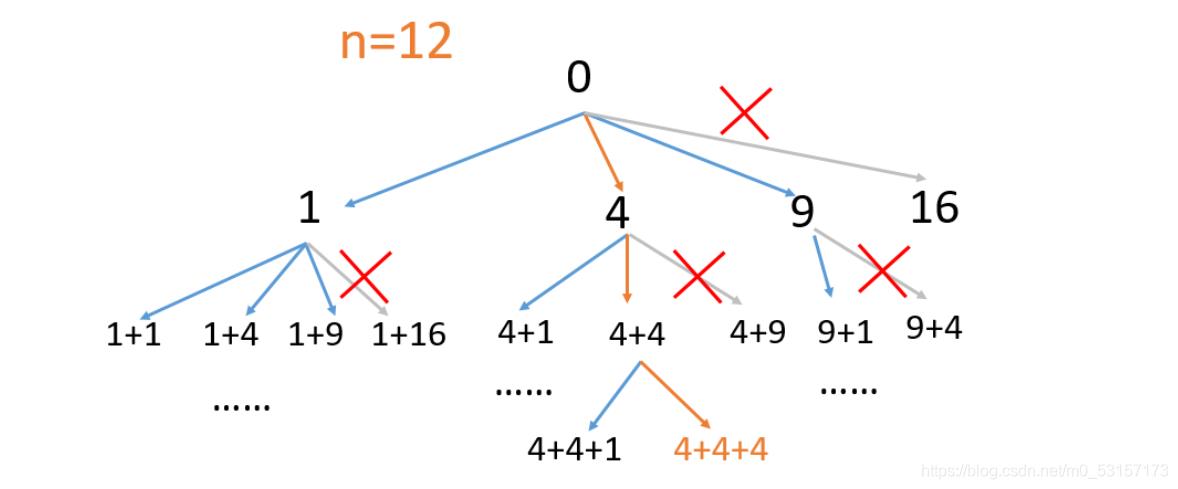
递归三部曲:

• 结束条件:当前累加值等于目标值或者当前累加值大于目标值
• 返回值:返回当前累加和需要使用的最少数字个数
• 本级递归做什么:计算当前累加和需要的最少数字

代码:

class Solution {
	map<int, int> cache;//缓存器
public:
	int numSquares(int n) 
	{
		if (cache.find(n) != cache.end()) return cache[n];
		if (n == 0) return 0; //递归符合，中止条件
		if (n < 0) return INT_MAX;//递归出界 
		int ans = INT_MAX;
		for (int j = 1; j * j <= n; j++)
           ans=min(ans,numSquares(n - j * j)+1);
		return cache[n]=ans;
	}
};

• 这里使用了map容器记忆化递归会超时，需要改用unordered_map容器
• 因为两者底层实现方法不同，一个是红黑树，一个是哈希表
• 相对来说后者查找速度更快

class Solution {
	unordered_map<int, int> cache;//缓存器
public:
	int numSquares(int n)
	{
		if (cache.find(n) != cache.end()) return cache[n];
		if (n == 0) return 0; //递归符合，中止条件
		if (n < 0) return INT_MAX;//递归出界 
		int ans = INT_MAX;
		for (int j = 1; j * j <= n; j++)
			ans = min(ans, numSquares(n - j * j) + 1);
		return cache[n] = ans;
	}
};