LintCode 125 · 背包问题---01背包问题

Posted 2021-05-20 大忽悠爱忽悠

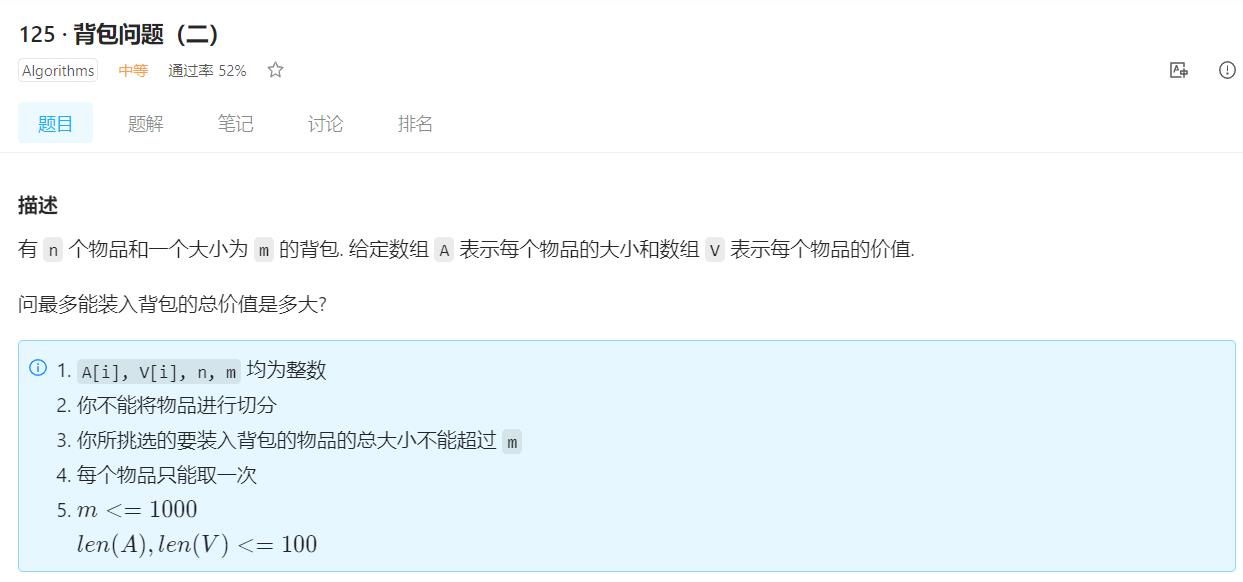
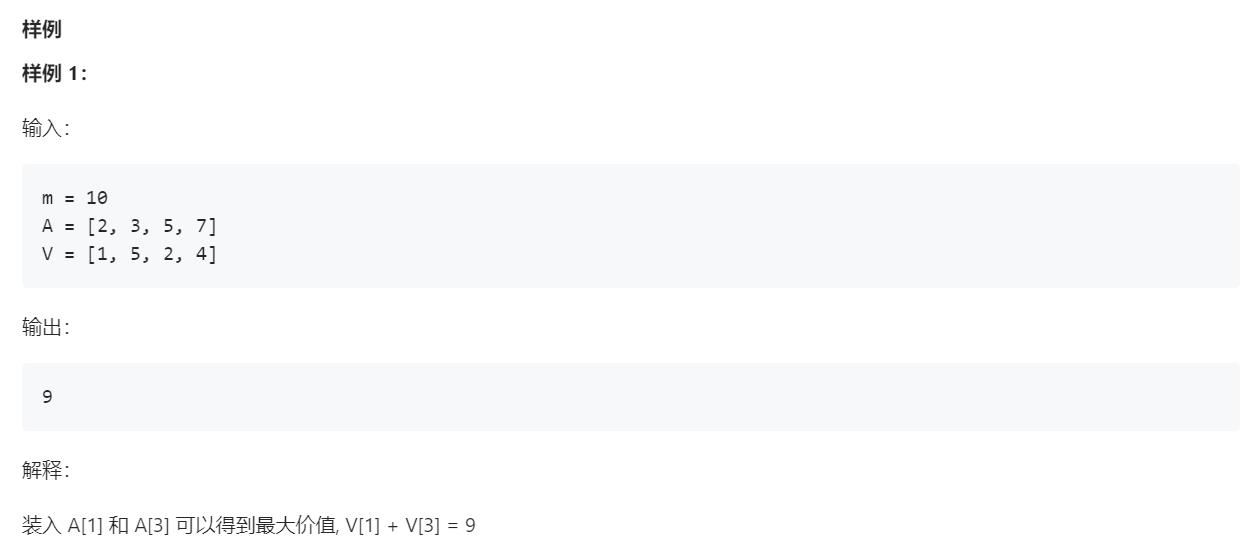
背包问题（二）题解集合

• 记忆化搜索
• 动态规划
• 滚动数组优化--dp[2][C+1] 解法
• dp[C+1] 解法
• 总结

---

记忆化搜索

• 如果要我们设计一个 DFS 函数对所有的方案进行枚举的话，大概是这么一个函数签名：

int dfs (int[] v, int[] w, int i, int c);

• 其中 v 和 w 对应了输入的「物品体积」和「物品价值」，属于不变参数，无须考虑。
• 而 i 和 c 分别代表「当前枚举到哪件物品」和「现在的剩余容量」。
• 返回值则是我们问题的答案：最大价值。
• 当然我们还需要一个缓存器cache，来保存已经计算出的结果

递归三部曲:

• 结束条件:当枚举到第一件物品时
• 返回值:返回当前物品对应剩余容量的最大价值
• 本级递归做什么:计算当前物品对应剩余容量状态下的最大价值

代码:

class Solution {
	map<pair<int,int>,int> cache;//缓存器---第i个物品对应j容量下，最大价值val
public:
	int backPackII(int m, vector<int>& A, vector<int>& V) 
	{
		return dfs(A.size() - 1, m, A, V);
	}
	//当前物品，对应容量，物品大小数组，物品价值数组
	int dfs(int index,int cap, vector<int>& Size, vector<int>& Val)
	{
		if (index == 0)//只有一个物品可选择时，当前背包对应的最大价值就是第一个物品的价值---前提是能放的下
		{
			return cap >= Size[0] ? Val[0] : 0;//当枚举到第一个物品时，要判断当前背包容量能否放的下第一个物品
		}
		//已经计算出结果，直接返回
		if (cache.find({ index,cap }) != cache.end()) return cache[{index, cap}];
		//下面计算当前对应第i个物品背包容量为j下，求解背包最大价值
		//选
		int sel = 0;
		//看能不能放的下---如果放不下就是没选
		if (cap >= Size[index])
		{
			sel = dfs(index - 1, cap - Size[index], Size, Val)+Val[index];
		}
		//不选
		int unsel = dfs(index - 1, cap, Size, Val);

		//当前最大值两者取其大
		return cache[{index, cap}] = max(sel, unsel);
	}
};

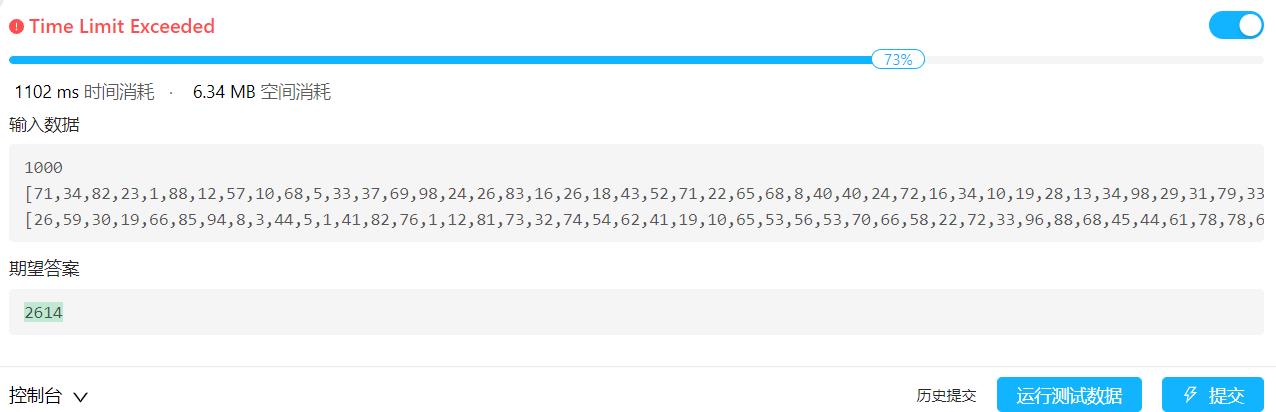
但是这里记忆化递归也会超时

---

动态规划

• 如果要我们设计一个 DFS 函数对所有的方案进行枚举的话，大概是这么一个函数签名：

int dfs (int[] v, int[] w, int i, int c);

• 其中 v 和 w 对应了输入的「物品体积」和「物品价值」，属于不变参数，无须考虑。
• 而 i 和 c 分别代表「当前枚举到哪件物品」和「现在的剩余容量」。
• 返回值则是我们问题的答案：最大价值。

那么根据变化参数和返回值，可以抽象出我们的 dp 数组：
一个二维数组，其中一维代表当前「当前枚举到哪件物品」，另外一维「现在的剩余容量」，数组装的是「最大价值」。

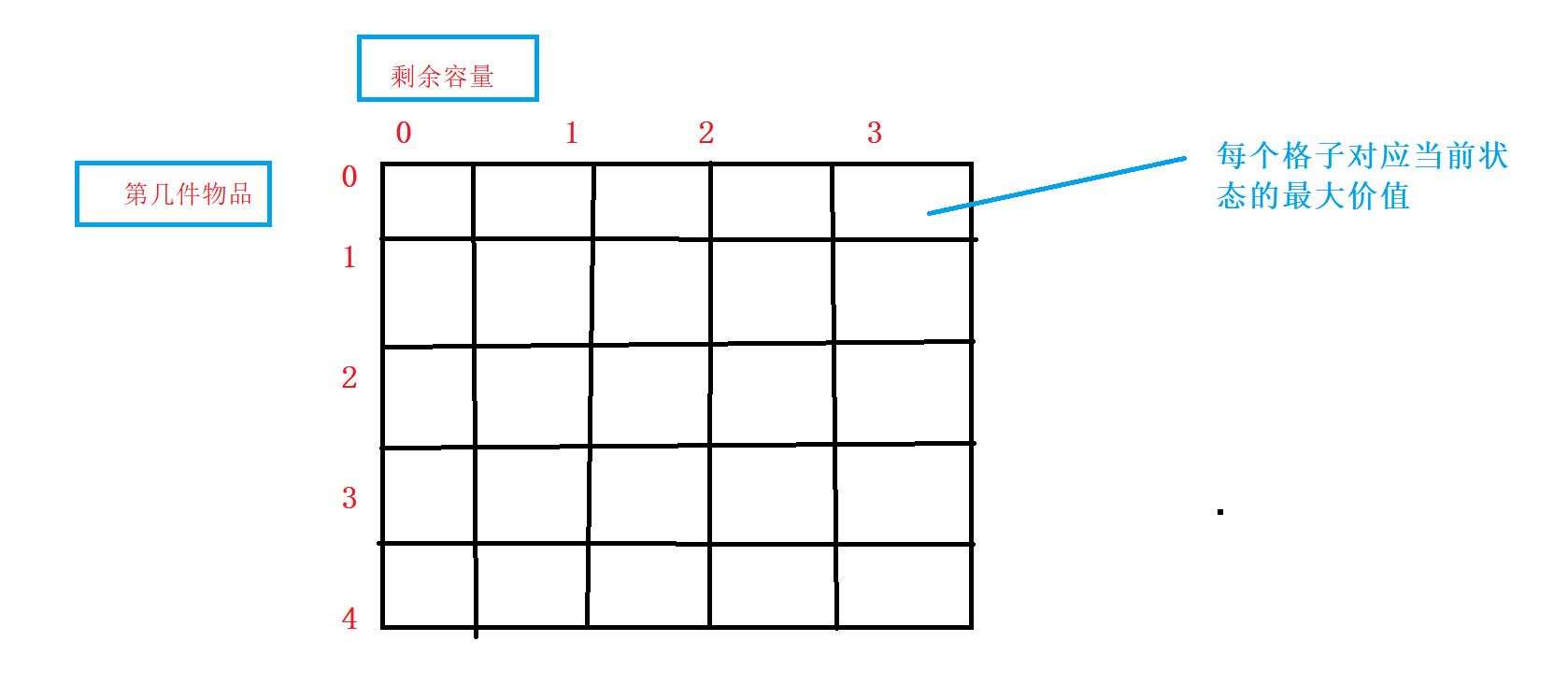
根据 dp 数组不难得出状态定义：

考虑前 i 件物品，使用容量不超过 C 的条件下的背包最大价值。

结合我们的「状态定义」，「不选」方案的「最大价值」很好确定：

「不选」其实就是dp[i-1][c] ，等效于我们只考虑前 i-1 件物品，当前容量为 c 的情况下的最大价值。

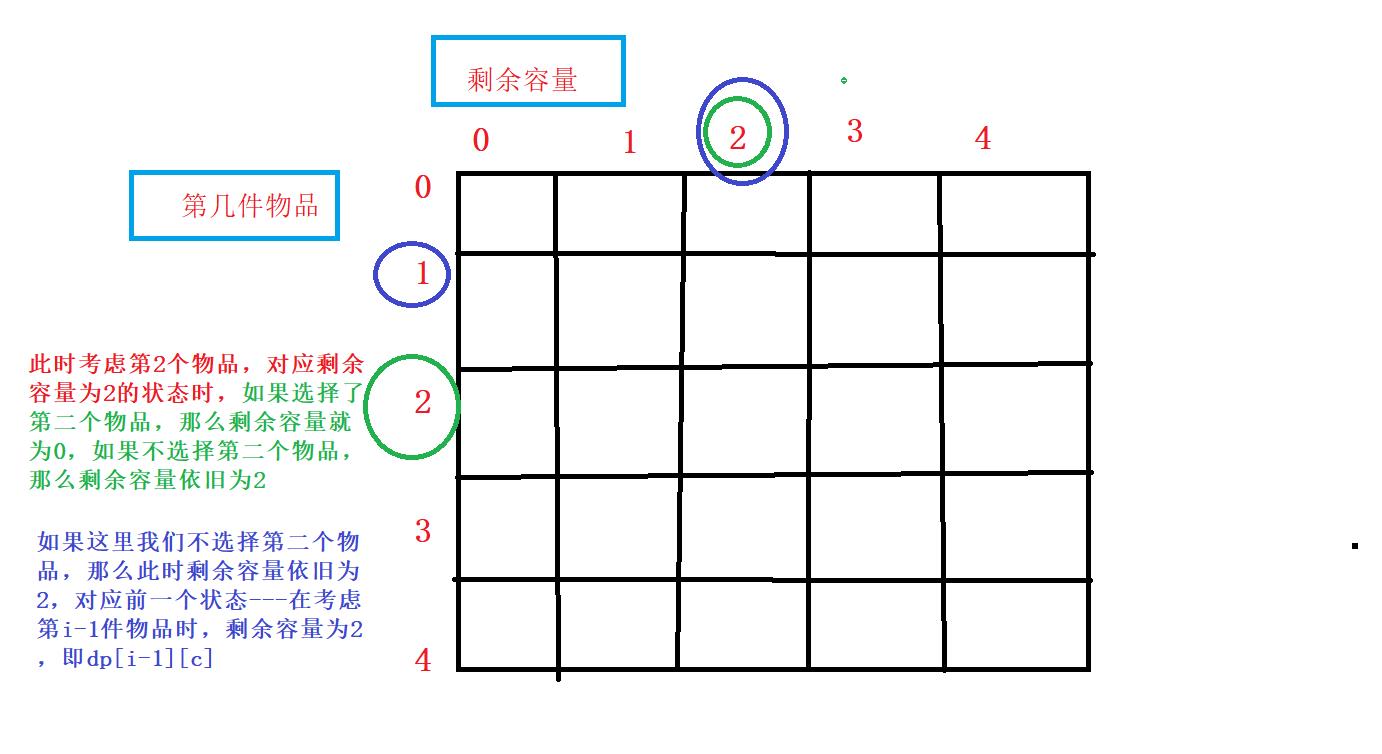
• 其实类似于一个层层前推的过程，如果第i-1个物品也不选，那么就考虑第i件物品，对应剩余容量为2时的状态
• 注意：这里每个格子对应的含义是枚举到当前物品时，背包剩余容量大小
• 同理，如果我们选第 i 件物品的话，代表消耗了v[i] 的背包容量，获取了w[i] 的价值，那么留给前 i-1件物品的背包容量就只剩c-v[i] 。即最大价值为dp[i-1][c-v[i]]+w[i]
  
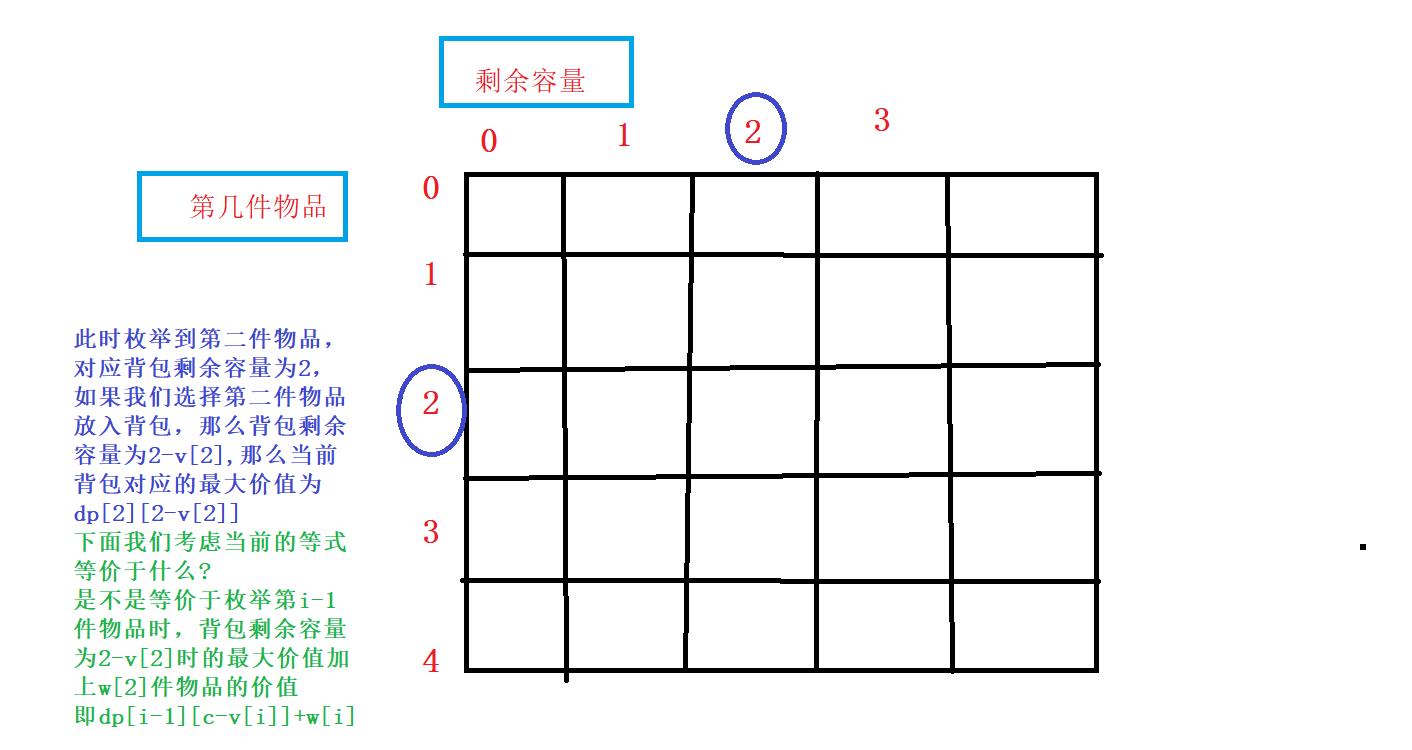
• 当然，选第 i 件有一个前提：「当前剩余的背包容量」>=「物品的体积」。
• 在「选」和「不选」之间取最大值，就是我们 i「考虑前 i 件物品，使用容量不超过 c」的条件下的「背包最大价值」。
• 即可得「状态转移方程」为：
  

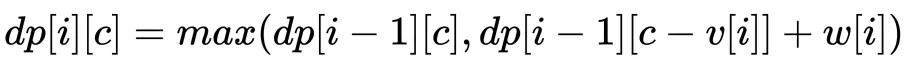
代码:

class Solution {
public:
	int backPackII(int m, vector<int>& A, vector<int>& V) 
	{
		int n = A.size();//n个物品
		vector<vector<int>> dp(n, vector<int>(m + 1, 0));//因为需要考虑容量从[0,m]闭区间范围，因此这里是m+1
		//最小子问题---第一件物品选与不选的状态对应的值
		//即初始化二维数组的第一行
		//当只有一件物品可选时，要求当前背包最大价值，当然是能往背包放就往背包里面放啦
		for (int i = 0; i <= m; i++)
		{
			dp[0][i] = i >=A[0] ? V[0] : 0;//枚举到当前背包容量如果可以放下第一个物品，那么最大价值等于第一个物品的价值
		}

		//有了第一件物品的所有状态，我们就可以根据第一件物品的所有状态求解出第二件物品的所有状态....第三件，第四件....第n件
		//即有了二维数组第一行所有值后，就可以挨个求出第二行所有值,,,,第n行
		for (int i = 1; i < n; i++)//枚举每一个物品
		{
			for (int j = 0; j <= m; j++)//计算列----从0到m依次计算当前物品对应每一个背包容量的状态下的最大价值
			{
				//不选当前物品
				int sel = dp[i - 1][j];
				//选择当前物品----前提是背包剩余容量能够放下这件物品
				int  unsel = j>=A[i]?dp[i - 1][j - A[i]] + V[i]:0;

				//当前状态下的最大价值是从选与不选中挑选最大者
				dp[i][j] = max(sel, unsel);
			}
		}
		//最后返回第n件物品，对应容量为C状态下的最大价值
		return dp[n - 1][m];
	}
};

---

滚动数组优化–dp[2][C+1] 解法

• 根据「转移方程」，我们知道计算第 i 行格子只需要第 i -1 行中的某些值。
• 也就是计算「某一行」的时候只需要依赖「前一行」。
• 因此可以用一个只有两行的数组来存储中间结果，根据当前计算的行号是偶数还是奇数来交替使用第 0 行和第 1 行。
• 这样的空间优化方法称为「滚动数组」
• 这种空间优化方法十分推荐，因为改动起来没有任何思维难度。
• 只需要将代表行的维度修改成 2，并将所有使用行维度的地方从 i 改成 i% 2或者 i&1 即（更建议使用 i&1 ，i & 1运算在不同 CPU 架构的机器上要比 % 运算稳定）。

代码：

class Solution {
public:
	int backPackII(int m, vector<int>& A, vector<int>& V) 
	{
		int n = A.size();
		vector<vector<int>> dp(2, vector<int>(m + 1, 0));
		for (int i = 0; i <= m; i++)
			dp[0][i] = i >= A[0] ? V[0] : 0;
		for (int i = 1; i < n; i++)
		{
			for (int j = 0; j <= m; j++)
			{
				int sel = dp[(i - 1)&1][j];
				int  unsel = j>=A[i]?dp[(i - 1)&1][j - A[i]] + V[i]:0;
				dp[i&1][j] = max(sel, unsel);
			}
		}
		return dp[(n - 1)&1][m];
	}
};

---

dp[C+1] 解法

• 事实上，我们还能继续进行空间优化，只保留代表「剩余容量」的维度。
• 再次观察我们的「转移方程」：
  
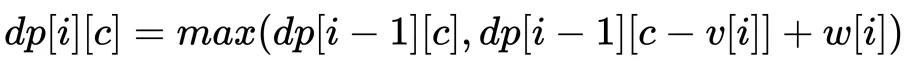
• 不难发现当求解第 i 行格子的值时，不仅是只依赖第 i-1 行，还明确只依赖第 i-1 行的第 C个格子和第 C-V[i]个格子（也就是对应着第 i 个物品不选和选的两种情况）。
• 换句话说，只依赖于「上一个格子的位置」以及「上一个格子的左边位置」。
  
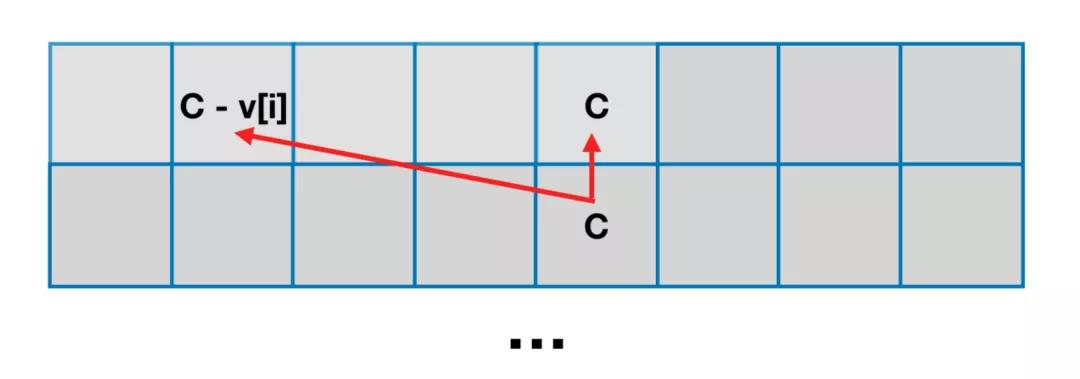
• 因此，只要我们将求解第 i 行格子的顺序「从 0 到 c 」改为「从 c 到 0」，就可以将原本 2 行的二维数组压缩到一行（转换为一维数组）。
• 这样做的空间复杂度和「滚动数组」优化的空间复杂度是一样的。但仍然具有意义，而且这样的「一维空间」优化，是求解其他背包问题的基础，需要重点掌握。

代码：

class Solution {
public:
	int backPackII(int m, vector<int>& A, vector<int>& V) 
	{
		vector<int> dp(m + 1);//当前数组的列表示容量的维度
		int n = A.size();//物品的个数
		for (int i = 0; i < n; i++)//还是是滚动行数组的概念，从第一行开始计算，
	//计算第二行时，因为会用到第一行前面的数据，因此从第一行尾端往前端进行覆盖
		{
			for (int j = m; j >= A[i]; j--)//计算列，当前背包容量必须大于需要放进去的物品，不然放不进去，也就不需要进行计算了
			{
				//不选当前物品
				int sel = dp[j];
				//选当前物品
				int unsel = dp[j - A[i]]+V[i];

				dp[j] = max(sel, unsel);
			}
		}
		return dp[m];
	}
};

---

总结

以上就是今天对经典0-1背包问题的一个小小总结，后续还会更新其他背包问题，欢迎大家持续关注