c语言-猴子选大王-约瑟夫问题（队列，链表，数组）

Posted 2021-05-20 joker D888

猴子选大王

• 前言：初读此题，根据题意，顺势想到了用刚学的数据结构中的循环队列及循环链表，便想借此来熟练一下新学知识。

• 题目描述：
  一群猴子要选新猴王。新猴王的选择方法是：让N只候选猴子围成一圈，从某位置起顺序编号为1~N号。从第1号开始报数，每轮从1报到3，凡报到3的猴子即退出圈子，接着又从紧邻的下一只猴子开始同样的报数。如此不断循环，最后剩下的一只猴子就选为猴王。请问是原来第几号猴子当选猴王？

• 解题思路：循环队列，循环链表，数组三种解题思路。

• 循环队列法

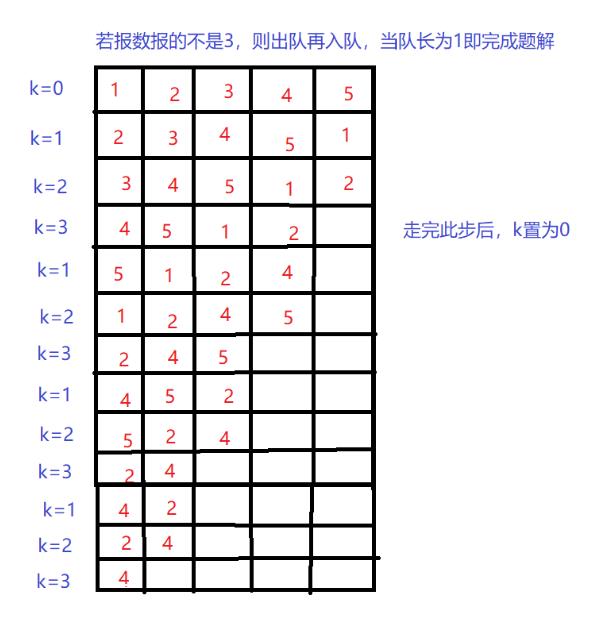
• 思路：借助队列的概念，前出后进，若报数的猴子不是3，则先出队再入队，若是3，直接出队。借助变量k来记录猴子所报的数，开始置为0，每一次循环k++，若k=3,删除对头（即出队）再将k置为0。以下图解配和代码食用更加美味。（此处以n=7为例）
  

#include<stdio.h>
typedef struct Queue
{
	int* base;//初始化的动态分配储存空间
	int rear;//对尾，指向队尾元素的下一个位置
	int front;//对头，指向队列头元素
}Queue;
void EnQueue(Queue* Q,int x)
{
	//因为此题队列元素只会少不会多，在此就不判读队满
	Q->base[Q->rear] = x;
	Q->rear = (Q->rear + 1) % n;

}
int DeQueue(Queue* Q)
{
	int e = Q->base[Q->front];
	Q->front = (Q->front + 1) % n;
	return e;
}
int QueueLength(Queue* Q)
{
	return (Q->rear - Q->front + n) % n;
}
int Monkey1()
{
	Queue Q;
	Q.base = (int*)malloc(n * sizeof(int));
	Q.front = Q.rear = 0;
	for (int i = 1; i < n; i++)
	{
		EnQueue(&Q, i);
	}
	int k = 0;

	while (QueueLength(&Q) > 1)
	{
		k++;
		if (k == 3)
		{
			DeQueue(&Q);
			k = 0;
		}
		else
		{
			EnQueue(&Q, DeQueue(&Q));
		}
	}

	return Q.base[Q.front];
}
int n;//全局变量
int main(void)
{
	scanf("%d", &n);
	n++;//因此循环队列要留一空元素空间进行判断是否队列满，所以++,以便后续开辟空间和Q.front和Q.rear的循环移动
	int ret=Monkey1();
	printf("%d\\n", ret);
	return 0;
}

• 循环链表法(最易理解，最符合题目需求）
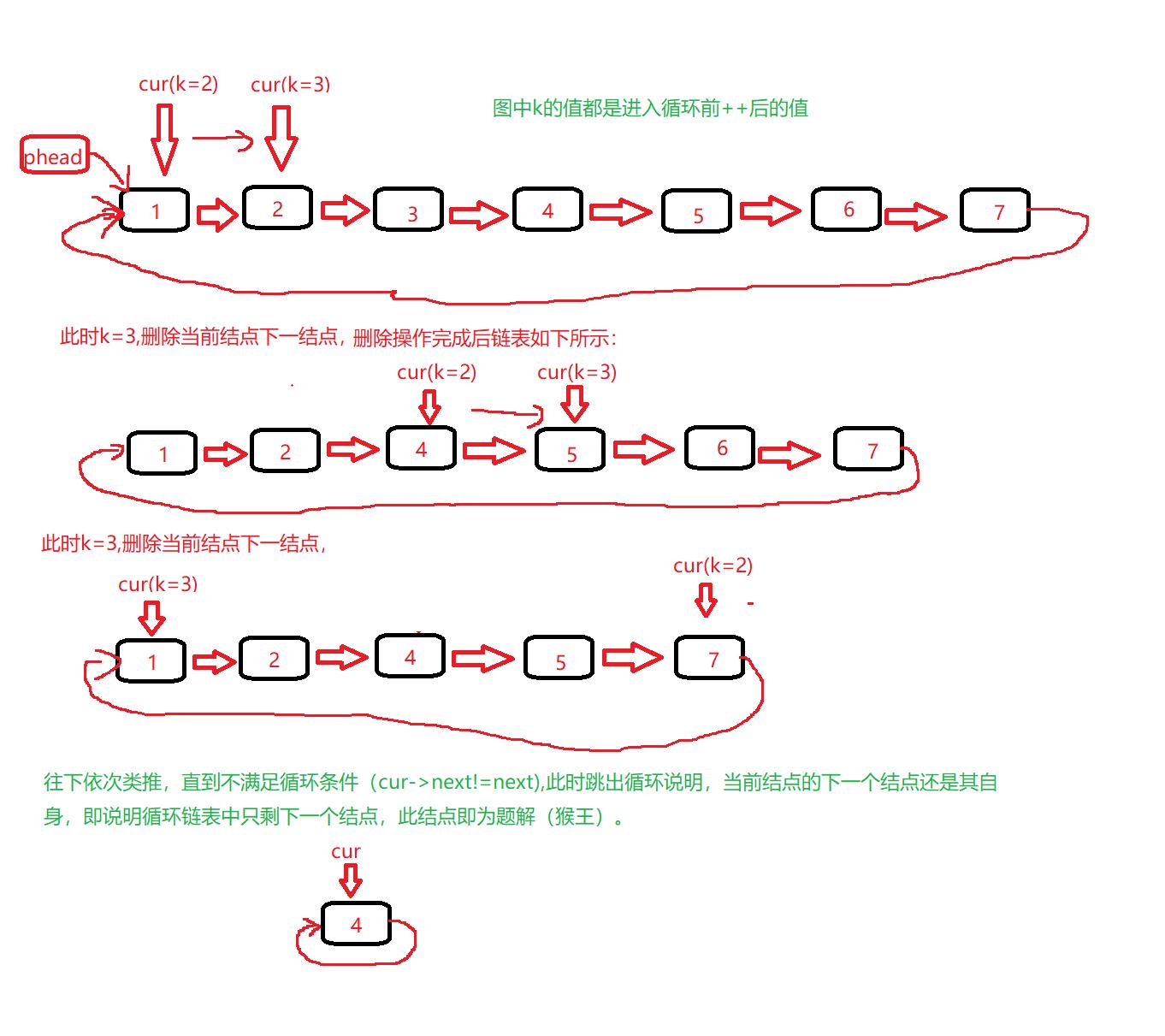
  思路：借助循环链表可以高效实现环中结点的删除。因单向链表可以较为简便的删除某结点之后的结点，不易实现删除当前结点（也可以使用双向链表），所以在此将k初始化为1，以实现删除报数为3的结点。与上面的思路类似，当k=3时，删除当前结点的下一结点，再将k置为1，往下依次类推。图解请配合代码一起食用。
  

#include<stdio.h>
int n;//全局变量
typedef struct ListNode
{
	int data;
	struct ListNode* next;
}LNode;
LNode* BuyLNode(int x)
{
	LNode* new = (LNode*)malloc(sizeof(LNode));
	new->next = NULL;
	new->data = x;
	return new;
}

int Monkey2()
{
	int i = 0;

	LNode* phead = BuyLNode(i);
	LNode* cur = phead;
	for (i = 1; i <= n; i++)
	{
		cur->next = BuyLNode(i);
		cur = cur->next;
	}
	cur->next= phead->next;//最后链接到头上

	cur = phead->next;
	int k =1;//因此链表为单向链表，只能删除下一个结点，所以在此将k置为1；
	while (cur->next != cur)
	{
		k++;
		if (k == 3)
		{
			//删除下一个结点
			LNode* next = cur->next->next;
			free(cur->next);
			cur->next = next;

			cur = cur->next;
			k = 1;
		}
		else
		{
			cur = cur->next;
		}
	}
	return cur->data;
}
int main(void)
{
	scanf("%d", &n);
	int ret = Monkey2();
	printf("%d\\n", ret);
	return 0;
}

• 普通方法（数组法，实现简单）
  思路：创建一个n+1（自己输入）个空间大小整型数组，将数从1到赋值到n给猴子编号，设置两个变量，一个变量k记录报数，另一个变量count记录猴子个数，k初始为0，还是当k=3时，删除当前元素（猴子），即将当前元素置为0，再将k置为0，依次类推。当count=1时跳出循环，完成题解。

#include<stdio.h>
int n;
int Monkey3()
{
	int* arr = (int*)malloc((n+1)*sizeof(int));
	int i;
	for (i = 1; i <= n; i++)
	{
		arr[i] = i;
	}
	int k = 0;
	int count = n;
	while (count > 1)//不断的遍历数组，直到猴子数为1
	{
		for (i = 1; i <= n; i++)
		{
			if (arr[i] == 0)
			{
				//当arr[i]=0,即说明此编号为i的猴子已被淘汰，直接i++跳到下一个猴子
				continue;
			}
			k++;
			
			if (k == 3)
			{
				arr[i] = 0;
				count--;//猴子数减一
				k = 0;
			}
		}
	}
	for (i = 1; i <= n; i++)
	{
		//找出不为0的元素，即为猴王
		if (arr[i] != 0)
			return arr[i];
	}

}
int main(void)
{
	scanf("%d", &n);
	int ret = Monkey3();
	printf("%d\\n", ret);
	return 0;
}

如有错误欢迎指出，或提出你的解题思路或看法。