leetcode 124. 二叉树中的最大路径和

Posted 2021-05-16 大忽悠爱忽悠

1.递归法思路：

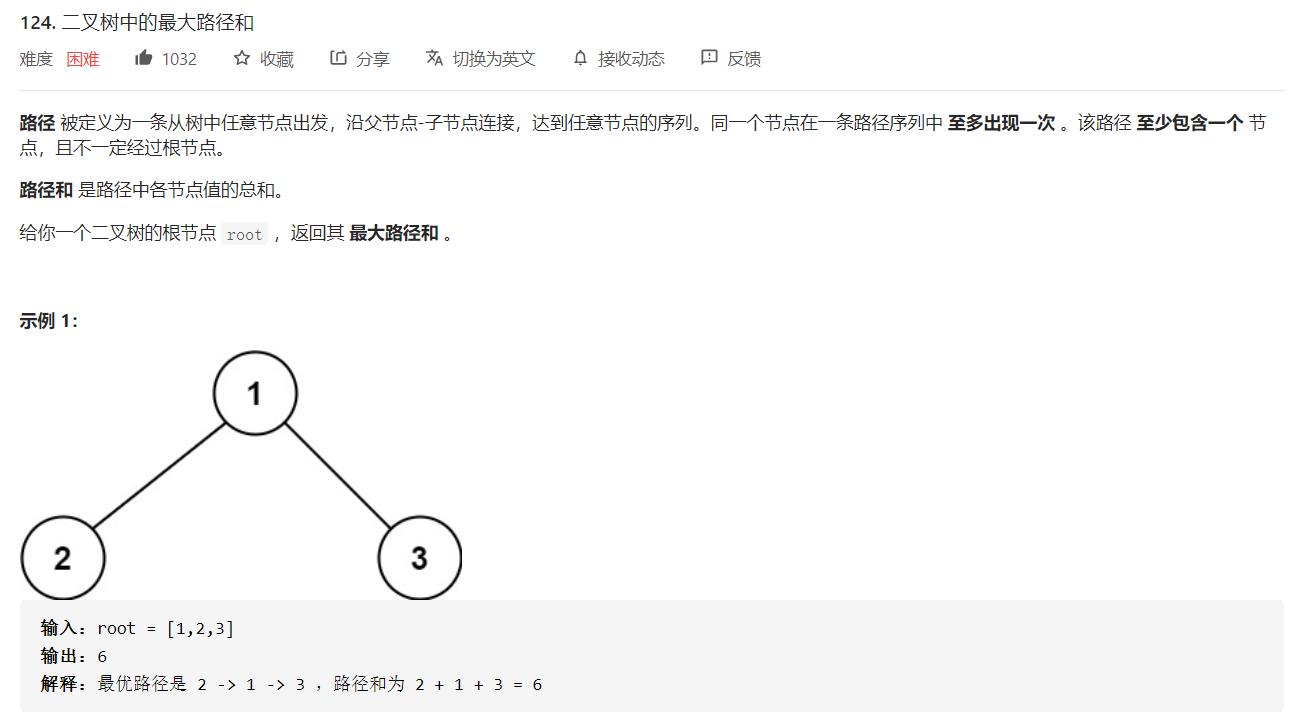
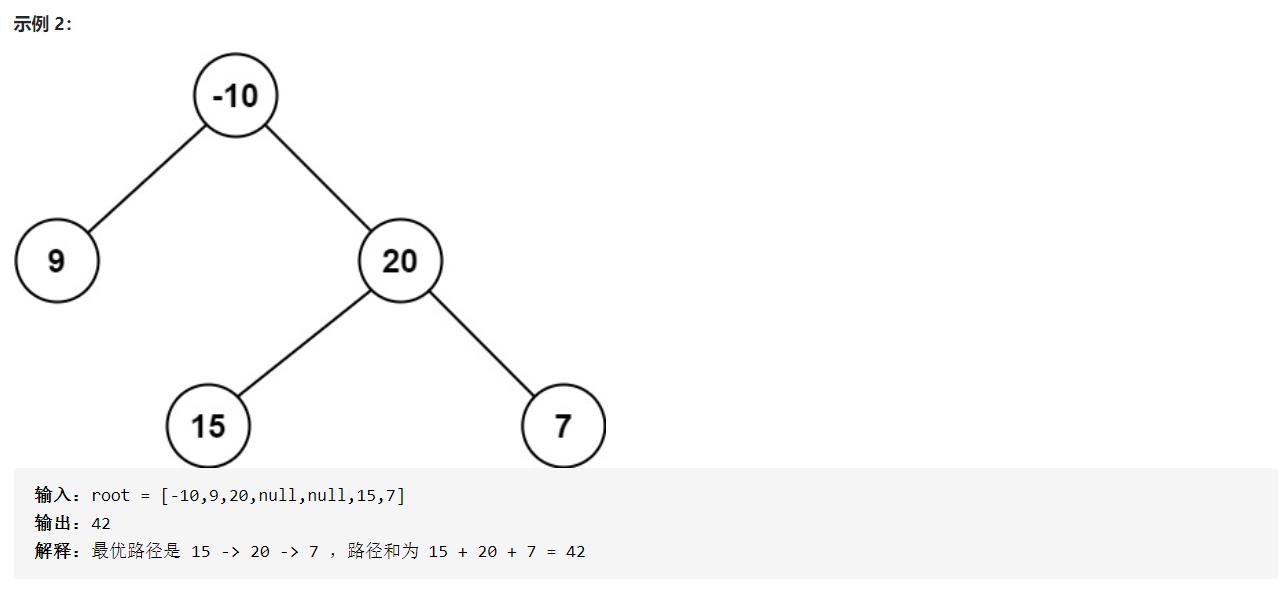
• 题目要求最大路径和，对于一个二叉树节点，是不是先计算左子树和右子树的最大路径和，然后加上自己的值，这样就得出新的最大路径和了？所以说这里其实可以套后序遍历模板框架。

class Solution {
public:
    int ans = INT_MIN;//用来更新当前二叉的最大路径和
	int maxPathSum(Treenode* root) 
    {
        sideMax(root);
        return ans;
	}
    int sideMax(Treenode* root)
    {
        if (root == NULL) return 0;
         //计算左边分支最大值，左边分支如果为负数还不如不选择
        int left = max(0, sideMax(root->left));
        //计算右边分支最大值，右边分支如果为负数还不如不选择
        int right = max(0, sideMax(root->right));
        //看是否需要更新当前二叉树的最大路径和
        ans = max(ans, left + right + root->val);
        //最大路径和等于:左右子树中的最大路径和加上自身的值
        return max(left, right) + root->val;
    }
};

递归法的详细解释：
笨猪爆破组原文链接

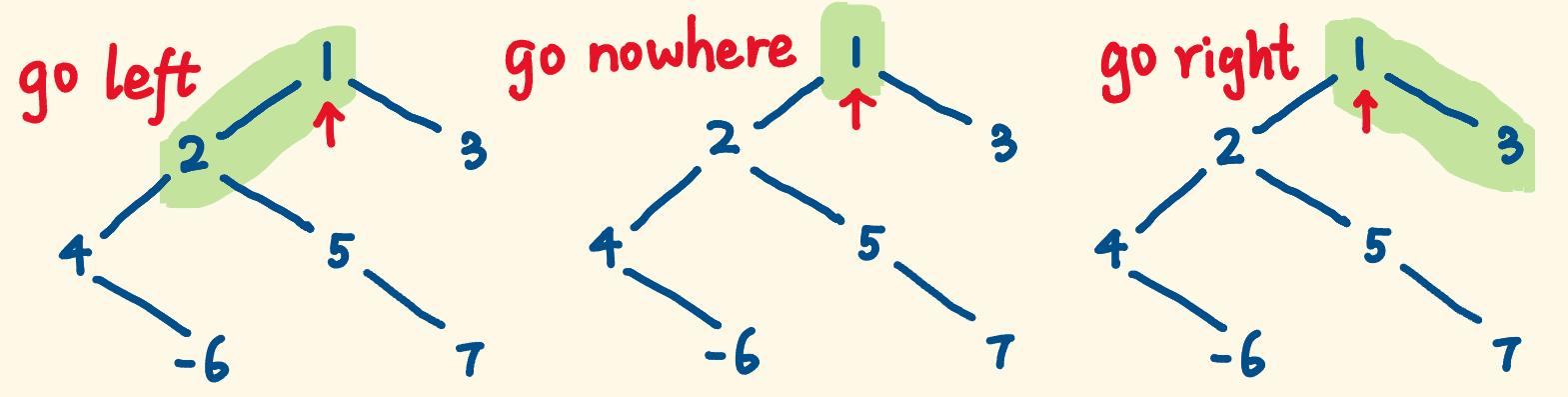
• 路径每到一个节点，有 3 种选择：1. 停在当前节点。2. 走到左子节点。3. 走到右子节点。
• 走到子节点，又面临这 3 种选择，递归就是用来处理这种规模不一样的相同问题。
• 注意，不能走进一个分支又掉头回来走另一个分支，路径会重叠，不符合定义。
  
  定义递归函数
• 对于一个节点而言，它关心自己走入一个子树，能从中捞取的最大收益，不用管具体怎么走。
• 定义dfs函数：返回当前子树能向父节点“提供”的最大路径和。即，一条从父节点延伸下来的路径，能在当前子树中获得的最大收益。分为三种情况：
  1.路径停在当前子树的根节点，在这个子树中收益：root.val
  2.走入左子树，在这个子树中的最大收益：root.val + dfs(root.left)
  3.走入右子树，在这个子树中的最大收益：root.val + dfs(root.right)
• 对应了前面所讲，对父节点而言的三种选择，最大收益取最大值：root.val + max(dfs(root.left), dfs(root.right))
• 再次提醒: 一条从父节点延伸下来的路径，不能走入左子树又掉头走右子树，不能两头收益，路径会重叠。
• 当遍历到null节点时，null 子树提供不了收益，返回 0
• 如果某个子树 dfs 结果为负，走入它，收益不增反减，该子树应被忽略，杜绝选择走入它的可能，让它返回 0，像null一样如同砍掉。
  
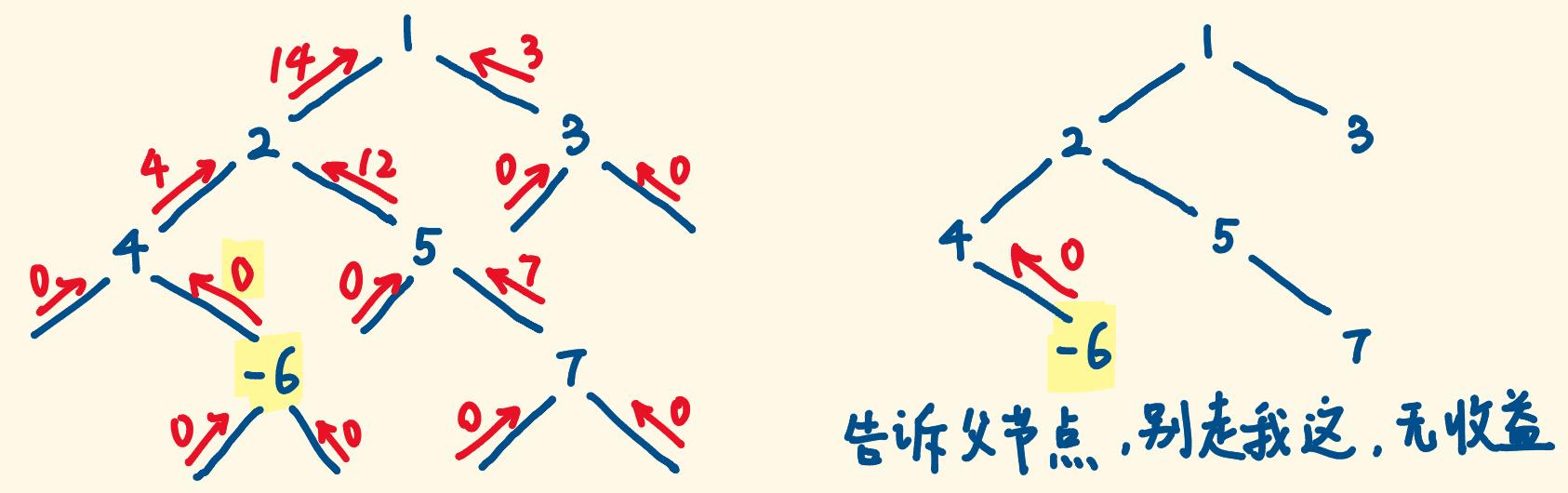
  子树中的内部路径要包含根节点
• 由题意可知，最大路径和可能产生于局部子树中，如下图左一。所以每递归一个子树，都求一下当前子树内部的最大路径和，见下图右一，从中比较出最大的。
• 注意: 一个子树内部的路径，要包含当前子树的根节点。如果不包含，那还算什么属于当前子树的路径，那就是当前子树的子树的内部路径了。
• 所以，一个子树内部的最大路径和 = 左子树提供的最大路径和 + 根节点值 + 右子树提供的最大路径和。即 dfs(root.left) + root.val + dfs(root.right)

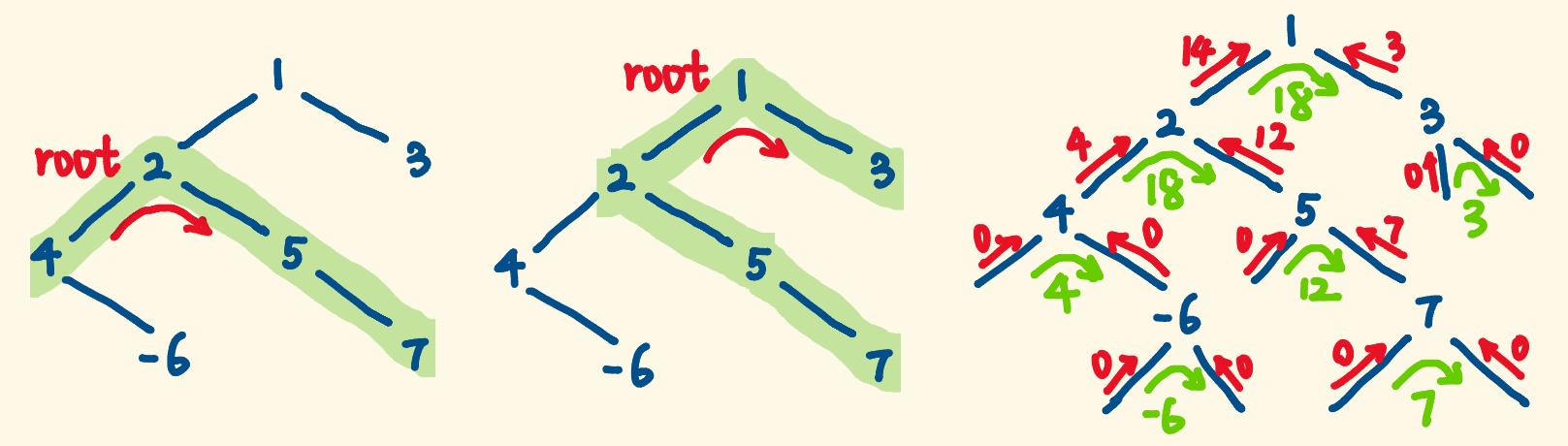
总结:

• 递归一个树，会对每个子树做同样的事（你写的处理逻辑）。
• 通过求出每个子树对外提供的最大路径和（return出来给父节点），从递归树底部向上，求出每个子树内部的最大路径和，后者是求解的目标，它的求解需要子树提供的值，理解清楚二者的关系。
• 每个子树的内部最大路径和，都挑战一下最大纪录，递归结束时，最大纪录就有了。
• 思考递归问题，不要纠结细节实现，结合求解的目标，自顶而下、屏蔽细节地思考。随着递归出栈，子问题自下而上地解决，最后解决了整个问题，内部细节是子递归帮你去做的。
• 你要做的只是写好递归的处理逻辑，怎么处理当前子树？需要返回东西吗？返回什么？再设置好递归的出口。其实就是——正确定义递归函数。
• 没有思路的时候，试着画画递归树找思路。即便做对了，画图也能加深理解。