leetcode 53. 最大子序和

Posted 2021-05-16 大忽悠爱忽悠

1.动态规划

• 这题是让求最大的连续子序和，如果不是连续的非常简单，只需要把所有的正数相加即可。但这里说的是连续的，中间可能掺杂负数，如果求出一个最大子序和在加上负数肯定要比原来小了。解这题最简单的一种方式就是使用动态规划。

我们先来了解一下动态规划的几个步骤：
1，确定状态

2，找到转移公式

3，确定初始条件以及边界条件

4，计算结果。

• 最后一个不用看，只看前3个就行，因为前3个一旦确定，最后一个结果也就出来了。我们试着找一下

1，定义dp[i]表示数组中前i+1（注意这里的i是从0开始的）个元素构成的连续子数组的最大和。
2，如果要计算前i+1个元素构成的连续子数组的最大和，也就是计算dp[i]，只需要判断dp[i-1]是大于0还是小于0。如果dp[i-1]大于0，就继续累加，dp[i]=dp[i-1]+num[i]。如果dp[i-1]小于0，我们直接把前面的舍弃，也就是说重新开始计算，否则会越加越小的，直接让dp[i]=num[i]。所以转移公式如下：dp[i]=num[i]+max(dp[i-1],0);
3，边界条件判断，当i等于0的时候，也就是前1个元素，他能构成的最大和也就是他自己，所以dp[0]=num[0];

找到了上面的转移公式，代码就简单多了，来看下

class Solution {
public:
	int maxSubArray(vector<int>& nums) 
	{
		int len = nums.size();
		int* dp = new int[len];
		dp[0] = nums[0];
		int Max = dp[0];
		for (int i = 1; i < len; i++)
		{
			dp[i] = max(dp[i - 1], 0) + nums[i];
			Max = max(Max, dp[i]);
		}
		return Max;
	}
};

代码优化：

• 仔细看下上面的代码会发现，我们申请了一个长度为length的数组，但在转移公式计算的时候，每次计算当前值的时候只会用到前面的那个值，再往前面就用不到了，这样实际上是造成了空间的浪费。这里不需要一个数组，只需要一个临时变量即可，看下代码：

class Solution {
public:
	int maxSubArray(vector<int>& nums) 
	{
		int len = nums.size();
		int cur = nums[0];
		int Max = cur;
		for (int i = 1; i < len; i++)
		{
			cur = max(cur, 0) + nums[i];
			Max = max(Max, cur);
		}
		return Max;
	}
};

2.暴力求解

• 比较容易想到的是用“暴力解法”做，即穷举所有的子区间。思路虽然简单，但是写好暴力解法也不是一件容易的事情。
• 使用双层循环，穷举所有的子区间；
• 然后再对子区间内的所有元素求和；
• 时间复杂度是立方级别的。

int addSum(vector<int>& nums, int left, int right)
{
	int res = 0;
		for(int i = left; i <= right; i++)
			res += nums[i];
		return res;
}
class Solution {
public:
	int maxSubArray(vector<int>& nums) 
	{
		int len = nums.size();
		int cur=nums[0], Max=cur;
		for (int i = 0; i < len; i++)
		{
			for (int j = 0; j <=i; j++)
			{
				cur=addSum(nums,j,i);
				Max = max(cur, Max);
			}
		}
		return Max;
	}
};

• 优化：事实上，上面的代码有一些重复计算。这是因为相同前缀的区间求和，可以通过类似“状态转移”的方法得到。
• 例如：计算子区间 [1, 4] 的和可以在计算子区间 [1, 3] 的基础上，再加上 nums[4] 得到。
• 因此，只需要枚举子序的左端点，然后再扫描右端点，就可以减少一个级别的复杂度。

class Solution {
public:
	int maxSubArray(vector<int>& nums) 
	{
		int len = nums.size();
		int Max = nums[0];
		for (int i = 0; i < len; i++)//这里i是子序列起始点
		{
			int sum = 0;
			for (int j = i; j <len; j++)//j是子序列结束点
			{
				sum += nums[j];
				Max = max(Max, sum);
			}
		}
		return Max;
	}
};

3.分治法

• 分治法的思路是这样的，其实也是分类讨论。
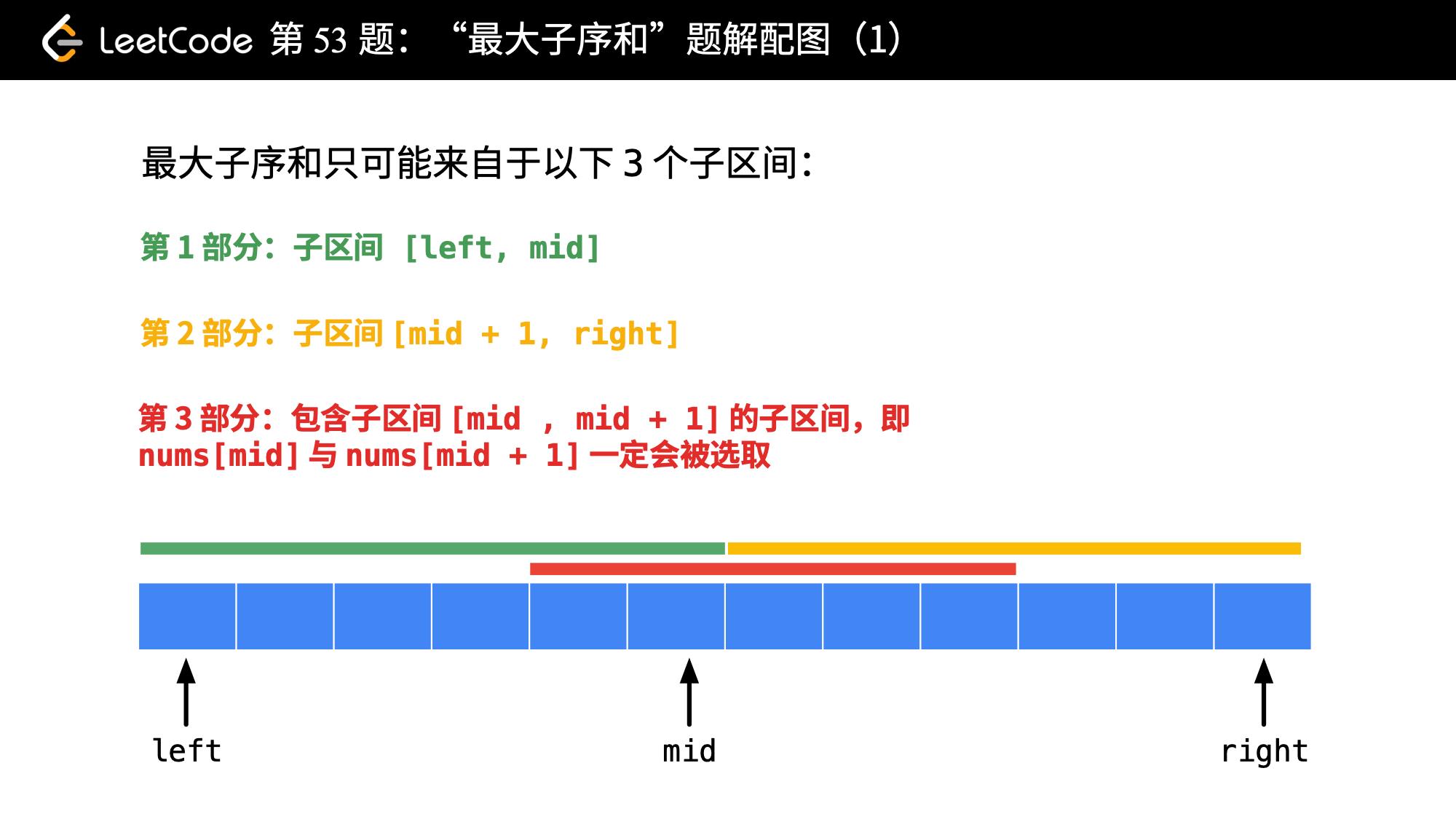
• 连续子序列的最大和主要由这三部分子区间里元素的最大和得到：

第 1 部分：子区间 [left, mid]；
第 2 部分：子区间 [mid + 1, right]；
第 3 部分：包含子区间 [mid, mid + 1] 的子区间，即 nums[mid] 与 nums[mid + 1] 一定会被选取。

• 对这三个部分求最大值即可。
  

class Solution {
public:
	int maxSubArray(vector<int>& nums) 
	{
		int len = nums.size();
		if (len == 0)
			return 0;
		return maxSubArraySum(nums,0,len-1);
	}
	int maxSubArraySum(vector<int>& nums,int left,int right)
	{
		//如果子序列中只有一个值，那么当前子序列最大值就是当前值本身
		if (left == right)
			return nums[left];
		//计算当前序列的中间位置
		int mid = (left + right) / 2;
		//计算左半部分子序列中包含的最大子序列长度，右半部分子序列中包含的最大子序列长度，
		//和整个序列的长度中最大子序列长度，取最大值
		return MAX(maxSubArraySum(nums, left, mid), maxSubArraySum(nums, mid + 1, right),maxCrossingSum(nums,left,mid,right));
	}
	//计算三个数中的最大值
	int MAX(int num1, int num2, int num3)
	{
		return max(num1, max(num2,num3));
	}
	//计算整个序列长度中最大子序列长度，该最长子序列必须包含mid位置
	int maxCrossingSum(vector<int>& nums,int left,int mid,int right)
	{
		int sum = 0;
		int leftSum = -2147483648;//这里也可以写成：int leftSum = nums[mid];
		//左半边包含mid位置的元素，那么左半边的最大子序列和为多少呢？
		for (int i = mid; i >= left; i--)
		{
			sum += nums[i];
			if (sum > leftSum)
				leftSum = sum;
		}
		sum = 0;
		int rightSum = -2147483648;//这里也可以写成:	int rightSum = nums[mid+1];
		//右半边不包含mid位置的元素，那右半部分的最大子序列和为多少呢？
		for (int i = mid + 1; i <= right; i++)
		{
			sum += nums[i];
			if (sum > rightSum)
				rightSum = sum;
		}
		return rightSum + leftSum;
	}
};

4.贪心算法
贪心贪的是哪里呢？

• 如果 -2 1 在一起，计算起点的时候，一定是从1开始计算，因为负数只会拉低总和，这就是贪心贪的地方！
• 局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。
• 全局最优：选取最大“连续和”
  局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。

class Solution {
public:
	int maxSubArray(vector<int>& nums) 
	{
		int MAX = nums[0];
		int count = 0;
		for (int i = 0; i < nums.size(); i++)
		{
			count += nums[i];
			MAX = max(MAX, count);
			count = max(count, 0);
		}
		return MAX;
	}

};