leetcode 931. 下降路径最小和

Posted 2021-05-16 大忽悠爱忽悠

---

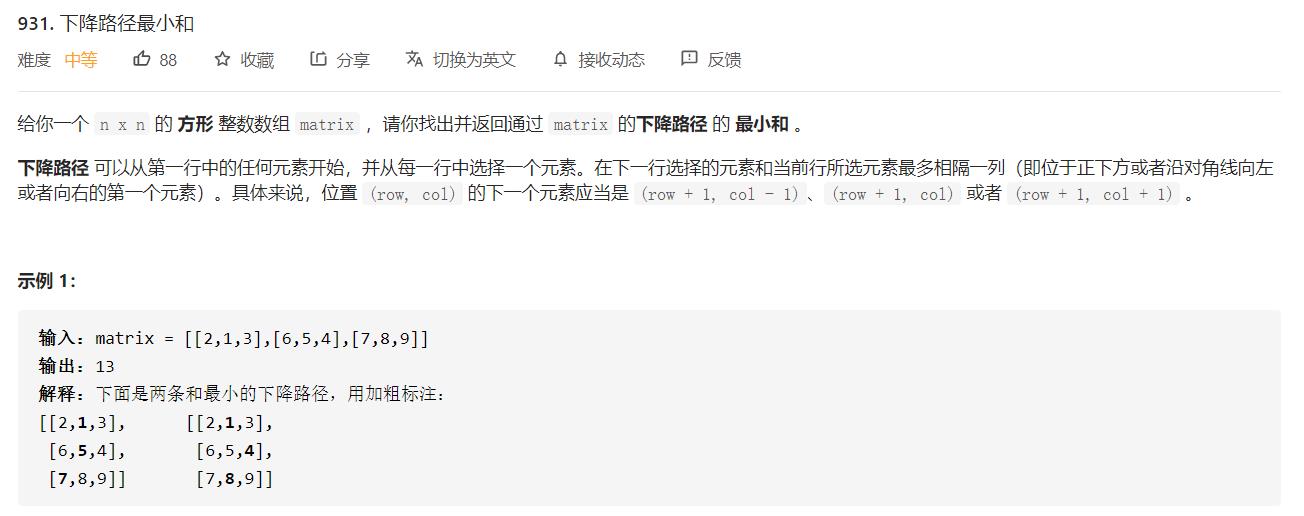
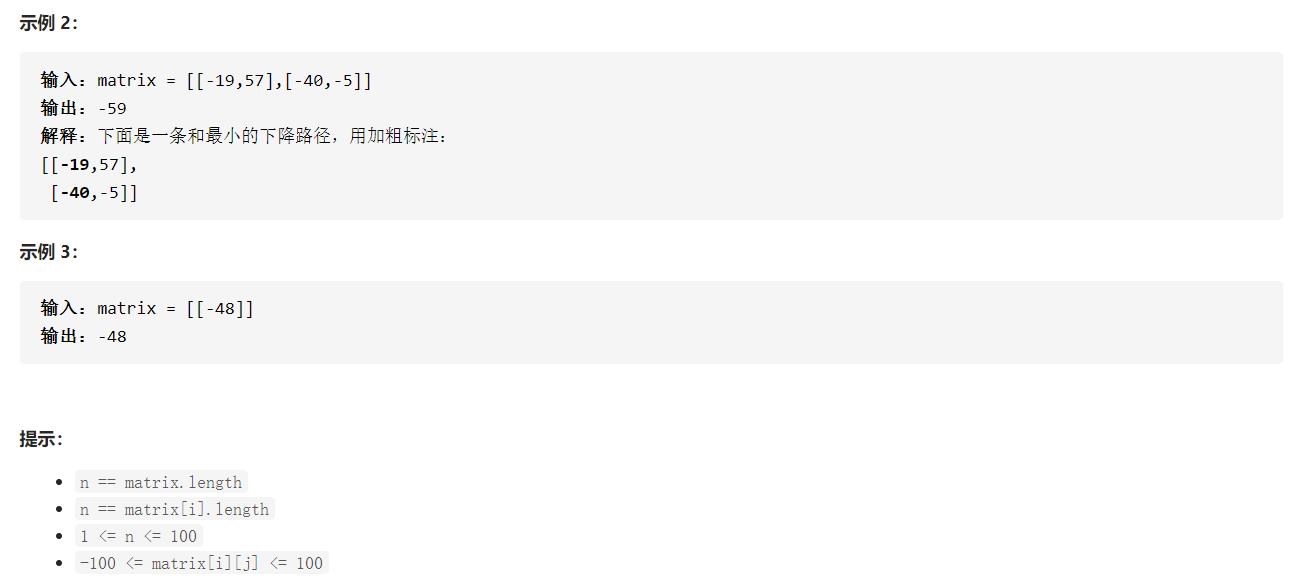
下降路径最小和题解汇总

• 自上而下的动态规划
• 自下而上的动态规划
• 动态规划的优化---一维数组
• 记忆化递归

---

自上而下的动态规划

• 矩阵中的动态规划基本上都比较容易入手。这道题也算是入门题，我们可以设dp[i][j]表示到(i,
  j)位置的最小和，通过题目描述和手动模拟我们很容易得出状态转移方程：
• dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+A[i][j]
• 最后取dp最后一行的最小值即可
  
• 对于这种需要考虑边界的情况，我习惯在原数组的基础上套一层"壳"，这样状态转移的时候就不用特判边界了。
  

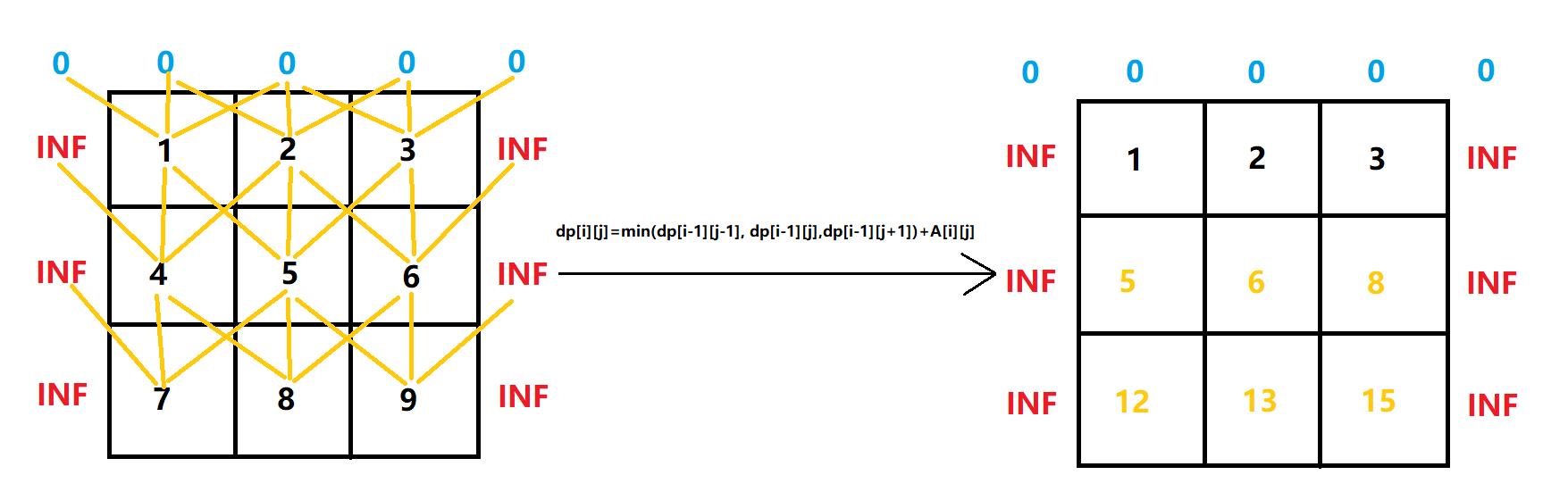
class Solution {
public:
	int minFallingPathSum(vector<vector<int>>& matrix) 
	{
		if (matrix.empty()) return 0;
		int r = matrix.size();
		vector<vector<int>> dp(r + 1, vector<int>(r + 2,0));
		//套壳处理---两边均为最大值
		for (int i = 0; i < r+1; i++)
		{
			dp[i][0] = INT_MAX;
			dp[i][r+1] = INT_MAX;
		}
		for (int i = 1; i <r+1; i++)
		{
			for (int j = 1; j < r+1; j++)
			{
				dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i-1][j-1];
			}
		}
		int Min = INT_MAX;
		for (int i = 0; i < r + 2; i++)
			Min = min(Min, dp[r][i]);
		return Min;
	}
};  

---

自下而上的动态规划

动态规划解题三部曲:

• 1.定义dp[i][j]数组的含义：

• 当前位置(i,j)对应的上升位置最小和，注意这里是自下而上的动态规划，因此是上升位置的最小和

• 2,找出数组元素之间的关系式：

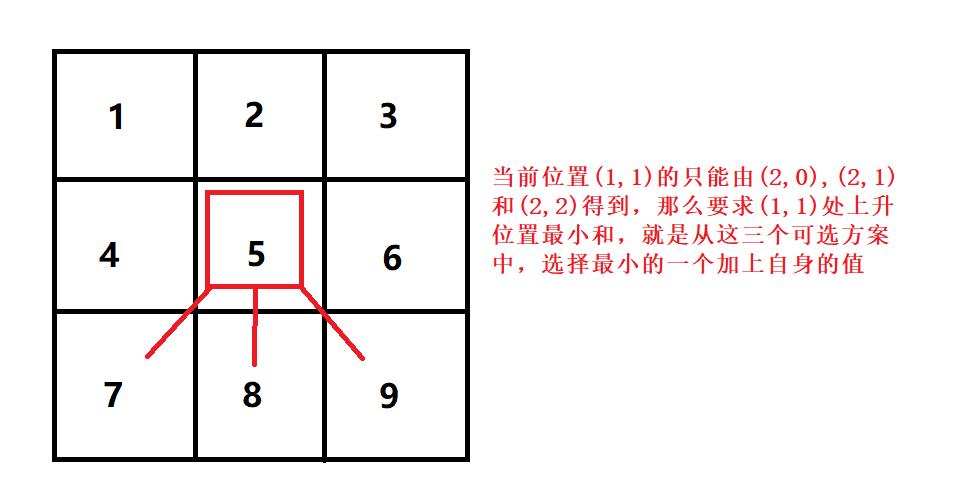
• 根据题目中所说位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1)
  

• 因此我们得到了状态转移方程：

• dp[i][j] = min(dp[i + 1][j], min(dp[i + 1][j + 1],dp[i+1][j-1])) + matrix[i][j];

• 但是注意考虑特殊情况:

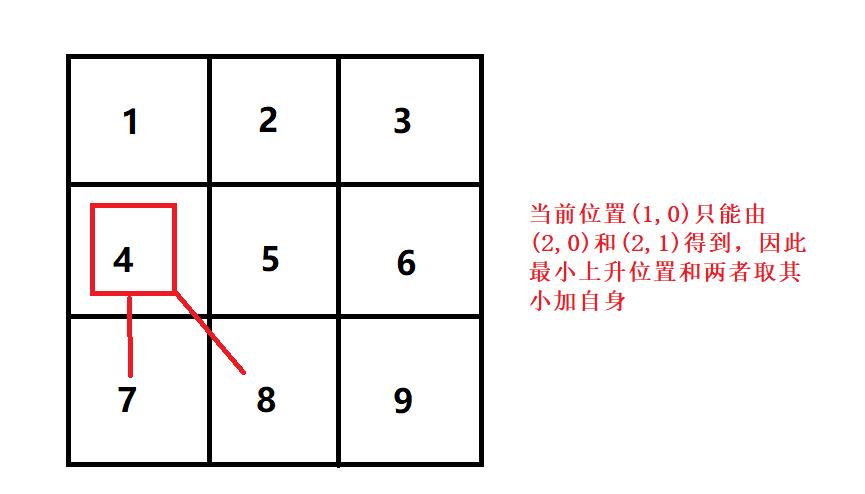
• 1.当前位置为最左边一列的时候
  

• 此时对应的状态转移方程:

• dp[i][j] = min(dp[i + 1][j], dp[i + 1][j + 1]) + matrix[i][j];

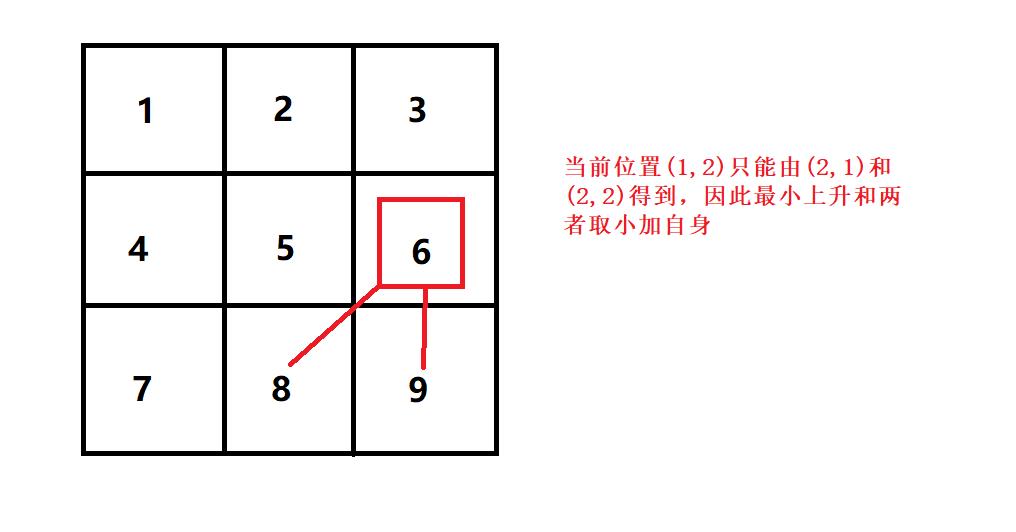
• 2,当前位置为最右边一列的时候
  

• 此时对应的状态转移方程:

• dp[i][j] = min(dp[i + 1][j], dp[i + 1][j - 1]) + matrix[i][j];

• 这里我们给dp数组多添加一行

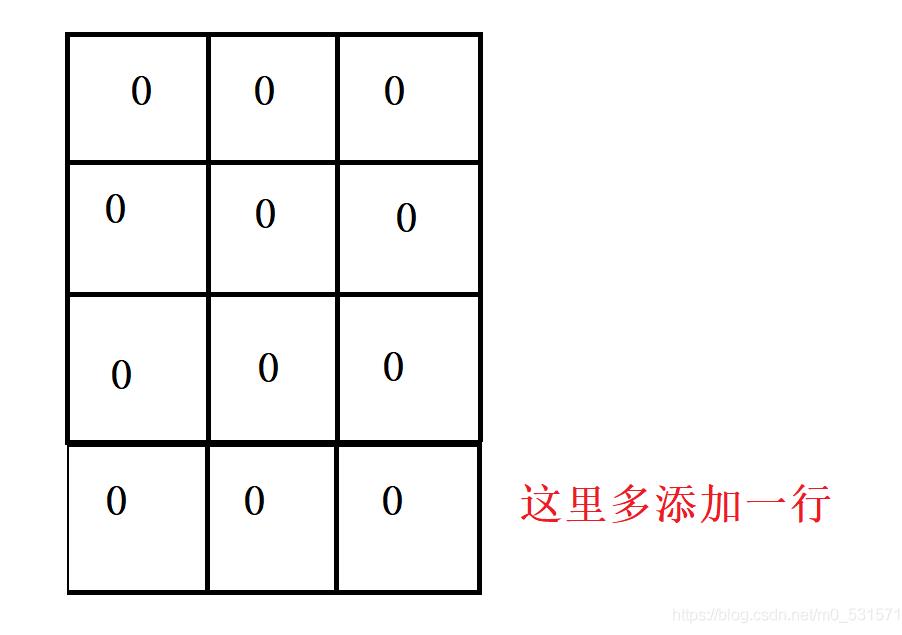
添加一行后，最后一行的每个元素最小值就是0，不需要求解

• 如果没添行的话，我们需要提前求出dp数组最后一行的最小值，这样的话，最后一行的求法就不满足状态转移方程了：
  

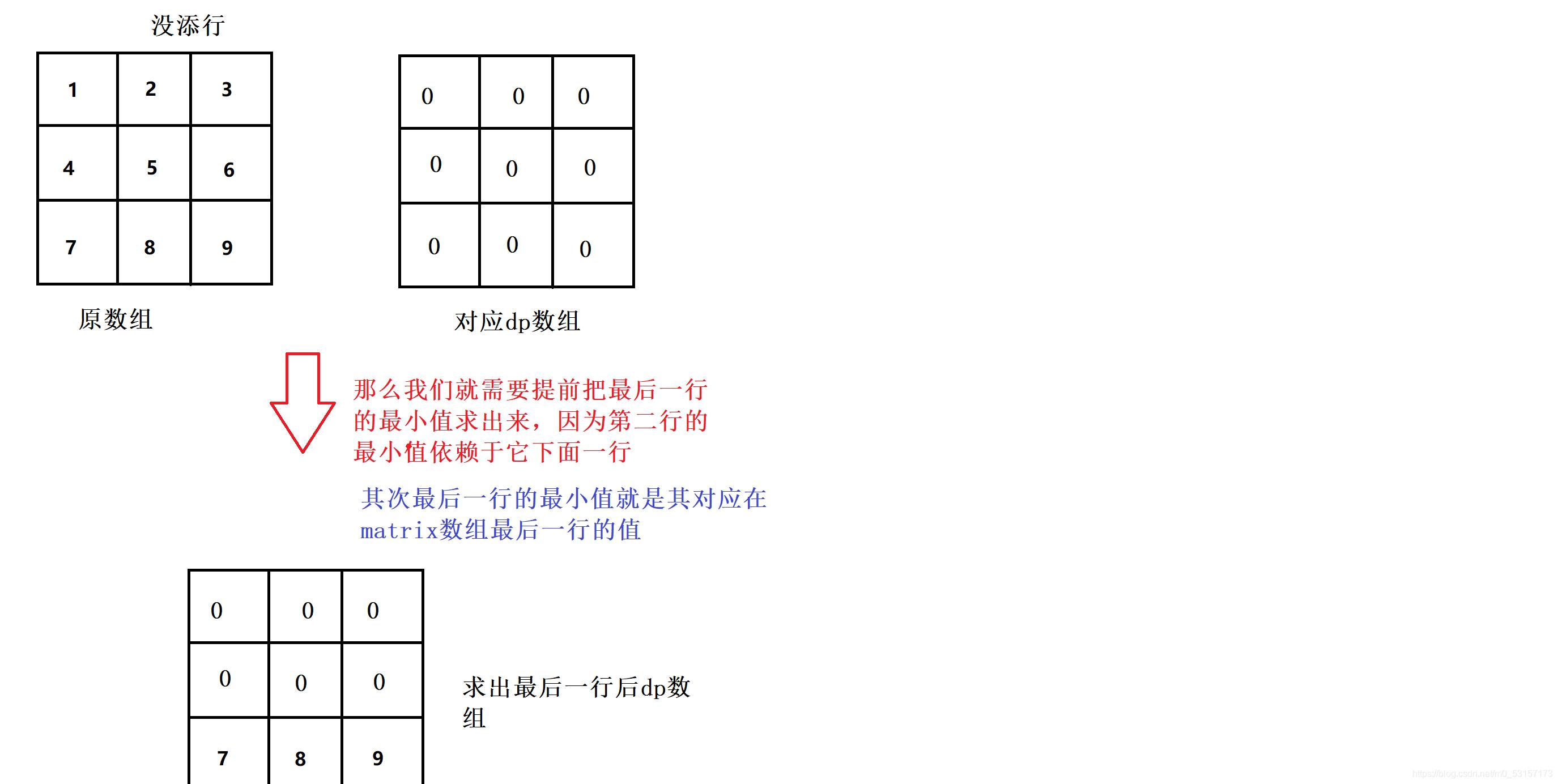
总结:没添行与添加行后的区别

• 没添行的话需要提前求出最后一行的dp值，对应的就是matrix的最后一行的值
• 添行后，原来最后一行的求法也满足状态转移方程，并且新的最后一行的最小值就是0

添行的代码:

class Solution {
public:
	int minFallingPathSum(vector<vector<int>>& matrix) 
	{
		if (matrix.empty()) return 0;
		if (matrix.size() == 1) return matrix[0][0];
		int r = matrix.size();
		int c = matrix[0].size();
		vector<vector<int>> dp(r+1, vector<int>(c,0));
		for (int i = r-1; i >= 0; i--)
		{
			for (int j = c-1; j >= 0; j--)
			{
				if (j == c - 1)
					dp[i][j] = min(dp[i + 1][j], dp[i + 1][j - 1]) + matrix[i][j];
				else if (j == 0)
					dp[i][j] = min(dp[i + 1][j], dp[i + 1][j + 1]) + matrix[i][j];
				else
				  dp[i][j] = min(dp[i + 1][j], min(dp[i + 1][j + 1],dp[i+1][j-1])) + matrix[i][j];
			}
		}
		int Min = INT_MAX;
		for (int i = 0; i < c; i++)
			Min = min(dp[0][i], Min);
		return Min;
	}
};

没添行的代码:

class Solution {
public:
	int minFallingPathSum(vector<vector<int>>& matrix) 
	{
		if (matrix.empty()) return 0;
		if (matrix.size() == 1) return matrix[0][0];
		int r = matrix.size();
		int c = matrix[0].size();
		vector<vector<int>> dp(r, vector<int>(c,0));
		for (int i = 0; i < c; i++)//求解最后一行的dp值
			dp[r - 1][i] = matrix[r - 1][i];
		for (int i = r-2; i >= 0; i--)
		{
			for (int j = c-1; j >= 0; j--)
			{
				if (j == c - 1)
					dp[i][j] = min(dp[i + 1][j], dp[i + 1][j - 1]) + matrix[i][j];
				else if (j == 0)
					dp[i][j] = min(dp[i + 1][j], dp[i + 1][j + 1]) + matrix[i][j];
				else
				  dp[i][j] = min(dp[i + 1][j], min(dp[i + 1][j + 1],dp[i+1][j-1])) + matrix[i][j];
			}
		}
		int Min = INT_MAX;
		for (int i = 0; i < c; i++)
			Min = min(dp[0][i], Min);
		return Min;
	}
};

• 在这里添行法没有展现太大的优势，但在有些时候却能大大节省计算量，可以参照leetcode 120. 三角形最小路径和

---

动态规划的优化—一维数组

• 因为这里计算第i行的值只与第i-1行有关，因此我们可以用滚动数组的思想简化为一维数组

• 看图：
  

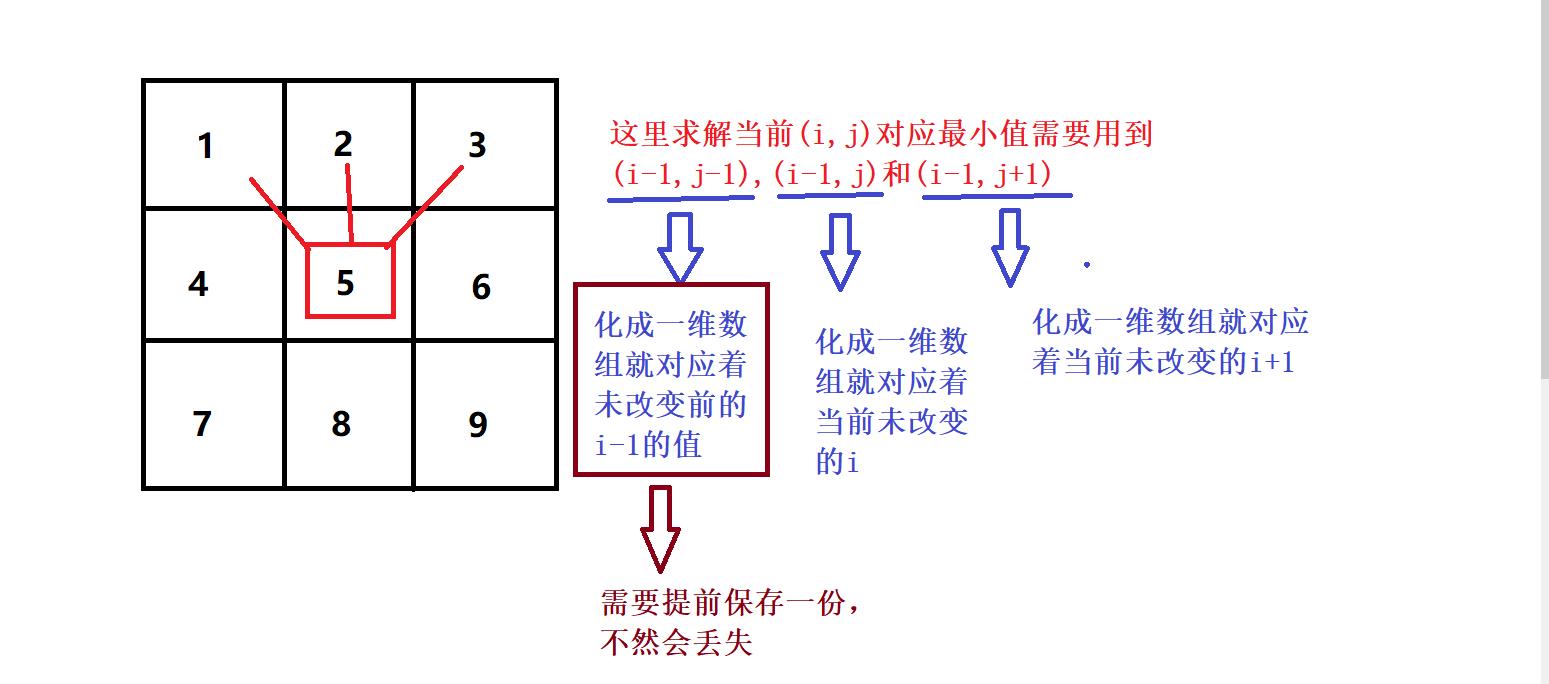
• 这里还是采用法1自上而下的动态套壳法，免去边界计算的问题
  

class Solution {
public:
	int minFallingPathSum(vector<vector<int>>& matrix) 
	{
		if (matrix.empty()) return 0;
		int r = matrix.size();
		vector<int> dp(r + 2,0);//实际有效值范围1---r
		//初始值---第一行数据初始化
		for (int i = 1; i < r + 1; i++)
		{
			dp[i] = matrix[0][i-1];
		}
		//套壳处理---两边均为最大值
			dp[0] = INT_MAX;
			dp[r+1]= INT_MAX;
		//从第二行开始处理
		for (int i = 1; i <r; i++)
		{
			int pre = INT_MAX;
			//从每一行第二个元素开始处理，处理元素范围1---r
			for (int j = 1; j <r+1; j++)
			{
				//保存(i-1,j-1)
				int temp = dp[j];
				dp[j] = min(pre, min(dp[j], dp[j + 1])) + matrix[i][j-1];
				pre = temp;
			}
		}
		int Min = INT_MAX;
		//最小值只可能出现在1---r范围内
		for (int i = 1; i <=r; i++)
		{
			Min = min(Min, dp[i]);
		}
		return Min;
	}
};

---

记忆化递归

class Solution {
	map<pair<int, int>, int>  map;//记录当前位置的结果是否求出
	vector<vector<int>> m;
public:
	int minFallingPathSum(vector<vector<int>>& matrix) 
	{
		if (matrix.empty()) return 0;
		int r = matrix.size();
		this->m = matrix;
		//选择出最后一行中的最小值
		int Min = INT_MAX;
		for (int j = 0; j < r; j++)
		{
			Min = min(Min, dp(r - 1, j));
		}
		return Min;
	}
	//返回当前位置的结果
	int dp(int i,int j)
	{
		//越界就返回
		if (i < 0 || j < 0 || i >= m.size() || j >= m[0].size())
			return INT_MAX;
		//最小子结果---第一行的任何位置的结果可以直接求出
		if (i == 0)
			return m[i][j];
		//查找备忘录防止重复计算
		if (map.find({ i,j }) != map.end())
			return map[{i, j}];
		//将当前位置的结果存入map容器中
		map[{i, j}] = m[i][j] + min(
			dp(i - 1, j), // 上
			min(dp(i - 1, j - 1), // 左上
			dp(i - 1, j + 1)) // 右上
		);
		//返回当前位置的结果
		return map[{i, j}];
	}
};