C++ 实现带权有向图的单源点最短路径Dijkstra算法(完整代码)

Posted 2021-05-08 Wecccccccc

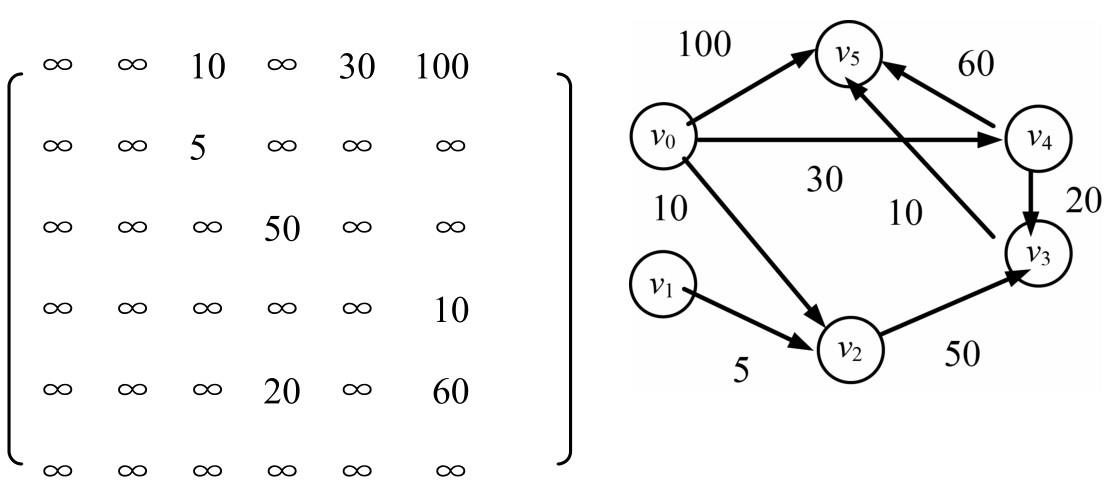
首先，引进一个辅助向量D，它的每个分量D[i]表示当前所找到的从始点v0到每个终点vi的最短路径的长度。

它的初态为：若从v0到vi有弧，则D[i]为弧上的权值；否则，置D[i]为∞。

显然，长度为
D[j]=Min{D[i]|vi∈V-S}, S初值为{v0}
的路径就是从v0出发的长度最短的一条路径。
此路径为（v0, vj）。

那么，下一条长度次短的路径是哪一条呢？
假设该次短路径的终点是vk，可想而知，这条路径或者是（v0, vk），或者是（v0, vj, vk）。

它的长度或者是从v0到vk的弧上的权值，或者是D[j]和从vj到vk的弧上的权值之和。

在一般情况下，下一条长度次短的路径的长度必是
D[j]=Min{D[i]|vi∈V-S}
其中，D[i]或者是弧（v0, vi）上的权值，或者是D[k]（vk∈S和弧（vk, vi）上的权值之和。

根据以上分析，可以得到如下描述的算法。

1. 假设用带权的邻接矩阵arcs表示带权有向图，arcs[i][j]表示弧〈vi, vj〉上的权值。

   若〈vi, vj〉不存在，则置arcs[i][j]为∞（在计算机上可用允许的最大值代替）。

   S为已找到从v0出发的最短路径的终点的集合，它的初始状态S={v0}。

   那么，从v0出发到图上其余各顶点vi可能达到最短路径长度的初值为 D[i]=arcs[LocateVertex(G,v0)][i],
   vi∈V-S

2. 选择vj，使得 D[j]=Min{D[i]|vi∈V-S} vj就是当前求得的一条从v0出发的最短路径的终点。令S=S∪{vj}。

3. （3）修改从v0出发到集合V-S上任一顶点vk可达的最短路径长度。如果 D[j]+arcs[j][k]<D[k] 则修改D[k]为
   D[k]=D[j]+arcs[j][k] 重复操作步骤（2）和步骤（3）共n-1次。

由此求得从v0到图上其余各顶点的最短路径是依路径长度递增的序列。

用C++语言描述的Dijkstra算法如下:

#include <iostream>
using namespace std;

const int MAXW = 30000;
const int MaxVertexNum = 30;
typedef int VertexType;
class MGraph
{
public:
	void CreateGraph();
	void ShortestPath_Dij(int v0);
	void Print_Path_Dij(int v0);

private:
	int vertexnum;
	VertexType vertexs[MaxVertexNum];
	int edgenum;
	int P[MaxVertexNum];
	int D[MaxVertexNum];
	int arcs[MaxVertexNum][MaxVertexNum];
};

void MGraph::CreateGraph()
{
	cout << "请输入节点数和边条数" << endl;
	cin >> vertexnum >> edgenum;
	for (int i = 0; i < vertexnum; i++)
		for (int j = 0; j < vertexnum; j++)
			arcs[i][j] = MAXW;
	cout << "请依次输入按序号0到n顶点的中存储的信息" << endl;
	for (int i = 0; i < vertexnum; i++)
	{
		cin >> vertexs[i];
	}
	cout << "下面输入边的信息" << endl;
	for (int i = 0; i < edgenum; i++)
	{
		int v1, v2, w;
		cout << "输入边<i,j>对应的顶点序号i,j,然后再输入该边的权值" << endl;
		cin >> v1 >> v2 >> w;
		arcs[v1][v2] = w;
	}
}

void MGraph::ShortestPath_Dij(int v0)
{
	bool f[MaxVertexNum];
	for (int v = 0; v <vertexnum; v++)
	{
		f[v] = false;
		D[v] = arcs[v0][v];
		P[v] = -1;
		if (D[v] < MAXW) P[v] = v0;
	}
	D[v0] = 0;
	f[v0] = true;
	for (int i = 0; i < vertexnum; i++)
	{
		int v = -1;
		int min = MAXW;
		for (int w = 0; w < vertexnum; w++)
			if (!f[w] && D[w] < min)
			{
				v = w;
				min = D[w];
			}
		if (v == -1) break;
		f[v] = true;
		for (int w = 0; w < vertexnum; w++)
		{
			if (!f[w] && (min + arcs[v][w] < D[w]))
			{
				D[w] = min+arcs[v][w];
				P[w] = v;
			}
		}
	}
}


void MGraph::Print_Path_Dij(int v0)
{
	cout << "The shortest path from Vertex:" << v0 << " to the other Vertex:" << endl;
	for (int v = 0; v < vertexnum; v++)
	{
		if (P[v] == -1)continue;
		cout << D[v] << " ";
		cout << v << "<=";
		int i = v;
		while (P[i] != -1)
		{
			cout << P[i] << "<=";
			i = P[i];
		}
		cout << endl;
	}
}


int main()
{
	MGraph g;
	g.CreateGraph();
	int v0;
	cin >> v0;
	g.ShortestPath_Dij(v0);
	g.Print_Path_Dij(v0);
	return 0;
}

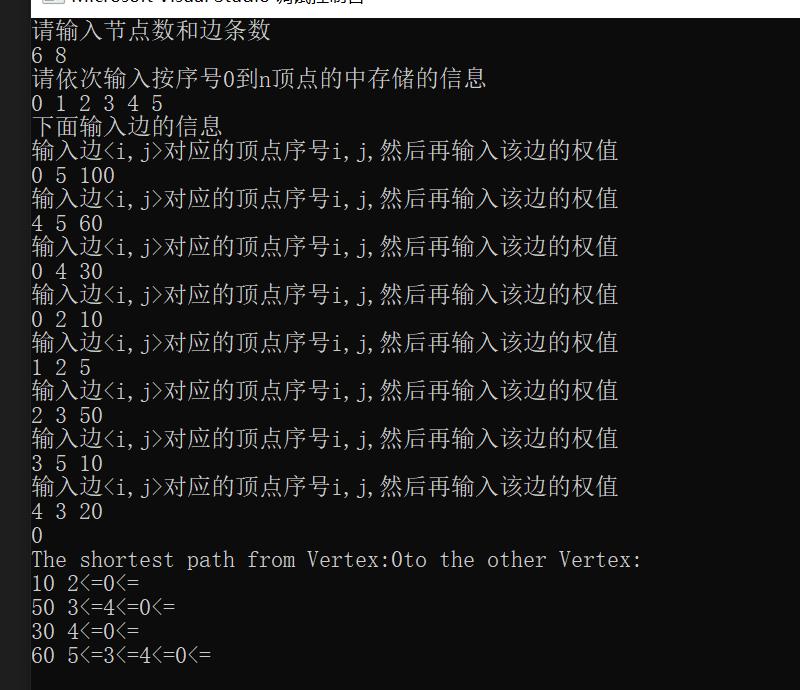
测试结果: