二叉树的遍历方式到底有多少种

Posted 2021-05-03 航哥说JAVA

最近有一个朋友在学习群里面说，在面试的时候，面试官给了一张纸，让他尽可能地写出二叉树的遍历方式，那么二叉树的遍历方式到底有多少种呢？

我们都知道二叉树是一个很基本的数据结构，是红黑树的爷爷辈，是二叉搜索树的父辈，所以这个考察如果你答得不好，面试官基本会锁定你对整个“树”体系都不太熟悉。

那么二叉树的遍历方式到底有几种呢？

答案是五种，分别是，前序遍历、中序遍历、后序遍历、层次遍历和之字形遍历。前三种广泛地用于各种树类型解题操作中，可以说是树类型的最基本操作。

我们先说说前、中、后序遍历。

这个前、中、后值得是当前节点的输出顺序，它最前输出，就是前序；先输出它的左子节点就是中序；先输出左子节点、再输出右子节点，最后才输出当前节点就是后序遍历。

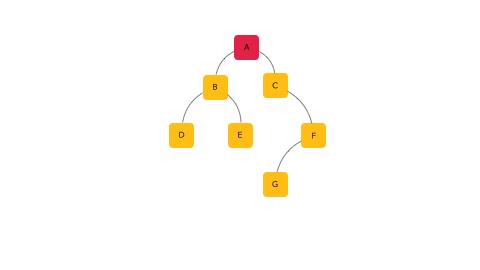
比如我有一个二叉树

前序遍历的顺序就是  A - B - D - E - C - F - G

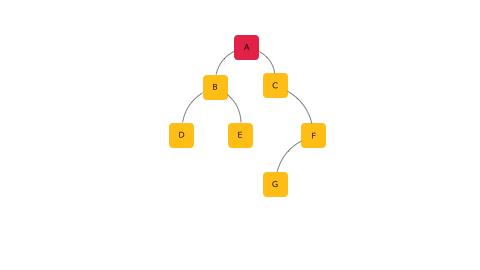
中序遍历的顺序就是 D - B - E - A - C - G - F

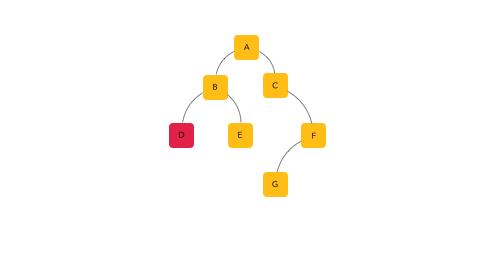
后序遍历的顺序就是 D - E - B - G - F - C - A 

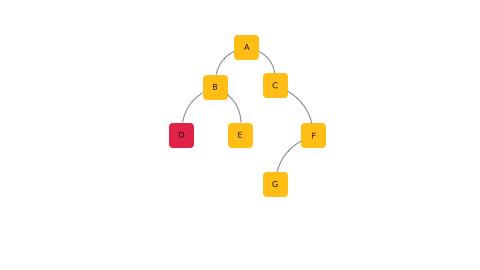
总之就是：

前序遍历，当前节点的输出，一定在任意一个左子树上的节点，或者右子树上的节点之前。

中序遍历，一定是当前节点的左子树的所有节点输出完了，再输出当前节点，再输出右子树上的所有节点。

后序遍历，一定是，当前节点的左子树的所有节点全都输出完了，右子树的所有节点也输出完了，才输出当前节点（所以根节点永远最后输出）

这三种的实现方式的代码很简单，其中res是为了记录遍历结果使用的。

   

/** * 前序遍历 */ PRE_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.nonNull(root)) { res.add(root.val); order(root.left, res); order(root.right, res); } return res; } }, /** * 中序遍历 */ IN_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.nonNull(root)) { order(root.left, res); res.add(root.val); order(root.right, res); } return res; } }, /** * 后序遍历 */ POST_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.nonNull(root)) { order(root.left, res); order(root.right, res); res.add(root.val); } return res; } }

那么，层次遍历就是遍历顺序是从第一层开始从左到右打印，而后第二层从左到右，直到最后一层。

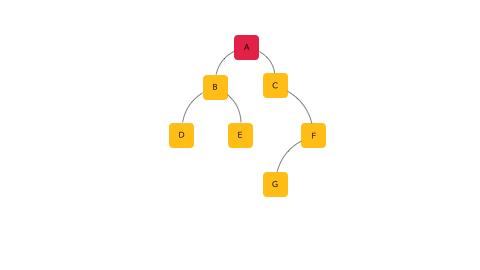
之字形，顾名思义，就是要第一层是从左到右，第二层就要从右到左。

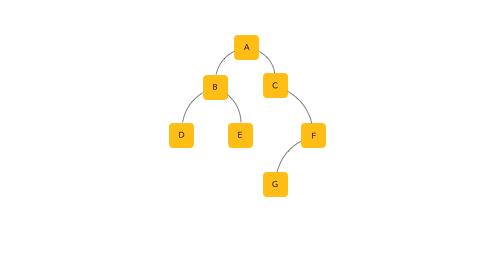
要实现这两种遍历方式，我们需要两个容器，一个是队列，一个是栈。

队列是一个先进先出的数据结构，我们遍历第一层的时候把他们的左右子节点（也就是）依次放入到一个队列中，等遍历第二层的时候，就从那个队列中依次取出队列中的节点，再把它们的左右子节点依次的放入另外一个队列中，这样来回操作就可以实现层次遍历。

而之字形，就是先进去的孩子节点要在之后的遍历中后出来，所以我们想到的就是栈，在遍历第一层的时候，先放到一个栈里面，然后取出栈中的元素，把他的左右子节点依次放入另外一个栈中，这样，栈里面出的顺序就是倒序的，然后第三次的时候依次放入右子节点和左子节点，这样取出的时候就是从第三排左边开始弹栈。这样来回操作，即可实现之字形遍历。具体实现过程大家可以自行画图模拟，有问题也可给我留言。

五种遍历完整代码如下，笔者将其封装到了一个枚举中。

/** * 二叉树遍历方式枚举类 */enum TraverseWayEnum { /** * 前序遍历 */ PRE_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.nonNull(root)) { res.add(root.val); order(root.left, res); order(root.right, res); } return res; } }, /** * 中序遍历 */ IN_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.nonNull(root)) { order(root.left, res); res.add(root.val); order(root.right, res); } return res; } }, /** * 后序遍历 */ POST_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.nonNull(root)) { order(root.left, res); order(root.right, res); res.add(root.val); } return res; } }, /** * 层次遍历 */ LEVEL_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.isNull(root)) { return new LinkedList<>(); } Queue<TreeNode> oddQueue = new LinkedList<>(); Queue<TreeNode> evenQueue = new LinkedList<>(); oddQueue.add(root); while (!oddQueue.isEmpty() || !evenQueue.isEmpty()) { helpLevelOrder(res, oddQueue, evenQueue); helpLevelOrder(res, evenQueue, evenQueue); } return res; } }, /** * 之字形遍历 */ ZIGZAG_LEVEL_ORDER { @Override public List<Integer> order(TreeNode root, List<Integer> res) { if (Objects.isNull(root)) { return new LinkedList<>(); } Stack<TreeNode> oddStack = new Stack<>(); Stack<TreeNode> evenStack = new Stack<>(); oddStack.add(root); while (!oddStack.empty() || !evenStack.empty()) { while (!oddStack.empty()) { TreeNode pop = oddStack.pop(); if (Objects.nonNull(pop.left)) { evenStack.add(pop.left); } if (Objects.nonNull(pop.right)) { evenStack.add(pop.right); } res.add(pop.val); } while (!evenStack.empty()) { TreeNode pop = evenStack.pop(); if (Objects.nonNull(pop.right)) { oddStack.add(pop.right); } if (Objects.nonNull(pop.left)) { oddStack.add(pop.left); } res.add(pop.val); } } return res; } };

 private static void helpLevelOrder(List<Integer> res, Queue<TreeNode> oneQueue, Queue<TreeNode> secondQueue) { while (!oneQueue.isEmpty()) { TreeNode poll = oneQueue.poll(); if (Objects.nonNull(poll.left)) { secondQueue.add(poll.left); } if (Objects.nonNull(poll.right)) { secondQueue.add(poll.right); } res.add(poll.val); } }

 public abstract List<Integer> order(TreeNode root, List<Integer> res);}

以上是关于二叉树的遍历方式到底有多少种的主要内容，如果未能解决你的问题，请参考以下文章

二叉树的遍历

二叉树的四种遍历方式

通过两种深度优先遍历方式重建二叉树或者得到其余一种遍历方式

二叉树概念及其三种遍历方式实现

二叉树的三种遍历方式

图解 二叉树的四种遍历