神经网络算法实现

Posted 2021-04-24 百林哲

AlphaGo在人机大战中战胜李世乭让深度学习这个名词在大众口中广为传播，深度学习的强大，也让其增加了一层神秘色彩，似乎这是名校博士才能理解的算法。虽然相关的论文自己也无法看懂，然而，在网络查阅了无数资料之后，才发现如果不去纠结理论的证明，只关心结论的话，神经网络算法也并非高不可攀。

什么是神经网络算法

在解释什么是神经网络之前，我们先明确几个机器学习中的术语：特征，样本，监督学

• 样本：可以用于学习的个体，我们可以获得这些个体的其某些信息，并且我们已知这些个体的类别

• 特征：同一属性在不同个体所体现出来的特点，在神经网络中，特征应该是易于提取的

• 监督学习：根据样本中个体的特征以及类别，然后创建我们的判定规则，并依靠这些调查所得信息，调整我们的规则，使得规则的预测结果尽可能接近我们的样本，这样，我们利用这个规则和新个体的特征信息，来判定其所属分类

  
  

举个例子，我们想要构建一套性别识别算法，而我们能够获得的特征信息只有三种：这个人不是长头发；衣服颜色是红色；身高是否超过了178cm。那以一个正常成年人的思维，我们应该采用什么策略来判断这个人的性别呢？

我想大部分人都会采用和我一样的策略：依据我们平时的经验，一个人如果留长头发，很大可能这个人是女的，而一个人穿红色衣服，很难判断其性别，一个人身高超过175cm，在中国人里面可能都属于偏高的，而依据我们的经验，男性的平均身高要大于女性，所以单纯通过身高这个信息，我们推断这个人是男性的可能性较大。

以上推测过程中，我们对每一个条件的推断都基于一个词，经验，这里的经验就是我们长期以来观察身边的人的特征所留下的记忆。而我们的推测结果主要用了一个词汇，可能性，其代表基于某条已知信息推测出某个未知结论的概率。

科学家将我们的思维方法归纳为信息在神经元之间的传导过程，这些神经元每一个都处理及简单的信息，但是通过无数个神经元之间错综复杂的连接传导，使得我们的大脑能够处理及其复杂的信息。神经网络算法就是对我们大脑思维方式的抽象，比如在上面的例子中，我们将每一个特征，输入到一个神经元，这些接受输入的神经元构成了第一层神经网络，也叫做输入层，我们的目标是判断一个人的性别，是男是女分属于两个不同类别，我们将其抽象为一个神经元，这个神经元构成神经网络的输出层，每一个特征（输入层神经元），都有到分类（输出层神经元）的连接，也就是从特征转化为分类的概率（权重），通过综合各个连接的权重，传送到输出神经元。

 以上便是神经网络算法最简单的模型，神经网络算法的学习过程中，首先随机初始化各层神经元之间的连接权重（上文中的可能性），然后输入样本进行预测，根据预测的误差，调整神经网络中的权重，完成这个过程之后，我们的神经网络就训练好了。所以，神经网络训练的结果，就是得到各个连接的权重（经验），这样，一旦有新的数据输入神经网络的时候，就能推测出其分类了。

神经网络算法实例

问题定义

还是用上面的预测性别的例子，现在将其数学化，假设在一群人中，我们只能获得每个人的三个特征：

     特征1：长发（1）还是短发（0）

     特征2：衣服颜色是红色（1）还是不是红色（0）

     特征3：身高大于178cm（1）还是不超过178（0）

假设我们只知道其中四个人的性别（男：0，女：1），我们需要依据这四个人的三个特征以及性别训练一个神经网络，用于预测一个人的性别。样本信息如下：

头发	衣服	身高	性别
0	0	1	0
1	1	1	1
1	0	1	1
0	1	1	0

下面我们先实现最简单的单层神经网络。我们用X表示输入的特征向量，由于每个样本有三个特征，一共有四个样本，所以我们定义一个4X3的矩阵，每一行代表一个样本，如下代码所示。其中，NumPy是Python语言的一个扩充程序库。支持高级大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。

而四个样本对应输出（分类结果）我们用一个1X4的矩阵表示。“.T”为转置函数，转置后变成了4X1的矩阵。同我们的输入一致，每一行是一个训练实例，而每一列（仅有一列）对应一个输出节点。因此，这个网络还有三个输入和一个输出。代码如下所示：

训练开始之前，我们先要初始化神经网络的权重，由于输入层有三个神经元，而输出结果只有一个神经元，所以权重矩阵为3X1。由于一般初始化权重是随机选择的，因此要为随机数设定产生的种子，如下第一行代码所示。这样可以使每次训练开始时，得到的训练随机数都是一致的。这样便于观察策略变动是如何影响网络训练的，消除初始权重的影响。
　

对于第二行代码，这里由于我们要将随机初始化的权重矩阵均值设定为 0 （至于权重矩阵的初始化，大家有兴趣的话，请查看相关资料）。因此使用第二行代码来计算syn0(第一层网络间的权重矩阵)，如下所示：

为了将输出的权重归一化，定义一个sigmoid函数，其定义为：

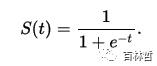
sigmoid函数可以用以下Python代码实现，其中，deriv参数表示是否计算的是其导数值：

其函数图像如下图所示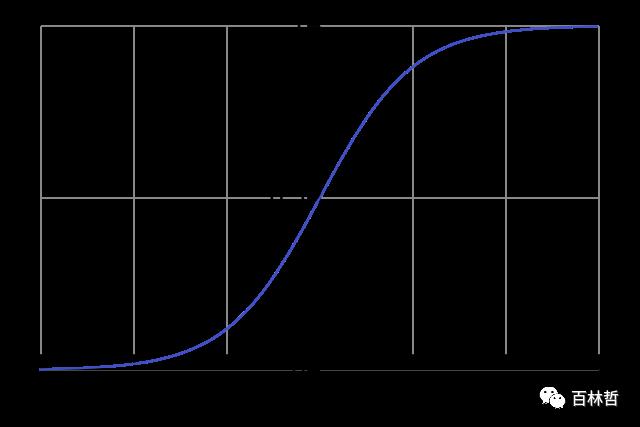：sigmoid函数的特点是，其导数可以用其自身表示出来，在计算的时候，我们只需要计算出其函数值，就可以计算出其导数值，从而可以减少浮点运算次数，提高效率，其导数如下：

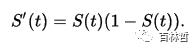
接下来，我们开始训练神经网络：

我们的训练过程迭代10000次，以得到一个较优的结果，每一次迭代的过程可以描述为：

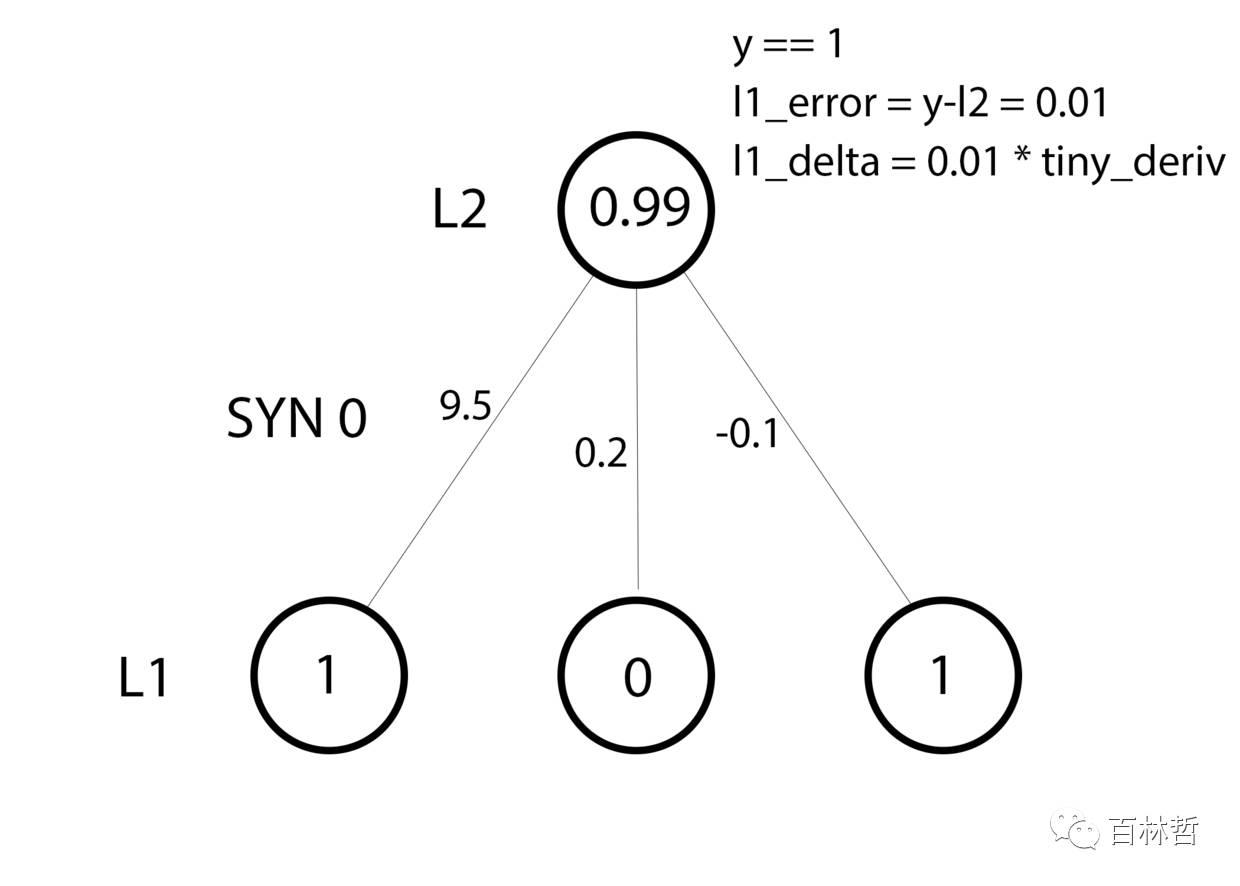
1、计算输入层的加权和，即用输入矩阵L0乘以权重矩阵syn0，并通

过sigmid函数进行归一化。得到输出结果l1；

2、计算输出结果L1与真实结果y之间的误差L1_error；

3、计算权重矩阵的修正L1_delta，即用误差乘以sigmoid

4、用L1_delta更新权重矩阵syn0

此处着重解释 下第三步，这里利用的是梯度下降法，算法的原理我们暂不深究，只需要明白其目的是为了使迭代后的误差逐渐减小即可。

一次训练过程的参数更新如下图所示：

由于我们的输入X中一共有四个样本，我们进行“批量的训练”，所以其过程类似于下图所示：

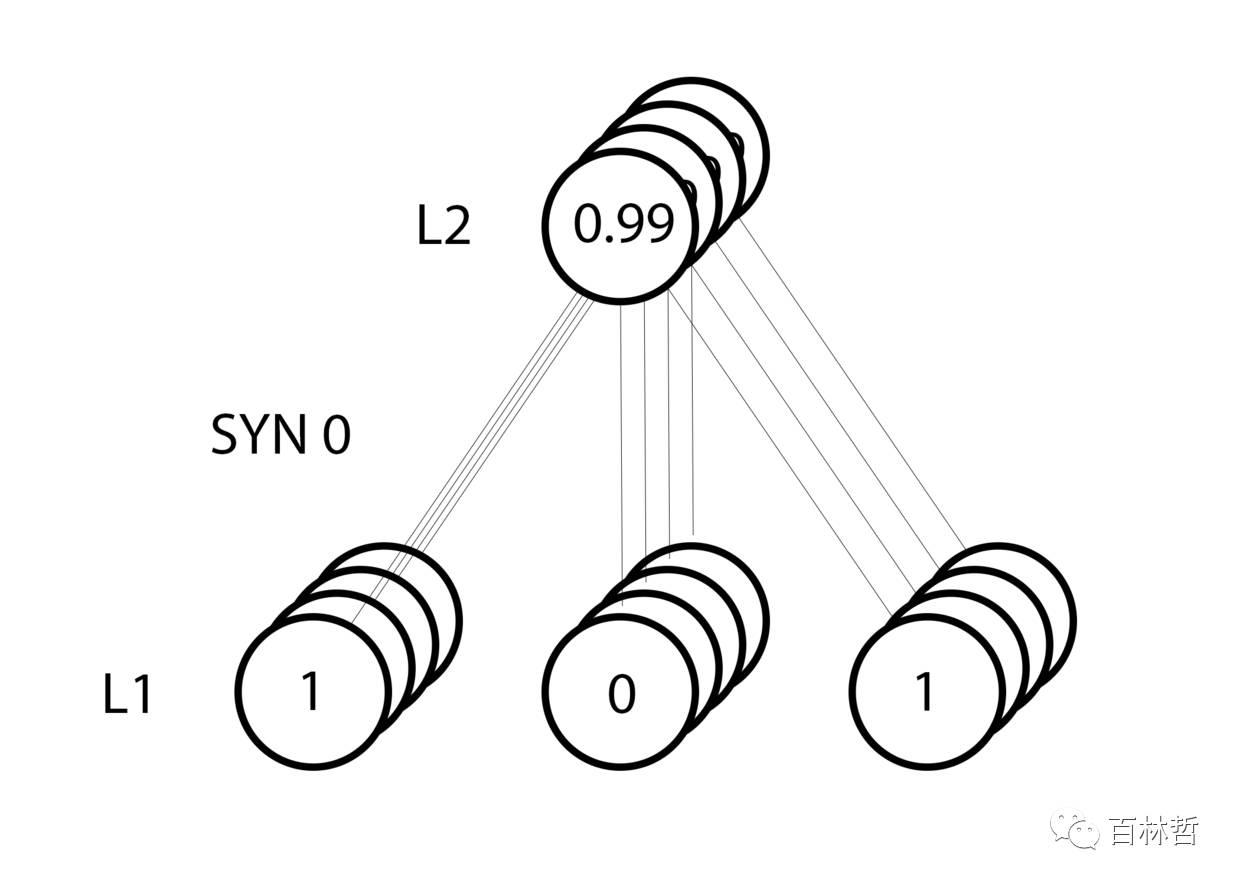
在上述代码中，我们通过10000次迭代，我们得到的输出结果如下：

可以看出，syn0的第一个元素，也就是第一个输入特征（长发）的权重最大，而第二个和第三个特征都很小，所以神经网络学习的结果是加重第一个特征的权重，而其他两个特征对于是女性这个推测的贡献较小，所以减小其权重。为了验证训练结果，我们加入两组新数据，(短头发，红衣服，矮个子)，(长头发，不是红衣服，矮个子)，并用神经网络来进行分类：

计算结果如下：

二层神经网络

上面的例子中，我们只用了一层神经网络，这只能解决线性问题，而现实中，一个孤立的特征并不是对应一个分类，还是用上面的例子说明：上面的问题中，我们假定了长头发是女性的概率一定大于男性，高个子是男性的概率一定大于女性，这种假设中，特征和分类是一种确定的关系，而特征之间没有依赖关系。而现在，我修改这种假设，在穿红衣服的人群中，长头发更可能是女性，而在穿其他颜色的衣服中，短头发更有可能是女性，此时，我们上面的神经网络模型就失效了，因为我们无法直接建头发这个输入特征到性别这个输入的直接联系。
　　

为了解决上面的问题，我们需要在加入一层神经网络，将输入层的特征进行组合，然后在传导到输出层，这就是二层神经网络的模型，其示意图如下：

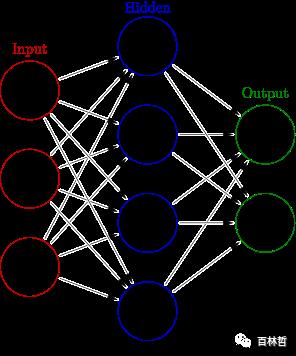
中间加入的这一层佳作隐含层，由于这一层的加入，我们多了一层传导，所以初始化的时候需要再加入一个权重矩阵：

两层神经网络的学习更新过程如下：

结合前面的单层神经网络的实现，就很容易理解上面的代码了，代码中，L0的输出没有直接作为最终输出层，而是传导给了L2层，L2层以相同的方式传导到输出层。而更新权重的时候，采用的是相反的过程，先依据L2输出的误差，更新syn1，再用L2的误差乘以syn1，作为L1层的误差，最后用同样的方法更新第一层权重矩阵syn0

结语

这篇文章以最简单的方式构建了一个基本的神经网络，虽然离实用还相去甚远，但是已经初现神经网络的雏形框架，如果需要构建一个实用级别的神经网络，还需要加入一些其他的功能，原作者建议我们从以下这些概念开始入手，优化我们的神经络）：

• Alpha

• Bias Units

• Mini-Batches

• Delta Trimming

• Parameterized Layer Sizes

• Regularization

• Dropout

• Momentum

• Batch Normalization

• GPU Compatability

• 其他脑洞