线性排序:桶排序计数排序
Posted 编程加油站
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性排序:桶排序计数排序相关的知识,希望对你有一定的参考价值。
一、桶排序

// 思路:
// 将数组中的数据,按桶进行划分,将相邻的数据划分在同一个桶中
// 每个桶用插入排序算法(或者快速排序)进行排序
// 最后整合每个桶中的数据
function bucketSort(array, bucketSize = 5) {
if (array.length < 2) {
return array
}
const buckets = createBuckets(array, bucketSize)
return sortBuckets(buckets)
}
function createBuckets(array, bucketSize) {
let minValue = array[0]
let maxValue = array[0]
// 遍历数组,找到数组最小值与数组最大值
for (let i = 1; i < array.length; i++) {
if (array[i] < minValue) {
minValue = array[i]
} else if (array[i] > maxValue) {
maxValue = array[i]
}
}
// 根据最小值、最大值、桶的大小,计算得到桶的个数
const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1
// 建立一个二维数组,将桶放入buckets中
const buckets = []
for (let i = 0; i < bucketCount; i++) {
buckets[i] = []
}
// 计算每一个值应该放在哪一个桶中
for (let i = 0; i < array.length; i++) {
const bucketIndex = Math.floor((array[i] - minValue) / bucketSize)
buckets[bucketIndex].push(array[i])
}
return buckets
}
function sortBuckets(buckets) {
const sortedArray = []
for (let i = 0; i < buckets.length; i++) {
if (buckets[i] != null) {
insertionSort(buckets[i])
sortedArray.push(...buckets[i])
}
}
return sortedArray
}
// 插入排序
function insertionSort(array) {
const { length } = array
if (length <= 1) return
for (let i = 1; i < length; i++) {
let value = array[i]
let j = i - 1
while (j >= 0) {
if (array[j] > value) {
array[j + 1] = array[j] // 移动
j--
} else {
break
}
}
array[j + 1] = value // 插入数据
}
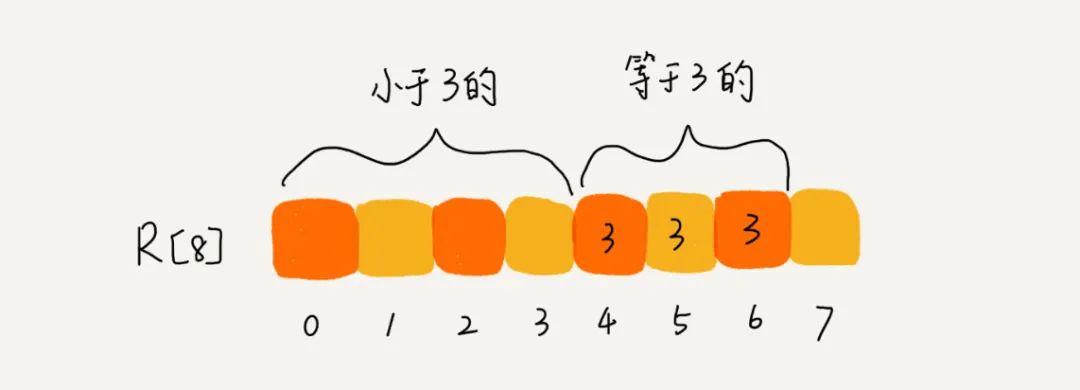
}二、计数排序
const countingSort = array => {
if (array.length <= 1) return
const max = findMaxValue(array)
const counts = new Array(max + 1)
// 计算每个元素的个数,放入到counts桶中
// counts下标是元素,值是元素个数
array.forEach(element => {
if (!counts[element]) {
counts[element] = 0
}
counts[element]++
})
// counts下标是元素,值是元素个数
// 例如:array: [6, 4, 3, 1], counts: [empty, 1, empty, 1, 1, empty, 1]
// i是元素, count是元素个数
let sortedIndex = 0
counts.forEach((count, i) => {
while (count > 0) {
array[sortedIndex] = i
sortedIndex++
count--
}
})
return array
}
function findMaxValue(array) {
let max = array[0]
for (let i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i]
}
}
return max
}
console.log(countingSort([7, 5, 1, 9, 2, 3, 6]))以上是关于线性排序:桶排序计数排序的主要内容,如果未能解决你的问题,请参考以下文章