排序4-归并排序与快速排序

Posted 2021-05-02 嵌入式Max

隔了一周，整的差不多了，在学习的过程中会发现不管是什么样的数据结构或者是算法，最重要是要掌握其思想，还有少量核心的编程技巧，其它大部分都是边边角角的，这两个是核心，所谓要知其然，更要知其所以然，这样才能够应付众多的数据结构，否则每一个都要靠硬记是很伤神的。

还有一个就是别人的代码不管写的再怎么简洁了，看起来还是比较难以理解，所以掌握思想才是最重要的，就好像同一个意思你的表达跟别人的表达是不一样的，学别人的表达方式是很难的，但是掌握实现表达目的的方式，用自己的语言来描述就很清晰。

分治与递归

「分治」是一种解决问题的思想，这个我是十分理解的，因为工作中接触到的很多很多问题，负责的几个专题都是需要用到「分治」这一思想的，扯点别的，工作一段时间你会发现问题的分解是一个很重要的技能，因为有些东西直接给你做你初看下来是不知道该如何下手的，只有把整个问题拆解下来才能够有序解决。

之前的时候通常接手的都是已经分解好的子问题，觉得分配问题的工作好轻松啊，就是把问题分解下，然后分发给相关人员解决嘛。等到自己去做的时候发现问题的分解也是个很难的事情，有些问题你都不知道该怎么去分解，该采用什么方案分解，分解下来的子问题是不是合理也是个难点。算了，说回分治，总之它就是一个把大问题拆解成小问题的这么「简单」的一个思想。

「递归」是一种编程的技巧，有关分治解决子问题的执行过程可以采用递归来完成，递归在某种程度上来讲很适合去解决一些需要用到分治思想的问题，其主要特点是：

1. 一个大的问题可以拆解成若干个小的问题。

2. 每一个子问题的解决方式都是一样的，或者说是非常类似的。

3. 左右的子问题归总到最后会有一个终止条件。

只要满足上述的条件都可以采用「分治」➕「递归」的方式去解决，递归的编程方式如果要深入到细节里面去的话是比较难以理解的，因为人脑思考不适合这种层峦叠嶂的过程展开，我们还是更适合直来直去的思维方式，关于递归，大多数学霸讲的是：

1. 不要过度关注递归的展开。

2. 抓住递归的子问题这个小范围的问题解决，然后找到递推公式。

3. 找好终止条件。

本文涉及到的两种排序算法都是需要用到这两个概念的，所以这里就先简单的提一下。

合并

这个是合并的动作，会有很多优化的归并排序用到这些代码，这些都是我根据自己的理解写出来的，肯定不是最优的代码，但是自己思考的过程得出的结果还是很有用的，这里就先贴出来：

/* dst_butt 与 merge_butt 必须是等长的。 */
static void __merge(int *dst_butt, int *merge_butt, int left_idx, int mid_idx, int right_idx)
{
    int i = left_idx, j = mid_idx+1;
    int sort_tmp_cnt = i;

    j = j > right_idx ? right_idx : j;

    while (i <= mid_idx && j <= right_idx) {
        if (merge_butt[i] <= merge_butt[j])
            dst_butt[sort_tmp_cnt++] = merge_butt[i++];
        else
            dst_butt[sort_tmp_cnt++] = merge_butt[j++];
    }

    if (i > mid_idx) {
        for (i = j; i <= right_idx; i++)
            dst_butt[sort_tmp_cnt++] = merge_butt[i];
    } else {
        for (j = i; j <= mid_idx; j++)
            dst_butt[sort_tmp_cnt++] = merge_butt[j];
    }
}

「归并排序」

其主要的思想是把待排序的数组从整体拆解成最多包含两个元素的子排序单元，然后从下到上依次合并排序好的子排序单元，最终形成的数组就是有序的了，归并排序是可以做到稳定的，也就是相同元素在排序前后的相对顺序是不变的。

上面的图是从维基百科获取到的，自己懒得画，很费时间的，上面的动图已经可以很形象的去描述归并排序的排序过程了，可以看到它并不是一个原地的排序算法，需要有另外一个辅助数组来存放临时变量。

归并排序的英文名词是「merge sort」，按照通常的直译就是合并排序，我找了找为什么会翻译成归并的信息，但是没有收获，按照我的理解，在归并排序的实际操作过程当中是包含了递归与合并两个过程的，所以理解「归」就是递归的意思，「并」就是合并的意思，不一定是真实的含义。

贴下归并排序使用递归方式写的代码（看下它的结构是不是很符合先递归后合并的特征）：

static inline void __merge_sort(int *sort_butt, int *sort_tmp, int left_idx, int right_idx)
{
    int mid_idx = left_idx + (right_idx - left_idx) / 2;

    if (left_idx + 1 < right_idx) {
        __merge_sort(sort_butt, sort_tmp, left_idx, mid_idx);
        __merge_sort(sort_butt, sort_tmp, mid_idx+1, right_idx);
    }

    /* 上面有相关的 __merge 代码实现 */
    __merge(sort_tmp, sort_butt, left_idx, mid_idx, right_idx);

    int i = 0;
    for (i = left_idx; i <= right_idx; i++) {
        sort_butt[i] = sort_tmp[i];
    }
}

它的终止条件是：left_idx + 1 >= right_idx

它的递推公式是：

__merge_sort(sort_butt, sort_tmp, left_idx, mid_idx);
__merge_sort(sort_butt, sort_tmp, mid_idx+1, right_idx);

找到这两个元素，就可以很简单的写出归并排序的代码了，上面的代码还有优化的余地，就是不必每次合并的操作都要重复的两次拷贝数组数据，于是有下面的优化代码：

/* 需要提前拷贝原始数组数据到 tmp_butt 里面，保证它们完全一致 */
static inline void __perform_merge_sort(int *sort_butt, int *tmp_butt, int left_idx, int right_idx)
{
    int mid_idx = left_idx + (right_idx - left_idx) / 2;

    if (right_idx - left_idx > 1) {
        __merge_sort(tmp_butt, sort_butt, left_idx, mid_idx);
        __merge_sort(tmp_butt, sort_butt, mid_idx+1, right_idx);
    }

    __merge(sort_butt, tmp_butt, left_idx, mid_idx, right_idx);
}

看起来好像区别不太大，主要就是递推过程那个 tmp_butt 与 sort_butt 的位置有变化，这个优化采用了暂存数组与原始排序数组角色互换的方式，同一个层级的每两次归并操作之后就把两者的角色对调，这样就可以保证每次只有一次拷贝动作。

还有个问题是，怎么保证最后一次一定是把 tmp_butt 里面的数据给搬运到 sort_butt 里面？数据被切分之后总归是有奇有偶的，如何保证这一点？在上面的代码里面，__merge 函数的数组角色是与 __perform_merge_sort 的保持一致的，也就是说最后一个退出的递归操作一定是最顶层的 __merge 操作，最顶层的那个一定不会搞错原始数组与暂存数组的关系的。也就是说，最后一步合并操作永远都是从 tmp_butt 到 sort_butt。

这里面的细节问题我是无法展开去想象的，其实到这里我是懂为什么最后一步能够保证操作的正确性，但是为什么它这样就是可以的呢？不知道我有没有表达清楚我的疑问，就是「道理我都懂，但是这个鸽子它为什么这么大呢？」，这是我一直有的一个疑问，因为我没有理清楚中间过程，直到我写完了非递归模式下的归并排序代码实现。

根据测试，我实际发现两者的时间差距并不大，我觉得是因为优化之后的代码在最开始的时候有一个完整数组的拷贝动作（数组角色交换所必须的），但是优化之前的不需要拷贝，虽然理论上来讲小规模数据一次一次的拷贝是要比大规模数据一次性拷贝要快一点点的，但是实际上在我的机器上看来并不是这样的，只能说这个优化在我的机器上面是鸡肋的，在数据规模达到100万的时候才能看出稍微明显的时间差距。

非递归的「归并排序」

void non_recursive_merge_sort(int *sort_butt, int size)
{
    int *sort_tmp = malloc(size*sizeof(int));

    memcpy(sort_tmp, sort_butt, sizeof(int)*size);

    int gap = 1;
    int left_idx = 0, right_idx = 0, mid_idx = 0;
    bool exchange_flag = 0;
    bool exit_flag = 0;

    while (1) {
        left_idx = 0;
        right_idx = gap*2 - 1;
        mid_idx = left_idx + (right_idx - left_idx) / 2;

        if (right_idx >= size - 1)
            exit_flag = 1;
        right_idx = right_idx >= size ? size - 1 : right_idx;

        if (!exchange_flag) {
            while (mid_idx < size-1) {
                __merge(sort_butt, sort_tmp, left_idx, mid_idx, right_idx);
                left_idx += gap*2;
                right_idx = left_idx + gap*2 - 1;
                mid_idx = left_idx + (right_idx - left_idx) / 2;
                right_idx = right_idx >= size ? size - 1 : right_idx;
            }
            if (left_idx < size)
                memcpy(&sort_butt[left_idx], &sort_tmp[left_idx], sizeof(sort_butt[0])*(size-left_idx));
        } else {
            while (mid_idx < size-1) {
                __merge(sort_tmp, sort_butt, left_idx, mid_idx, right_idx);
                left_idx += gap*2;
                right_idx = left_idx + gap*2 - 1;
                mid_idx = left_idx + (right_idx - left_idx) / 2;
                right_idx = right_idx >= size ? size - 1 : right_idx;
            }
            if (left_idx < size)
                memcpy(&sort_tmp[left_idx], &sort_butt[left_idx], sizeof(sort_tmp[0])*(size-left_idx));
        }

        exchange_flag = !exchange_flag;

        gap *= 2;

        if (exit_flag)
            break;
    }

    if (exchange_flag) {
        printf("Bingo, that is good.\n");
    } else {
        printf("Bad news, should do more copy.\n");
        memcpy(sort_butt, sort_tmp, sizeof(int)*size);
    }

    free(sort_tmp);
}

代码是按照我自己的理解来写的，所以看起来比较难懂也是正常的，这是因为我写的太乱了，用图片来描述上面的代码就是：

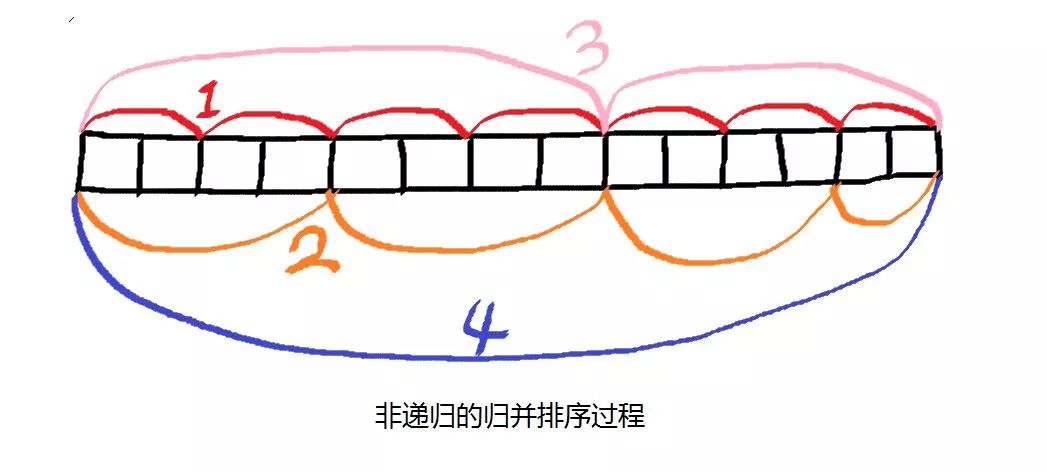
上面的代码保留了暂存数组与原始数组角色互换的操作，是用一个标记位来实现的，每个层级的归并完成之后就交换角色，最后还会判断退出时候角色的位置，如果不幸的话还会多一次拷贝操作，我想之前的递归形式代码只不过把这一步隐藏到了递归的过程中而已。

「快速排序」

它与归并排序是十分类似的最本质的区别有这么几个：

1. 它不是稳定的排序算法，相同值的两个元素在排序前后的相对位置可能会发生变化。

2. 区别于归并排序，它是自顶向下的排序算法，也就是先整体后局部。

3. 它是原地的排序算法，不需要再额外去申请更多的内存空间。

其基本的思想是：对于一个分割好的排序区间，找到一个分割值，然后把大于其的数据放到排序序列的最右边，把小于其的数据放到排序序列的最左边，然后不断地缩小排序区间，直到数据变得有序。

下面一幅图就是对整个排序序列分割的过程，可以很明显的看到自顶向下的过程，先对整个数组进行基于分割值的分割操作，然后再是余下的子序列分割操作：

void __quick_sort_recursive(int *sort_butt, int left, int right)
{
    int i = left, j = right;
    int pivot_idx = pick_pivot(sort_butt, left, right);
    int pivot_tmp = sort_butt[pivot_idx];
    int swap_tmp = 0;

    swap_tmp = sort_butt[left];
    sort_butt[left] = sort_butt[pivot_idx];
    sort_butt[pivot_idx] = swap_tmp;
    pivot_idx = 0;

    if (left < right) {
        //sort
        while (i < j) {
            while (j > i && sort_butt[j] >= pivot_tmp) j--;
            while (j > i && sort_butt[i] <= pivot_tmp) i++;

            swap_tmp = sort_butt[i];
            sort_butt[i] = sort_butt[j];
            sort_butt[j] = swap_tmp;
        }
        sort_butt[left] = sort_butt[i];
        sort_butt[i] = pivot_tmp;

        //sort left
        __quick_sort_recursive(sort_butt, left, i-1);
        //sort right
        __quick_sort_recursive(sort_butt, i+1, right);
    }
}

上面的代码是基于递归的，首先选择当前排序区间的区分点，可以有很多种方案，我这里用 pick_pivot 来代替了，然后交换区分点和当前排序区间的第一个数据项，这一步是把其变成普通的快排模式，然后是实际的交换操作了。

有几个比较关键的点：

1. 区分点的选择，以及选择完毕之后要把它挪到当前排序区间的第一个。

2. 终止条件为 left >= right，此时代表当前排序区间里面只有一个以下的元素了。

3. 排序时采用两个哨兵的模式，其中右侧哨兵需要先行动。

4. 当前一轮排序结束要交换区分点与哨兵碰头的位置的数据。

5. 然后递归执行当前区分点两侧的排序区间进行排序。

其中为什么要右侧哨兵先动？这是因为左侧哨兵停留的位置永远是小于等于区分点的，右侧哨兵停留的位置永远是大于等于区分点的，想象一下结束标志，是两个哨兵碰头就算结束，最后还要交换区分点与碰头点，那我们就必须要保证碰头点的数据是小于等于区分点的，否则最后一步交换会把之前排好的序给打乱掉。如果想让左侧哨兵先动，那么在最初的区分点交换的时候应该交换到当前排序区间的最右侧。

非递归「快速排序」

快速排序的代码很好理解，前提是理解了快速排序的思想，掌握其思想之后写代码是很轻松的事情。快速排序也可以写成非递归的形式，我按照自己的理解写出来的代码如下：

void nonrecursive_quick_sort(int *sort_butt, int size)
{
    int *strack_butt = malloc(sizeof(int)*size);
    int strack_cnt = 0;

    int left = 0, right = size-1;

loop:
    while (left < right) {
        int i = left, j = right;
        int pivot_idx = pick_pivot(sort_butt, left, right);
        int pivot_tmp = sort_butt[pivot_idx];
        int swap_tmp = 0;

        swap_tmp = sort_butt[left];
        sort_butt[left] = sort_butt[pivot_idx];
        sort_butt[pivot_idx] = swap_tmp;
        pivot_idx = 0;

        //sort
        while (i < j) {
            while (j > i && sort_butt[j] >= pivot_tmp) j--;
            while (j > i && sort_butt[i] <= pivot_tmp) i++;

            swap_tmp = sort_butt[i];
            sort_butt[i] = sort_butt[j];
            sort_butt[j] = swap_tmp;
        }
        sort_butt[left] = sort_butt[i];
        sort_butt[i] = pivot_tmp;

        /* 把区分点右侧排序区间端点值入栈。 */
        strack_butt[strack_cnt++] = i+1;
        strack_butt[strack_cnt++] = right;

        left = left;
        right = i;
    }

    if (strack_cnt) {
        right = strack_butt[--strack_cnt];
        left   = strack_butt[--strack_cnt];
        goto loop;
    }

    free(strack_butt);
}

看起来也不是很麻烦，其思路是这样的，我先对当前的排序区间进行快排，然后把区分点后面的排序区间端点值放在一个数组栈里面存储，再继续排左侧的，直到满足退出条件。退出之后判断数组栈是否为空，如果不为空那就取出两个数，分别赋值给右端点与左端点（取决于你存入的顺序），然后回到之前的循环里面去，直到栈为空为止。

其实跟其他的实现思路差不多完全一致，我这里没有用可变长的栈来实现，只是用数组来简单的模拟了一个定长的栈，理论上来讲这个栈的长度为 N 就肯定够用了。中间的哨兵排序代码与之前的完全一致，只是多了入栈出栈的操作而已。

根据我的实际测试，在数据量为百万级别的时候非递归比递归的快一点点，千万级别就没啥区别了，唯一有区别的也就是栈的使用量了，手动模拟的栈实际存在于堆上，函数调用栈就真的是在栈区。

其余的优化还有聚集与区分点相同元素到区分点周围，采用更加科学的方式选择区分点（根据我的测试，对于随机数来说，三数取中法与去当前排序区间中间值效果是差不多的），使用尾递归优化等等我就没再去深究了，毕竟排序思想才是最重要的。

End

这两种排序的时间复杂度平均都是 O(N*logN)，其中归并排序的空间复杂度是O(N)，而快速排序是O(1)，惯例，做一个对比测试。

算法	数组长度	时间消耗/ms
经典冒泡	10000	453
优化冒泡	10000	297
鸡尾酒	10000	250
梳排序	10000	2
插入排序	10000	109
优化的排序	10000	81
二分查找优化的插入排序	10000	62
希尔排序	10000	2
选择排序	10000	146
优化的选择排序	10000	87
递归归并排序	10000	1.52
非递归归并排序	10000	1.29
递归的快排	10000	1.38
非递归的快排	10000	1.33

下周清明节放假，就不更新算法相关的内容了，可能会不定期的更新点游记啊，思考啊啥的，清明时节雨纷纷，适合凭吊逝者以及吃东西，准备长沙走一波了。

阅读原文获取：代码链接-Newbie-C

---

想做的事情就去做吧