搜索与排序—— 归并排序与快速排序

Posted 2021-05-02 鲸骑

搜索与排序（四）—— 归并排序与快速排序

本节我们来学习一下排序中效率较高的两种。

归并排序

归并排序采用分而治之策略来提高算法性能。实现原理是采用递归，不断将列表拆分成一半，直至列表为空或只有一个项，再按基本情况进行排序；一旦两半排序完成，执行合并的基本操作。

图解

一、拆分

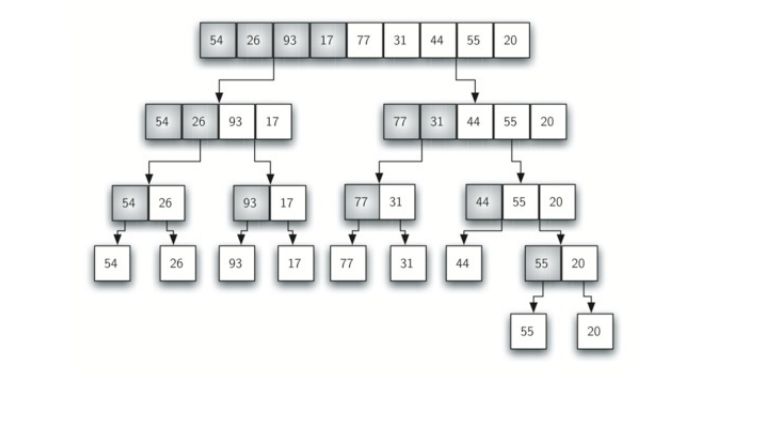
二、排序与合并

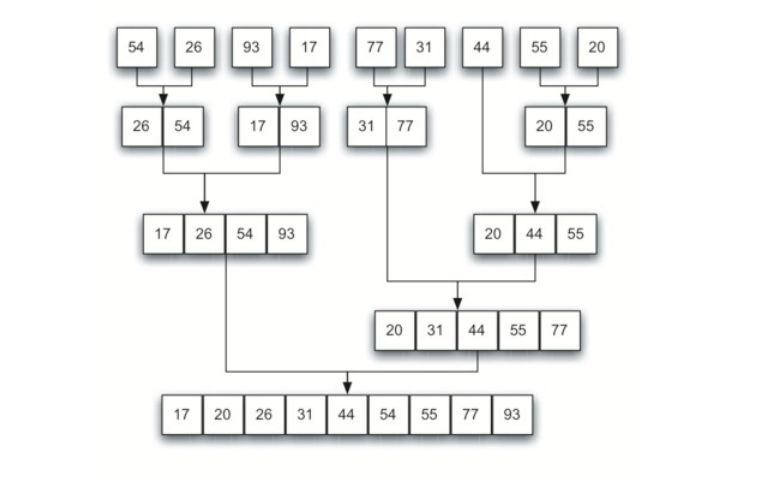
代码

 1def mergeSort(alist):
 2    if len(alist) > 1:
 3        mid = len(alist) // 2
 4
 5        lefthalf = alist[:mid]
 6        righthalf = alist[mid:]
 7
 8        mergeSort(lefthalf)
 9        mergeSort(righthalf)
10
11        i, j, k = 0, 0, 0
12
13        while i < len(lefthalf) and j < len(righthalf):
14            if lefthalf[i] <= righthalf[j]:
15                alist[k] = lefthalf[i]
16                i += 1
17            else:
18                alist[k] = righthalf[j]
19                j += 1
20            k += 1
21
22        while i < len(lefthalf):
23            alist[k] = lefthalf[i]
24            i += 1
25            k += 1
26
27        while j < len(righthalf):
28            alist[k] = righthalf[j]
29            j += 1
30            k += 1

复杂度

将列表递归划分需要log^n次，每次排序合并需要进行n个操作。故总复杂度为O(nlog^n)。
不过需要注意的是，归并算法在递归中需要额外的空间来保存两个半部分。如果列表很大，空间占用会非常大。

快速排序

快速排序也采用了分而治之来提高效率，而且与归并算法相比，不需要额外的空间来存储。

实现原理是先选择一个枢纽值（本文选择枢纽值的较简单，采用列表首个元素为枢纽值），在从左（列表第二项）往右选择一个比枢纽值大的元素作为左标记，从右（列表末尾项）往左选择一个比枢纽值小的元素为右标记。接着交换左右标记的值。在重复寻找左右标记，直至右标记的位序小于左标记，此时交换枢纽值与右标记。

然后以交换后的枢纽值位置划分列表位两部分，对每一部分进行上诉同样的操作。

图解

一、第一轮交换

该图演示了第一轮中的全部交换过程。

二、分割列表继续局部交换。

代码

 1def quickSort(alist):
 2    quickSortHelper(alist, 0, len(alist)-1)
 3
 4
 5def quickSortHelper(alist, first, last):
 6    if first < last:
 7        splitpoint = partition(alist, first, last)
 8
 9        quickSortHelper(alist, first, splitpoint-1)
10        quickSortHelper(alist, splitpoint+1, last)
11
12def partition(alist, first, last):
13
14    leftmark = first + 1
15    rightmark = last
16
17    done = False
18
19    while not done:
20
21        while alist[leftmark] <= alist[first] and leftmark <= rightmark:
22            leftmark += 1
23
24        while alist[rightmark] >= alist[first] and rightmark >= leftmark:
25            rightmark -= 1
26
27        if rightmark < leftmark:
28            done = True
29        else:
30            alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
31
32    alist[first], alist[rightmark] = alist[rightmark], alist[first]    
33
34    return rightmark

复杂度

如果交换后的枢纽值总是出现在列表中部左右，则每轮划分操作需要log^n, 每轮比较交换需要n, 复杂度位O(nlog^n)。

不过需要注意的是，交换后的枢纽值如果一直在列表左右侧的话，最坏的情况下降到递归划分需要O(n)了，总为O(n^2)。

所有枢纽值的选择很关键。有一种选择枢纽值的算法是比较列表的首项，末尾项，以及中间项三项中的中间大小值作为枢纽值。有兴趣的朋友可以自行尝试一下。

- end -