快速排序-插入排序-归并排序

Posted 2021-04-25 小秋的博客

快速排序算法

快速排序的思想

代码实现

 
   
   
 

  
    
    
  
import java.util.Arrays;
  
    
    
  


  
    
    
  
public class QuickSort {
  
    
    
  
 public static void main(String[] args){
  
    
    
  


  
    
    
  
 QuickSort quickSort = new QuickSort();
  
    
    
  
 int arr[] = {4, 6, 1, 2, 9, 0, 3, 11, 5};
  
    
    
  
 quickSort.quickSort(arr);
  
    
    
  
 System.out.println(Arrays.toString(arr));
  
    
    
  
 }
  
    
    
  


  
    
    
  
 public void quickSort(int[] arr){
  
    
    
  
 quickSortSub(arr,0,arr.length - 1);
  
    
    
  
 }
  
    
    
  
 public void quickSortSub(int[] arr,int low,int high){
  
    
    
  
 if(low < high){
  
    
    
  
 int middle = partition(arr, low, high);
  
    
    
  
 quickSortSub(arr, low, middle - 1);
  
    
    
  
 quickSortSub(arr,middle + 1,high);
  
    
    
  
 }
  
    
    
  
 }
  
    
    
  


  
    
    
  
 public int partition(int[] arr,int low,int high){
  
    
    
  
 int base = arr[high];
  
    
    
  
 int i = low - 1;
  
    
    
  
 for(int j = low; j <= high - 1; j++){
  
    
    
  
 if(arr[j] <= base){
  
    
    
  
 i++;
  
    
    
  
 swap(arr,i,j);
  
    
    
  
 }
  
    
    
  


  
    
    
  
 }
  
    
    
  
 swap(arr,i+1,high);
  
    
    
  
 return i + 1;
  
    
    
  
 }
  
    
    
  


  
    
    
  
 public void swap(int[] arr,int i,int j){
  
    
    
  
 int temp = 0;
  
    
    
  
 temp = arr[i];
  
    
    
  
 arr[i] = arr[j];
  
    
    
  
 arr[j] = temp;
  
    
    
  
 }
  
    
    
  


  
    
    
  
}
 
   
   
 

partition函数的另外一种实现方式

实现partition函数有很多种方式，前面介绍的方式是两个指针low和high都是从头开始，向同一个方向移动，high指针在low的前面，high指针标记的是比基准数大的，low指针标记的是比基准数小的

接下来我们同样采用两个指针low和high，只不过这两个指针是相向运动，当两个指针相遇的时候就停止

 
   
   
 

  
    
    
  
 public int partition1(int[] arr,int low,int high){
  
    
    
  
 int base = arr[low];
  
    
    
  
 int i = low;
  
    
    
  
 int j = high;
  
    
    
  
 while (i < j){
  
    
    
  
 while ( arr[j] > base) j--;
  
    
    
  
 if(arr[j] < base){
  
    
    
  
 swap(arr, i, j);
  
    
    
  
 i++;
  
    
    
  
 }
  
    
    
  
 while (arr[i] < base) i++;
  
    
    
  
 if(arr[i] > base){
  
    
    
  
 swap(arr,i,j);
  
    
    
  
 j--;
  
    
    
  
 }
  
    
    
  
 }
  
    
    
  
 return i;
  
    
    
  
 }
 
   
   
 

时间复杂度

• 最好时间复杂度

快速排序算法的时间复杂度关键在于拆分的时候是否平衡，如果每次拆分的时候，下标刚好在中间，即q = (p+r)/2

那么性能和归并排序一样都是O(nlogn)

• 最坏时间复杂度

如果拆分的时候，刚好拆分的地方另一部分只有一个元素，那么性能和插入排序没有什么区别，那么此时拆分需要拆分n次，对于每次拆分都需要调用partition函数找到拆分处的下标，partition的时间复杂度为θ(n)

所以最坏时间复杂度为：θ(n * n) = θ(n^2)

基于随机抽样的快速排序算法

时间复杂度

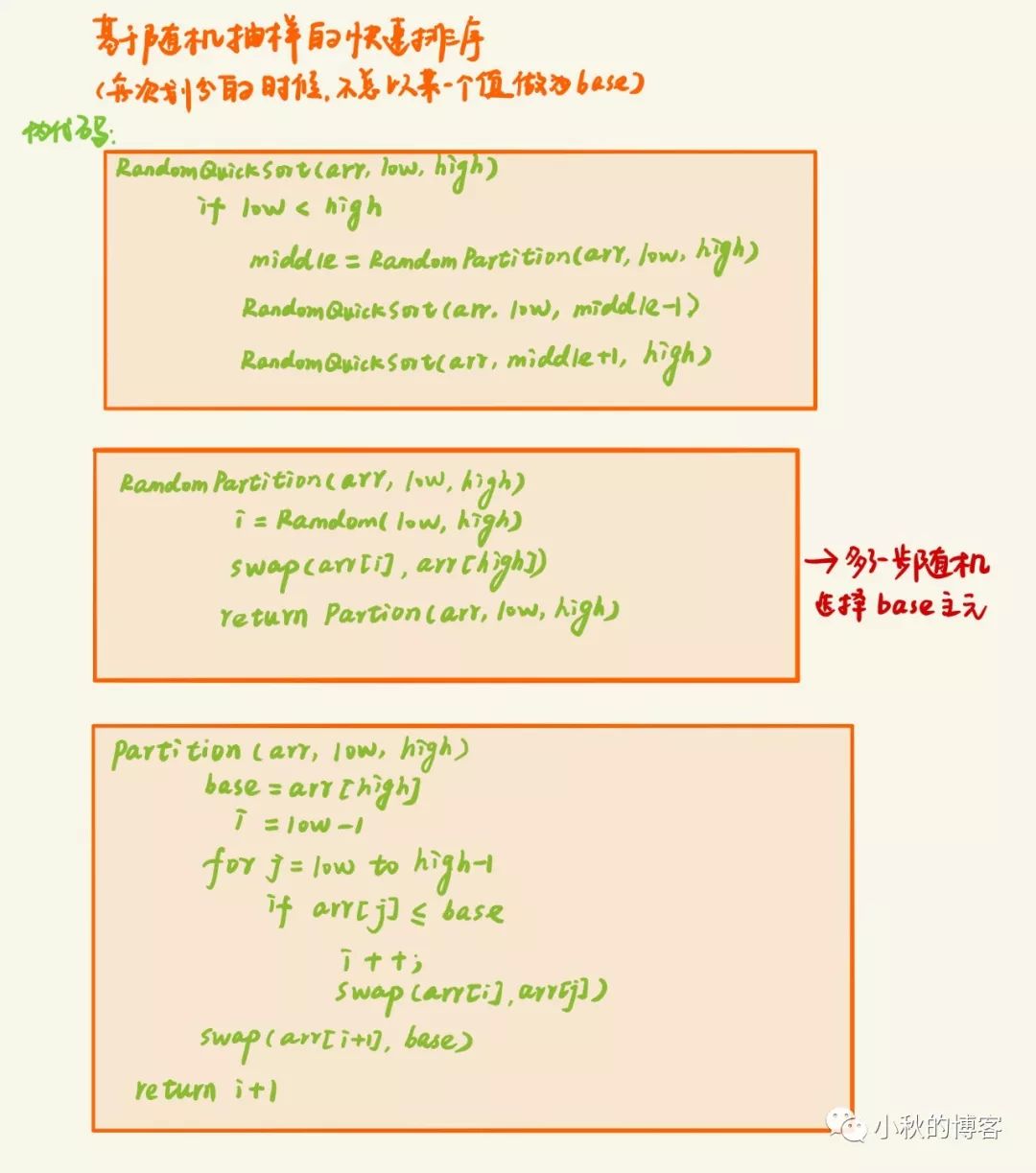
最坏时间复杂度：O(n^2)

平均时间复杂度：O(nlogn)（元素互异）

插入排序

插入排序的思想

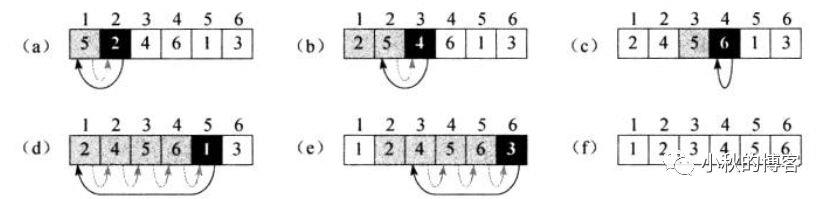
伪代码

实现

 
   
   
 

  
    
    
  
import java.util.Arrays;
  
    
    
  


  
    
    
  
public class InsertSort {
  
    
    
  
 public static void main(String[] args){
  
    
    
  


  
    
    
  
 InsertSort insertSort = new InsertSort();
  
    
    
  
 int[] arr = {3, 1, 2, 6, 5, 4};
  
    
    
  
 insertSort.insertSort(arr);
  
    
    
  
 System.out.println(Arrays.toString(arr));
  
    
    
  
 }
  
    
    
  


  
    
    
  
 public void insertSort(int[] arr){
  
    
    
  
 for(int i = 1; i < arr.length; i++){
  
    
    
  
 int key = arr[i];
  
    
    
  
 int j = i - 1;
  
    
    
  
 while (j >= 0 && arr[j] > key){
  
    
    
  
 arr[j + 1] = arr[j];
  
    
    
  
 j--;
  
    
    
  
 }
  
    
    
  
 arr[j + 1] = key;
  
    
    
  
 }
  
    
    
  


  
    
    
  
 }
  
    
    
  
}
 
   
   
 

时间复杂度：O(n^2)

归并排序算法

快速排序和归并排序都借助了分治的思想，但是他们也有所差别-

• 快速排序只有分的过程，而归并排序既有分的过程也有合的过程；

• 快速排序是在分的过程中通过partition函数找到每个子数组拆分的下标，直到子数组只有一个元素，这个时候就已经排好序了；而归并排序先通过平分的方法划分子数组，最后在合的过程进行排序

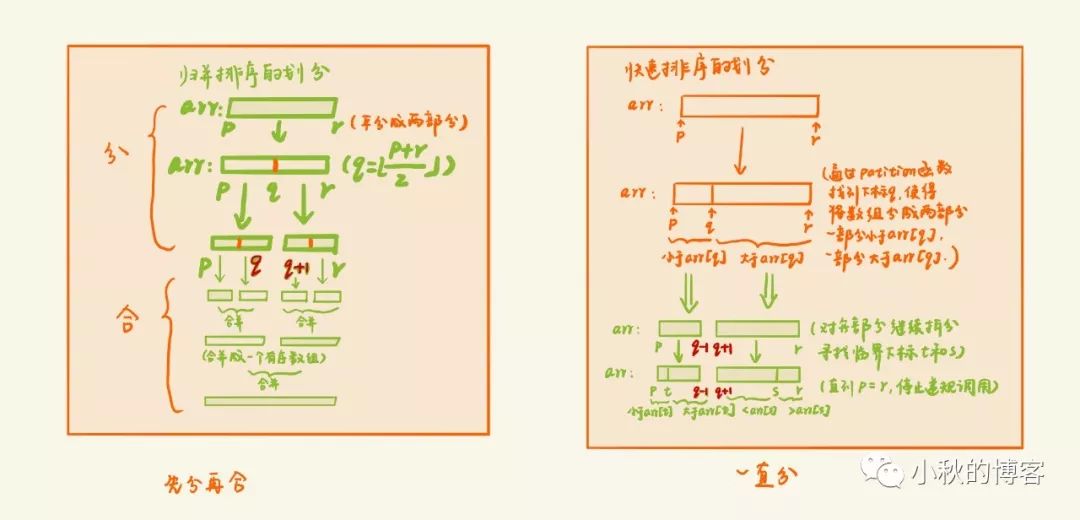
思想

实现

 
   
   
 

  
    
    
  
import jdk.nashorn.internal.objects.NativeInt16Array;
  
    
    
  


  
    
    
  
import java.util.Arrays;
  
    
    
  


  
    
    
  
public class MergeSort {
  
    
    
  


  
    
    
  
 public static void main(String[] args){
  
    
    
  


  
    
    
  
 MergeSort mergeSort = new MergeSort();
  
    
    
  
 int[] arr = {6, 2, 3, 9, 0, 1, 55};
  
    
    
  
 mergeSort.mergerSort(arr);
  
    
    
  
 System.out.println(Arrays.toString(arr));
  
    
    
  
 }
  
    
    
  
 public void mergerSort(int[] arr){
  
    
    
  
 mergeSortSub(arr,0,arr.length - 1);
  
    
    
  
 }
  
    
    
  
 public void mergeSortSub(int[] arr,int low,int high){
  
    
    
  
 if(low < high){
  
    
    
  
 int middle = (int) Math.floor((low + high) >> 1);
  
    
    
  
 mergeSortSub(arr,low,middle);
  
    
    
  
 mergeSortSub(arr,middle+1,high);
  
    
    
  
 merge(arr,low,middle,high);
  
    
    
  
 }
  
    
    
  
 }
  
    
    
  
 public void merge(int[] arr,int low,int middle,int high){
  
    
    
  
 int len1 = middle - low + 1;
  
    
    
  
 int len2 = high - middle;
  
    
    
  
 int[] arr1 = new int[len1 + 1 ];
  
    
    
  
 int[] arr2 = new int[len2 + 1];
  
    
    
  
 for(int i = 0; i < len1; i++){
  
    
    
  
 arr1[i] = arr[low + i];
  
    
    
  
 }
  
    
    
  
 for(int i = 0; i < len2; i++){
  
    
    
  
 arr2[i] = arr[middle + i + 1];
  
    
    
  
 }
  
    
    
  
 //防止数组越界
  
    
    
  
 arr1[len1] = Integer.MAX_VALUE;
  
    
    
  
 arr2[len2] = Integer.MAX_VALUE;
  
    
    
  
 int t = 0, s = 0;
  
    
    
  


  
    
    
  
 for(int i = low; i <= high; i++){
  
    
    
  
 if(arr1[t] <= arr2[s]){
  
    
    
  
 arr[i] = arr1[t];
  
    
    
  
 t++;
  
    
    
  
 }else {
  
    
    
  
 arr[i] = arr2[s];
  
    
    
  
 s++;
  
    
    
  
 }
  
    
    
  


  
    
    
  
 }
  
    
    
  


  
    
    
  
 }
  
    
    
  
}
 
   
   
 

时间复杂度

执行拆分的时候需要执行：log2(n)次

有多少次拆分就需要多少次合并，每次合并的时候需要比较的次数：n次，n = high - low + 1

所以总的时间复杂度为：θ(logn * n) = θ(nlogn)

参考

《算法导论》