时间序列分析：趋势时间序列分析之随机时间趋势

Posted 2021-05-02 SAS知识

上一篇文章介绍确定性时间趋势。今天，我们将介绍随机时间趋势。

随机时间趋势

另一种时间趋势是随机时间趋势，直观地讲，就是时间序列的趋势无法用一条单一的趋势线来刻画，在不同的时期，趋势线是变化漂移的，也就是说，趋势是随机的。对于这一类时间序列，其趋势线不能用时间的确定性函数来表示了，而是需要通过差分方式来描述。

对于非平稳时间序列，从理论上而言，足够多次的差分运算可以充分地提取原序列中的非平稳随机趋势。许多非平稳序列在进行差分运算后会显示出平稳时间序列的性质，因此，对于这类非平稳时间序列可以使用ARIMA模型进行拟合。

ARIMA模型可以表示为：

使用ARIMA过程进行随机趋势建模的基本语法为：

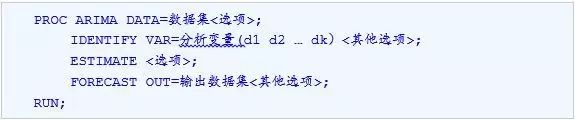
例如：

• “IDENTIFY VAR=VAR1（1）;” 表示对时间序列VAR1进行一阶差分，然后分析差分后新的时间序列。

• “IDENTIFY VAR=VAR1（1,1）;”表示对时间序列VAR1进行二阶差分，然后进行分析，分析的时间序列为

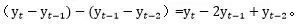
• “IDENTIFY VAR=VAR1（2）;”表示对时间序列VAR1进行两步差分，然后进行分析，分析的实际序列为

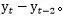
• 当ESTIMATE语句中不指定任何选项时，如

系统将只拟合均值MU，默认的模型为

该模型也称为带漂移项的随机游走模型。

因此，使用ARIMA过程进行非平稳序列建模的第一步就会要识别差分的阶数d，通过d阶差分将序列转换成平稳序列。一般情况下：

• 时间序列蕴含着显著的线性趋势，一阶差分就可以时间趋势平稳。

• 时间序列蕴含着曲线趋势，通常低阶（二阶）差分就可以提取出曲线趋势的影响。

• 对蕴含着固定周期的序列进行步长为周期长度的差分运算，通常可以较好地提取周期信息。

需要注意的是，差分运算的阶数并不是越多越好。因为差分运算是一种对信息提取、加工的工程，每次差分都会有信息的损失，所以在实际应用中，差分运算的阶数要适当，应当避免过度差分。

在ARIMA模型中，当d=1，p=q=0时，ARIMA（0,1,0）模型为：

该模型被称为随机游走（Random Walk）模型或者醉汉模型。作为一个最简单的ARIMA模型，随机游走模型是一个典型的含随机时间趋势的模型，目前广泛应用于计量经济学领域。传统的经济学家普遍认为投机价格的走势类似于随机游走模型，随机游走模型也是有效市场理论的核心。

另一个重要的ARIMA（0,1,0）模型是带漂移项的随机游走模型，模型表示为

来看图17.54中的两个序列，一个是趋势平稳时间序列，一个是带漂移项的随机游走序列，eps表示随机干扰。

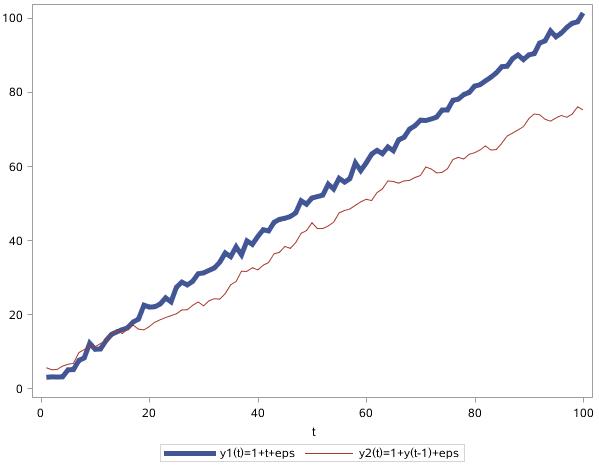
图17.54  趋势平稳时间序列和带漂移项

的随机游走序列

两个序列在图形上非常相似，似乎都包含线性趋势，很难区分。

但是，在实际应用中，如果凭借直观判断，错误地将带漂移项的随机游走当成趋势平稳过程，用趋势拟合法去除确定性趋势，并进行建模分析，那么由此而得出的结论是令人怀疑的。

因此，当我们遇到非平稳时间序列时，判断其包含的是确定性趋势还是随机趋势，对建模方法的选择有很大的影响。对于趋势平稳序列，可以用趋势拟合法消除确定性趋势；对于包含随机趋势的时间序列，则需要通过一阶差分将序列转化为平稳序列。

单位根检验

单位根检验（Unit Root Test）方法就是用来判断序列是否需要进行差分的方法，换言之，也就是用来判断序列是否平稳。在单位根检验法中，常用的是DF检验法。AR（1）过程可以表示为

由本章前面关于自回归模型的讨论可知，上式可以写成

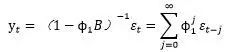
所以可以通过检验特征方程的根是在单位圆内（上）还是单位圆外，来检验序列的平稳性，这种检验就称为单位根检验。

由于现实生活中绝大多数序列都是非平稳序列，因此根据特征方程根的性质，将单位根检验的原假设和备择假设分别设定为：

DF检验可用于如下三种过程的平稳性检验：

第一种类型：无常数均值、无趋势的1阶自回归过程，这是我们之前一直分析的类型。

第二种类型：有常数均值、无趋势的1阶自回归过程，

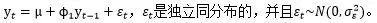
第三种类型：既有常数均值、又有线性趋势的1阶自回归过程，

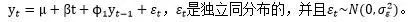
DF检验只适用于1阶自回归过程的平稳性检验，但是实际上绝大多数时间序列不会是一个简单的AR（1）过程。为了使DF检验能广泛地适用于AR（p）过程的平稳性检验，人们对DF检验进行了一定的修正，得到了增广DF检验（Augmented Dickey-Fuller），简记为ADF检验。DF检验是ADF检验的一个特例。

和DF检验一样，ADF检验也可以用于如下三种类型的平稳性检验。

第一种类型：无常数均值、无趋势的p阶自回归过程。

第二种类型：有常数均值、无趋势的p阶自回归过程。

第三种类型：既有常数均值、又有线性趋势的p阶自回归过程。

在ARIMA过程中，使用选项STATIONARY可以指定进行ADF检验，语法如下：

其中，当AR阶数为0时，表示进行上面介绍的三种类型（无常数均值、无趋势；有常数均值、无趋势；有常数均值和线性趋势）的1阶自回归过程平稳性检验；AR阶数为1时，表示进行上面介绍的三种类型的2阶自回归过程的平稳性检验；依此类推。可以同时指定进行多个阶数自回归过程的平稳性检验。

例17.10：数据集ex.production中的序列Prod代表一段时间内某种工业原料的市场供应量，试分析该序列是否平稳。

示例代码如下：

输出图17.55至图17.56所示（省略白噪声检验结果）。

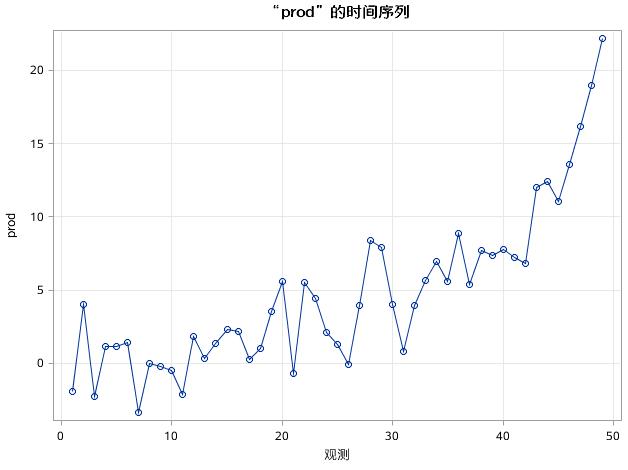
图17.55 例17.10中序列PROD的时序图

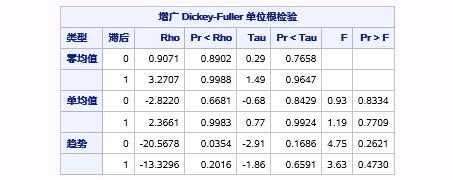
图17.56 例17.10中序列PROD的单位根检验报表

图中报表是序列Prod的时序图和ADF检验结果，类型一列的“零均值”、“单均值”和“趋势”分别对应着ADF检验的第一、二、三种类型。滞后一列有两种取值：0和1，分别对应着AR（1）过程和AR（2）过程。在SAS中，ARIMA过程的ADF检验，基于不同的方法分别构造了三种统计量Rho、Tau和F来进行单位根检验，并分别输出了三种统计量的取值和对应的P值。

一般情况下，三种统计量有如下参考准则：

• F统计量的检验不如Rho统计量和Tau统计量的检验结果准确，不太推荐参考。

• 当滞后为1（对应着AR（2）过程）时，Rho统计量的检验结果较Tau统计量更准确；其余情况下，Tau统计量的检验结果更具参考价值。

这里，结合时序图，我们看到序列带有一定的趋势，因此重点参考类型为“趋势”的单位根检验结果。根据上面介绍的参考准则，对于滞后为0和1两种情形下，p值都大于>0.05，说明不能拒绝原假设，即该序列是非平稳的。

本文结束，下一篇文章开始介绍运用ARIMA过程建立趋势模型。

回复【数据和代码】可以下载《深入解析SAS》一书的数据和代码。

查询往期文章，请回复下列关键字：

【安全】==>【SAS智能平台安全管理】系列文章

【Base基础】==>【Base SAS基础】系列文章

【编程概念】==>【SAS编程基本概念】系列文章

【描述性统计】==>【SAS统计分析系列：描述性统计分析】系列文章

【读外部数据】==>【读取外部数据到SAS数据集】系列文章

【假设检验】==>【参数估计与假设检验】系列文章

【单数据集处理】==>【单数据集处理】系列文章

【方差分析】==>【方差分析】系列文章

【主成分与因子分析】==>【主成分分析与因子分析】系列文章

【多数据集处理】==>【多数据集处理】系列文章

【判别分析】==>【判别分析】系列文章

【聚类分析】==>【聚类分析】系列文章

【线性回归】==>【线性回归】系列文章

【数据汇总展现】==>【数据汇总与展现】系列文章

【SQL语言】==>【SQL语言】系列文章

【LOGISTIC回归分析】==>【LOGISTIC回归分】系列文章

小贴士

读者可以从以下链接获取SAS公司提供的免费版环境：

SAS大学版（SAS® University Edition）是SAS为在校大学生免费提供的基于虚拟机和网页的SAS环境。回复关键字【大学版】，可以查看详细介绍。

下载路径：

https://www.sas.com/en_us/software/university-edition/download-software.html

SAS学术版（SAS® OnDemand for Academics）是 SAS 为学术届人士免费提供的、在线的、基于SAS 私有云上的应用服务环境。

用户首先需要注册，然后按照提示信息就可登录。

注册路径：

http://odamid.oda.sas.com

本文转自《深入解析SAS — 数据处理、分析优化与商业应用 》

如若转载本文，请在文章顶部标注 “本文转自SAS知识 （ID: SASAdvisor），摘自《深入解析SAS — 数据处理、分析优化与商业应用 》”

作者介绍

夏坤庄

《深入解析SAS — 数据处理、分析优化与商业应用》第一作者， SAS软件研究开发（北京）有限公司客户职能部总监。在承担研发工作的同时，夏及其团队负责对SAS非英语市场提供技术支持，并且与在美国及其它地区的团队一起，服务于SAS的SaaS/RaaS业务，同时提供和验证关于SAS产品和技术在应用领域的最佳实践。在加入SAS软件研究开发（北京）有限公司之前，夏就职于SAS中国公司，历任资深咨询顾问、项目经理、首席顾问、咨询经理，拥有丰富的咨询和项目实施经验。在长期的从业经历中，不但为SAS的金融行业客户成功实施了众多深受好评的项目，而且在近年领导实施了非金融行业的多个大数据分析项目。

SAS知识    微信：SASAdvisor     长按二维码关注

欢迎大家投稿，一起分享SAS的点滴

投稿邮箱:  [e-mail]