从HMM到RNN,机器学习中的时间序列模型

Posted 2021-05-02 JainMe

从HMM到RNN,机器学习中的序列模型（一）

时间：4月8日

分享人：Hachi

本次我们邀请了北师大系统学院的Hachi为大家分享他自己对机器学习中有关序列模型的认识。

简介

之前，我们分享的机器学习方法都是基于集合的分析方法，讨论的多个维度的数据的分类及聚类的方法。而序列，作为一种有着结构信息的数据，同样有着更深入挖掘的价值和相应的模型。

我们常见的序列有：文本、语音、股票数据等等。

主要内容

对于一个序列来说，比常见的点集，多了一个顺序关系，同时序列中的元素是可以重复的。我们可以这样定义一个序列：

设S是状态空间

${X(t)},t\in(0,inf),X(t)\inS$

称{X(t)}是S上的一个序列。

那么，我们好奇的是，给定一个序列，我想知道，序列的下个元素是啥？这个叫做预测。怎么去做预测呢？如果S是一个连续的空间，那么传统的方式有线性回归、灰度预测等等，如果S是一个离散的空间，简单一点的方法就是认为它是一个马氏过程，只对上一步的状态有记忆，对再前面的状态无记忆，那么可以得到它的状态转移方程，来做预测。那么，除了这些粗暴的方法，还有哪些方法呢？

在这次分享会里，我们介绍了：高阶的马尔可夫链模型，隐马尔科夫模型。

高阶马尔科夫链模型认为，下一时刻的状态，不仅仅与此时的状态有关，还与上一时刻，上上时刻有关，一般的，N阶马尔可夫链模型，认为下一时刻的状态与前N个状态有关。这样，最简单的，以二阶为例，我们可以通过参数估计得到P(vi->vj->vk)，其中Vi,Vj，Vk是状态空间的元素。得到一个比马尔可夫过程更好的对原始序列的描述。

而隐马尔可夫模型(HMM)，则认为，我们所看到的现实背后有着一套隐藏逻辑，以常见的筛子模型为例，

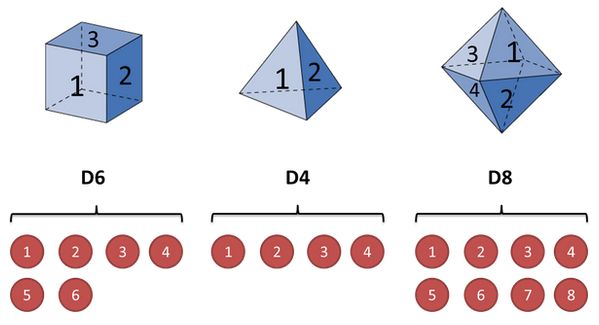
假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

那么，给我一个观测到的结果，我想知道下一次掷出结果是什么，那就要去问，下一个即将掷出的筛子是哪种筛子，于是，就去要知道每次更换换筛子的规律。

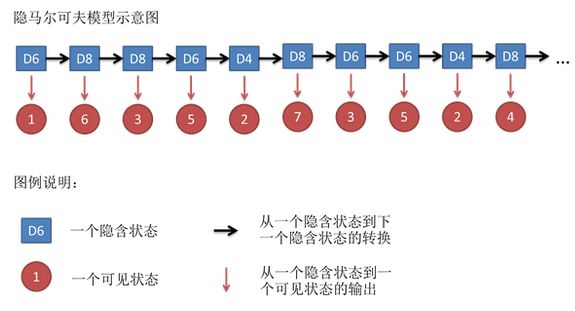
这个例子给出了经典的HMM想要解决的问题。这里的是筛子就是我的隐藏状态，每次掷出的结果就是我的观测值。（举一反三，如果我把人的声音信号序列看成输出值，那么隐藏状态是不是就可以认为是这段声音讯号对应的内容呢？这就是HMM最经典的一个应用，处理声音讯号。同样，HMM在分析DNA序列上也是一把好手）

通常，我们遇到的一个问题是知道隐含状态数量，转换概率矩阵，根据可见状态链，推测隐含状态链。这是经典的解码问题，可以利用维特比算法求解（基于动态规划）。具体过程见分享PPT，这里略过。

另一个我们常见的问题是，只给定一个观测序列和隐藏状态数，需要去求解状态转移矩阵A,观测概率矩阵B，以及初始状态$\lambda$，这是一个对隐变量估计的问题，我们可以用EM算法来求解。

分享人：Hachi

“这是我在JainMe的

 第 3 次分享”

下次活动预告：

从HMM到RNN,机器学习中的时间序列模型（二）

时间：4.14下午2：00

地点：北师大物理楼105

JainMe

和我一起遇见分享

长按二维码关注

点击“阅读原文”，获得分享内容