感谢中国人民大学的胡鹤老师,课程容量巨大,收获颇丰。
之前提到的CNN模型主要用到人类的视觉中枢,但其有一劣势,无论是人类的视觉神经还是听觉神经,所接受到的都是一个连续的序列,使用CNN相当于割裂了前后的联系。从而诞生了专门为处理序列的Recurrent Neural Network(RNN),每一个神经元除了当前信息的输入外,还有之前产生的记忆信息,保留序列依赖型。
一、RNN基本原理
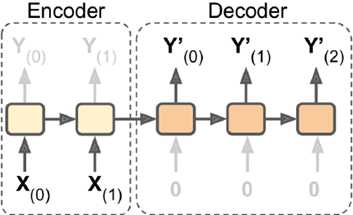
如下图所示有两种表示方法,每张图片左边是RNN的神经元(称为memory cell),右边是按时间轴展开后的情况。每次输入两个信息输出两个信息,每轮处理hidden state。把同样神经元在时间上展开处理,比CNN更加节省参数,是一个相当高效的表示方法。
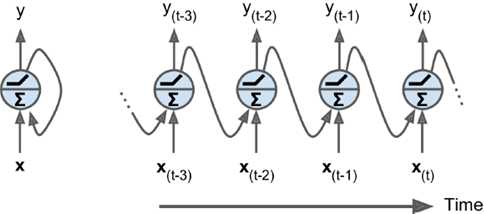
可参考如下公式表示,最后简化后的形式同一般神经元相同,输入信息乘权重加偏值:
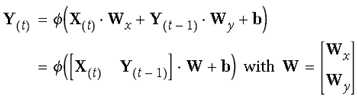
由于t状态的t由t-1时候决定,因而具有记忆功能,也叫作memory cell(或cell)
隐状态可由如下表示:
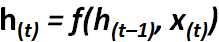
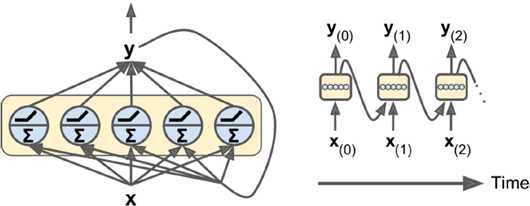
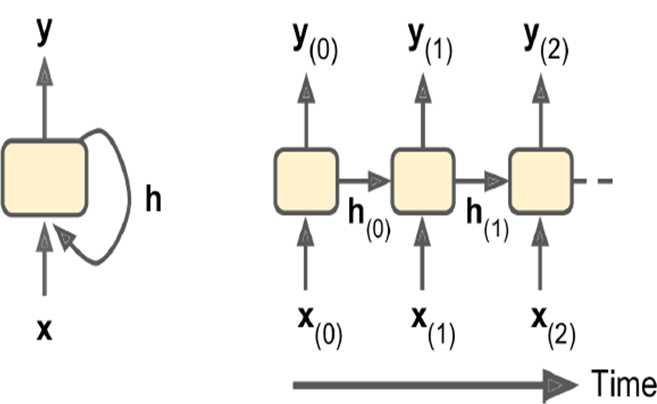
隐状态是当前t时刻的状态,也由t-1时刻决定,简单情况下,hidden state等同于output(y),但大多较为复杂的cell中,它们并不相同。如下图所示:
二、RNN种类:
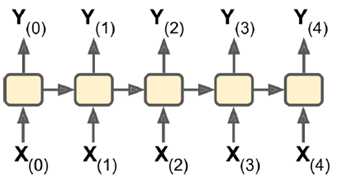
1. sequence-to-sequence:输入输出都是一个序列。例如股票预测中的RNN,输入是前N天价格,输出明天的股市价格。
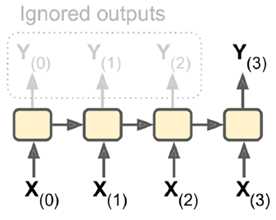
2. sequence-to-vector:输入是一个序列,输出单一向量。
例如,输入一个电影评价序列,输出一个分数表示情感趋势(喜欢还是讨厌)。
3. vector-to-sequence:输入单一向量,输出一个序列。
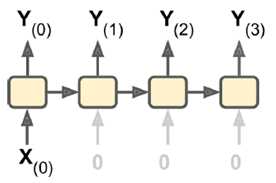
4.Encoder-Decoder:输入sequence-to-vector,称作encoder,输出vector-to-sequence,称作decoder。
这是一个delay模型,经过一段延迟,即把所有输入都读取后,在decoder中获取输入并输出一个序列。这个模型在机器翻译中使用较广泛,源语言输在入放入encoder,浓缩在状态信息中,生成目标语言时,可以生成一个不长度的目标语言序列。
三、RNN实例
1.手动实现
以下是一个手动实现RNN的实例
n_inputs = 3 # hidden state n_neurons = 5 X0 = tf.placeholder(tf.float32, [None, n_inputs]) X1 = tf.placeholder(tf.float32, [None, n_inputs]) # 由于Wx要和X相乘,故低维是n_inputs Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons],dtype=tf.float32)) # 低维,高维都是n_neurons,为了使得输出也是hidden state的深度 # 这样下一次才可以继续运算 Wy = tf.Variable(tf.random_normal(shape=[n_neurons,n_neurons],dtype=tf.float32)) b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32)) # Y0初始化为0,初始时没有记忆 Y0 = tf.tanh(tf.matmul(X0, Wx) + b) # 把上一轮输出Y0也作为输入 Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b)
init = tf.global_variables_initializer()
import numpy as np
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) # t = 0
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) # t = 1
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
# Y0,Y1都是4*5大小,4是mini-batch数目,5是输出神经元个数
TensorFlow函数集成后实现
2.static unrolling through time
static_rnn()是使用链式cells实现一个按时间轴展开的RNN
# 这种和上面那种手动实现的效果相同 n_inputs = 3 n_neurons = 5 X0 = tf.placeholder(tf.float32, [None, n_inputs]) X1 = tf.placeholder(tf.float32, [None, n_inputs]) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) output_seqs, states = tf.contrib.rnn.static_rnn(basic_cell, [X0, X1], dtype=tf.float32) Y0, Y1 = output_seqs # run部分 init = tf.global_variables_initializer() X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) with tf.Session() as sess: init.run() Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
packing sequence
n_steps = 2
n_inputs = 3
n_neurons = 5
# 输入是一个三维tensor,none是mini-batch大小不限,n_steps是序列长度 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) # 把一个高维度n的tensor展开成一个n-1维,降维,这里是3位降到2维列表 # unstack之前要做一个1,2维转置,相当于构造了n_steps个数的列表 X_seqs = tf.unstack(tf.transpose(X, perm=[1, 0, 2])) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
# states是最新状态
output_seqs, states = tf.contrib.rnn.static_rnn( basic_cell, X_seqs, dtype=tf.float32)
# 再做一个转置,和输入对应
outputs = tf.transpose(tf.stack(output_seqs), perm=[1, 0, 2])
# 输入大小4*2*3
X_batch = np.array([
# t = 0 t = 1
[[0, 1, 2], [9, 8, 7]], # instance 0
[[3, 4, 5], [0, 0, 0]], # instance 1
[[6, 7, 8], [6, 5, 4]], # instance 2
[[9, 0, 1], [3, 2, 1]], # instance 3
])
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
# output_val是一个4*2*5,仅输出维度神经元个数改变
3. dynamic RNN
本身支持高维tensor输入,内嵌一个循环运行足够多次数的cell,不需要unstack步骤。
这个内嵌循环while_loop()在前向传播中将每次迭代的tensor值存储下来,以便于反向传播过程中使用其计算梯度值。
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) # 动态RNN内部封装一个循环 # 根据输入,动态决定自己需要展开几次 basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
dynamicRNN可以动态规定输入大小(就像句子输入)
n_steps = 2 n_inputs = 3 n_neurons = 5 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) seq_length = tf.placeholder(tf.int32, [None]) outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32, sequence_length=seq_length) init = tf.global_variables_initializer() # X_batch的大小4*2*3 X_batch = np.array([ # step 0 step 1 [[0, 1, 2], [9, 8, 7]], # instance 1 [[3, 4, 5], [0, 0, 0]], # instance 2 (padded with zero vectors) [[6, 7, 8], [6, 5, 4]], # instance 3 [[9, 0, 1], [3, 2, 1]], # instance 4 ]) # 这里设置sequence大小,一共4个batch,第二维上只取第一个 seq_length_batch = np.array([2, 1, 2, 2]) with tf.Session() as sess: init.run() outputs_val, states_val = sess.run( [outputs, states], feed_dict={X: X_batch, seq_length: seq_length_batch})
如果事先不知道输出序列的长度,就需要定义一个end-of-sequence token(eos token),无论是课上还是网上相关信息都很少,这里就不展开了。。
四、RNN训练
RNN比较难以训练,但是如下图的节点中,cost function就包含y2,y3,y4三个输出,往回回溯。
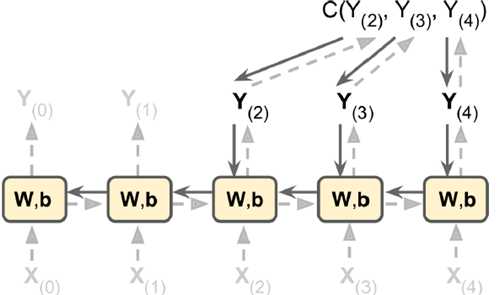
以下MINIST中使用150个RNN神经元,最后加一个全连接层,得到10个神经元的输出(分别对应0-9),最后看对应在
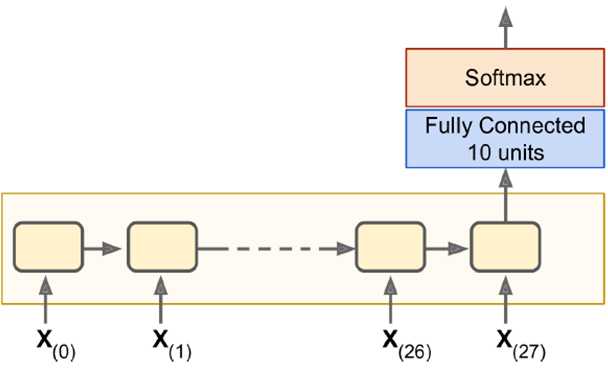
from tensorflow.contrib.layers import fully_connected n_steps = 28 n_inputs = 28 n_neurons = 150 n_outputs = 10 learning_rate = 0.001 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) # 一维输出 y = tf.placeholder(tf.int32, [None]) # 使用最简单的basicRNNcell basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) #使用dynamic_rnn outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32) # 原始输出 logits = fully_connected(states, n_outputs, activation_fn=None) # 计算和真实的交叉熵 xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits) loss = tf.reduce_mean(xentropy) # 使用AdamOptimizer optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) # 计算准确率,只有等于y才是对的,其他都错 correct = tf.nn.in_top_k(logits, y, 1) accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) init = tf.global_variables_initializer() from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("/tmp/data/") # 转换到合理的输入shape X_test = mnist.test.images.reshape((-1, n_steps, n_inputs)) y_test = mnist.test.labels # run100遍,每次处理150个输入 n_epochs = 100 batch_size = 150 # 开始循环 with tf.Session() as sess: init.run() for epoch in range(n_epochs): for iteration in range(mnist.train.num_examples // batch_size): # 读入数据并reshape X_batch, y_batch = mnist.train.next_batch(batch_size) X_batch = X_batch.reshape((-1, n_steps, n_inputs)) # X大写,y小写 sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch}) acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test}) # 每次打印一下当前信息 print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
以下,只用了150个参数,做了单层。就可以达到非常高的效果,可以看出rnn效果非常不错
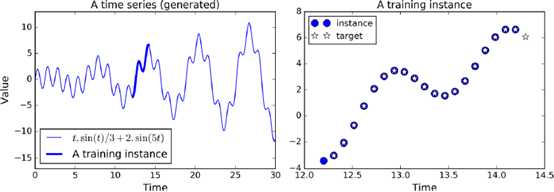
序列预测,前20个状态作为输入,则第2个到21个作为输出,作为训练集
# 输入x0-x19 n_steps = 20 # 只预测一个值 n_inputs = 1 # rnn有100个 n_neurons = 100 n_outputs = 1 # none表示min_batch大小这里任意 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) y = tf.placeholder(tf.float32, [None, n_steps, n_outputs]) cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu) outputs, states = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)
如上代码中,每次输出的vector都是100维的,加入一个output rejections后,使得每次只输出1个值
output rejection实现代码如下
# 设置输出为上面设定的n_outputs大小 cell = tf.contrib.rnn.OutputProjectionWrapper( tf.contrib.rnn.BasicRNNCell(num_units=n_neurons, activation=tf.nn.relu), output_size=n_outputs) learning_rate = 0.001 loss = tf.reduce_mean(tf.square(outputs - y)) optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) init = tf.global_variables_initializer() # 开始训练 n_iterations = 10000 batch_size = 50 with tf.Session() as sess: init.run() for iteration in range(n_iterations): X_batch, y_batch = [...] # fetch the next training batch sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) if iteration % 100 == 0: mse = loss.eval(feed_dict={X: X_batch, y: y_batch}) print(iteration, "\\tMSE:", mse)
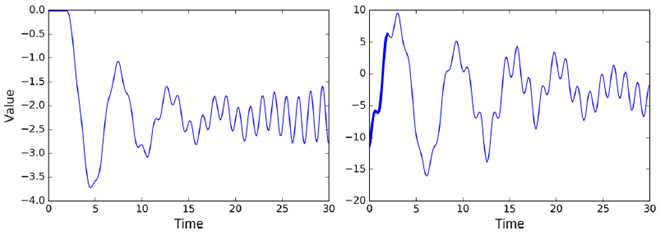
当一个RNN训练好后,它就可以生成很多新的东西。RNN的强大的生成能力非常有魅力,用很多曲子去训练它,它就可以生成新的曲子,用很多文章训练它,他就可以生成新的文章。如果可以训练出功能非常强的RNN模型,就有可能代替人的工作。
with tf.Session() as sess: # 导入训练好的模型 saver.restore(sess, "./my_time_series_model") # 生成新的曲线 sequence = [0.] * n_steps for iteration in range(300): X_batch = np.array(sequence[-n_steps:]).reshape(1, n_steps, 1) y_pred = sess.run(outputs, feed_dict={X: X_batch}) sequence.append(y_pred[0, -1, 0])
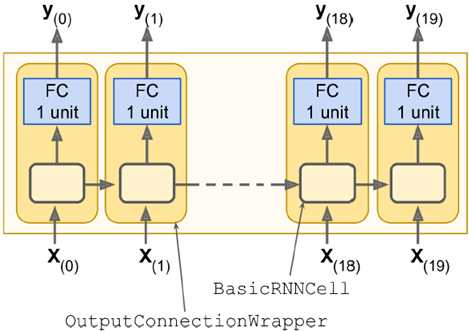
RNN也可以不断叠加,形成很深的网络,如下图所示,每一层输出都反馈到当前位置的输入,时间轴展开后,如右边所示。
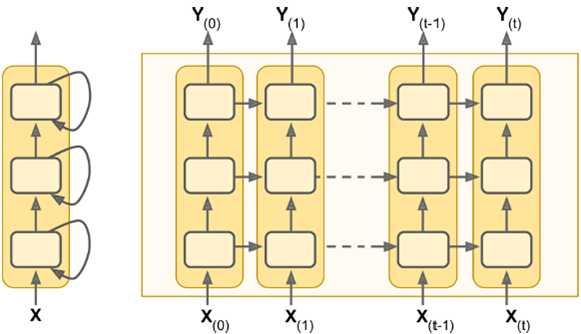
n_inputs = 2 n_steps = 5 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) n_neurons = 100 n_layers = 3 # 做了3层rnn # 模型不是越复杂越好,越复杂所需数据量越大,否则会有过拟合的风险 # 可以加dropout来控制 layers = [tf.contrib.rnn.BasicRNNCell(num_units=n_neurons) for layer in range(n_layers)] multi_layer_cell = tf.contrib.rnn.MultiRNNCell(layers) outputs, states = tf.nn.dynamic_rnn(multi_layer_cell, X, dtype=tf.float32) init = tf.global_variables_initializer() X_batch = np.random.rand(2, n_steps, n_inputs) with tf.Session() as sess: init.run() outputs_val, states_val = sess.run([outputs, states], feed_dict={X: X_batch})
五、困难及优化
反向训练时,对于RNN来说,要横向往前推,一直往前推到序列开始的地方。当序列非常长时,梯度消失,梯度爆炸都与路径长度太长有关,前面的权重都基本固定不变,没有训练效果。
为了解决这个困难,有了很多更复杂RNN模型的提出
1.LSTM(Long Short Term Memory)
97年提出,直到深度学习提出,使用LSTM做出具体实事后,才火起来。或许是因为现在有大数据的环境,以及训练能力很强的硬件这些客观条件得具备,才能真正发挥LSTM的威力。
它把训练信息分为长期记忆(c)和短期记忆(h),上面的长期记忆信息,可以穿到很远,即使序列长到1000,也可以向前传导。
它分了很多个门(gate),输出信息趋近于0,门关闭,趋近于1门打开。i是输入门控制新输入加多少到长期记忆中,f是forget控制是否受长期记忆的影响,哪些长期记忆被忘掉,o是输出门控制哪些长期记忆可以输出并作为短期记忆ht传递下去,通过这3个门控制信息的流动。
可以保证长期记忆变换的缓慢,相对稳定,可以对距离比较远的序列影响,ht和ht-1可以看到距离也比较远,短期记忆ht-1变化明显。
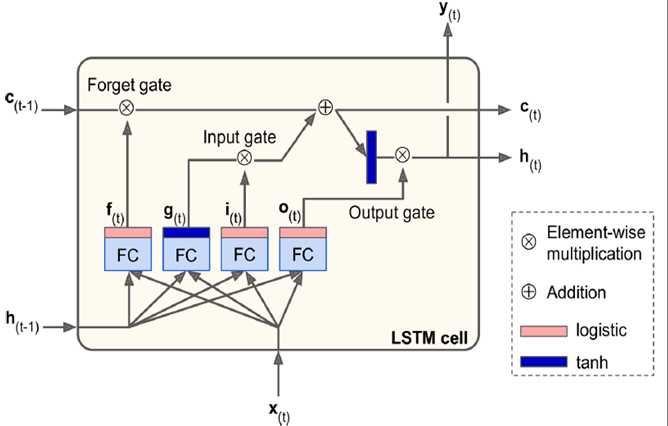
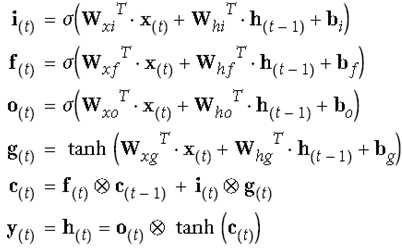
# TensorFlow中LSTM具体实现 n_steps = 28 n_inputs = 28 n_neurons = 150 n_outputs = 10 n_layers = 3 learning_rate = 0.001 X = tf.placeholder(tf.float32, [None, n_steps, n_inputs]) y = tf.placeholder(tf.int32, [None]) lstm_cells = [tf.contrib.rnn.BasicLSTMCell(num_units=n_neurons) for layer in range(n_layers)] multi_cell = tf.contrib.rnn.MultiRNNCell(lstm_cells) outputs, states = tf.nn.dynamic_rnn(multi_cell, X, dtype=tf.float32) top_layer_h_state = states[-1][1] logits = tf.layers.dense(top_layer_h_state, n_outputs, name="softmax") xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits) loss = tf.reduce_mean(xentropy, name="loss") optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate) training_op = optimizer.minimize(loss) correct = tf.nn.in_top_k(logits, y, 1) accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) init = tf.global_variables_initializer()
LSTM还有一点改进Peephole Connection
lstm_cell = tf.contrib.rnn.LSTMCell(num_units=n_neurons, use_peepholes=True)
2. GRU(Gated recurrent unit)
GRU是对LSTM简化后的版本,去掉了长短期记忆的区分(都是h),减少了几个门,2014年提出,从参数上来说较LSTM简单些。
统一用update gate控制原来的i门和f门。z趋近于0就用ht-1来更新,趋近于1就取当前输入。
比LSTM还少一个矩阵乘法,实际表现不比LSTM差,也成为现在很多研究者越来越看重的方法。
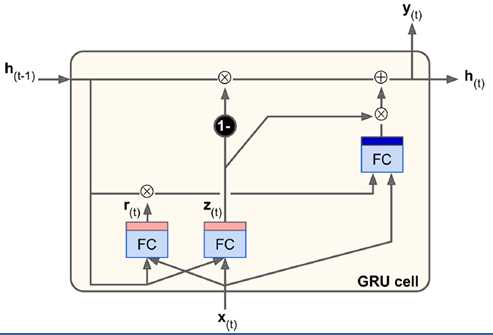
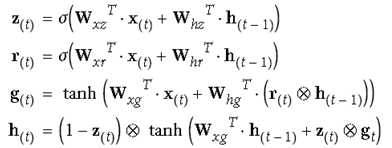
调用时,直接调用GRU cell即可
gru_cell = tf.contrib.rnn.GRUCell(num_units=n_neurons)
六、RNN在NLP(natural language processing)中的应用
RNN的输入原本是one-hot的表示,但这样会使得输入极其稀疏,不好训练。于是将高维空间映射到低维(如100维)空间,用这个低维嵌入的输入做训练,非常有效。
Word Embeddings
相同含义的词在低维空间中距离近,含义差的多的离得远。
# 把50000维数据映射到150维数据空间上 vocabulary_size = 50000 embedding_size = 150 # 做一个全连接 embeddings = tf.Variable(tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0)) train_inputs = tf.placeholder(tf.int32, shape=[None]) # from ids embed = tf.nn.embedding_lookup(embeddings, train_inputs)# to embd
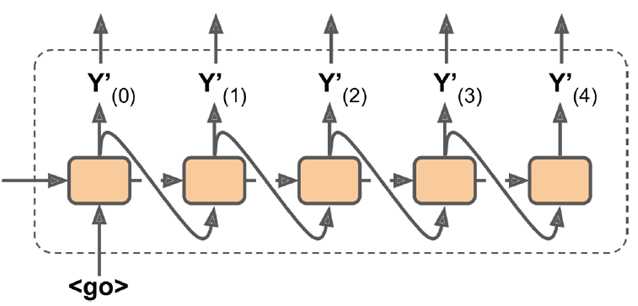
例如下图所示,把要翻译的英文句子做输入,用训练后的状态值做输入,和法语作为训练集的作为decoder输入。第一位放一个起始信号<go>,输出和输入刚好错一位,最后一位以一个结束标识<eos>结束。这样做是为了后继应用时,翻译新句子没有training label,只有英文输入。把英文输入放进来后加一个<go>,得到第一个je输出,把第一个词放进来得到第二个输出bois。。最后<eos>翻译结束。
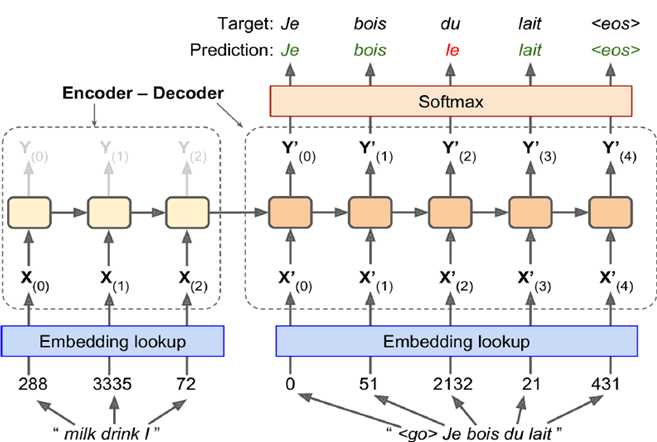
最后实际应用时如下,输入<go>开始翻译。