归并排序6$堆排序图解7

Posted 2021-05-01 taoisall

归并排序基本思想:

归并排序就是利用归并的思想实现的排序方法。而且充分利用了完全二叉树的深度是的特性，因此效率比较高。其基本原理如下：对于给定的一组记录，利用递归与分治技术将数据序列划分成为越来越小的半子表，在对半子表排序，最后再用递归方法将排好序的半子表合并成为越来越大的有序序列。

经过第一轮比较后得到最小的记录，然后将该记录的位置与第一个记录的位置交换；接着对不包括第一个记录以外的其他记录进行第二次比较，得到最小记录并与第二个位置记录交换；重复该过程，知道进行比较的记录只剩下一个为止。

参考: https://blog.csdn.net/jianyuerensheng/article/details/51262984

原理:

（1）申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

（2）设定两个指针，最初位置分别为两个已经排序序列的起始位置

（3）比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

（4）重复步骤3直到某一指针达到序列尾

（5）将另一序列剩下的所有元素直接复制到合并序列尾

package com.play.pre.sort;

/**

* 各种排序算法详细讲解6 ---归并排序

*/

import java.util.Arrays;

/**

* */

public class sort5 {

   public static void main(String[] args) {

    int [] a={50,10,90,30};//{50,10,90,30,70,40,80,60,20}

       mergeSort(a, 0, a.length - 1);

    System.out.println("排序结果:"+ Arrays.toString(a));

   }

   public static void merge(int[] a, int low, int mid, int high) {

       int[] temp = new int[high - low + 1];

       int i = low;// 左指针

       int j = mid + 1;// 右指针

       int k = 0;

       // 把较小的数先移到新数组中

       while (i <= mid && j <= high) {

           if (a[i] < a[j]) {

               temp[k++] = a[i++];

           } else {

               temp[k++] = a[j++];

           }

       }

       // 把左边剩余的数移入数组

       while (i <= mid) {

           temp[k++] = a[i++];

       }

       // 把右边边剩余的数移入数组

       while (j <= high) {

           temp[k++] = a[j++];

       }

       // 把新数组中的数覆盖nums数组

       for (int k2 = 0; k2 < temp.length; k2++) {

           a[k2 + low] = temp[k2];

       }

   }

   public static void mergeSort(int[] a, int low, int high) {

       int mid = (low + high) / 2; //int mid = low + (high - low)/2      //4

       if (low < high) {

           // 左边

           mergeSort(a, low, mid); // 0  4

           // 右边

           mergeSort(a, mid + 1, high); //5  8

           // 左右归并

           merge(a, low, mid, high);

           System.out.println(Arrays.toString(a));

       }

   }

}

--------------

https://blog.csdn.net/qq_36186690/article/details/82505569  

堆排序：堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

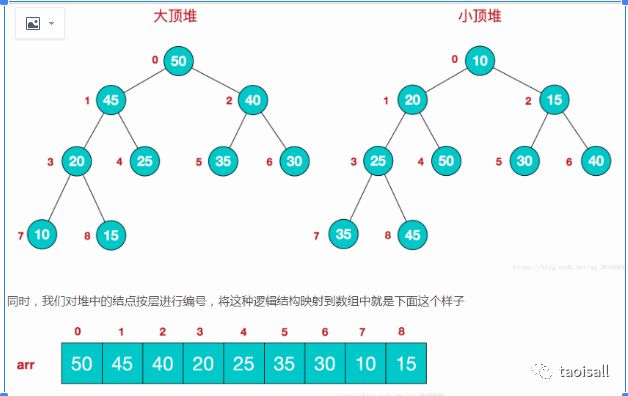
该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

ok，了解了这些定义。接下来，我们来看看堆排序的基本思想及基本步骤：

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

 

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

　　a.假设给定无序序列结构如下

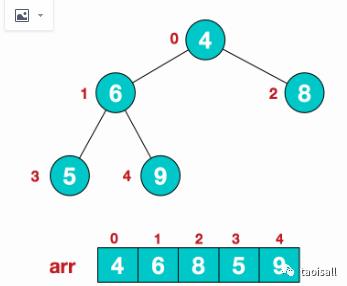
2.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

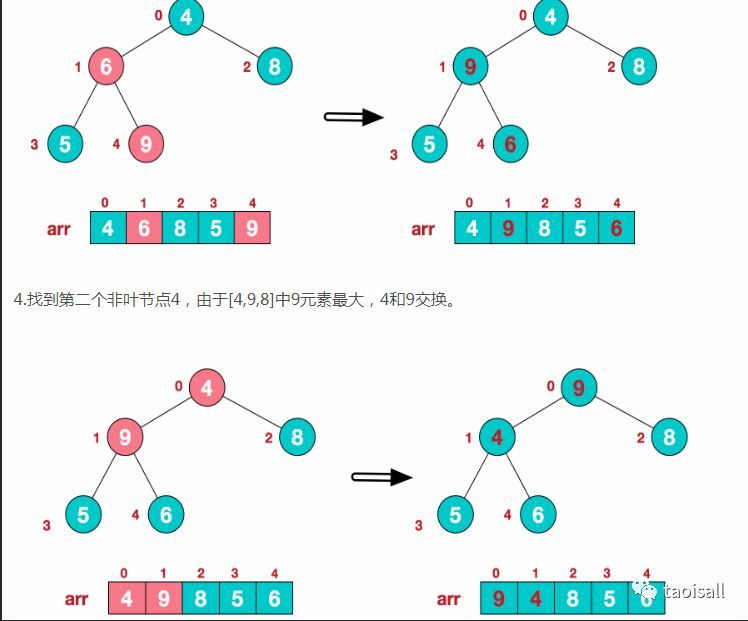
这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

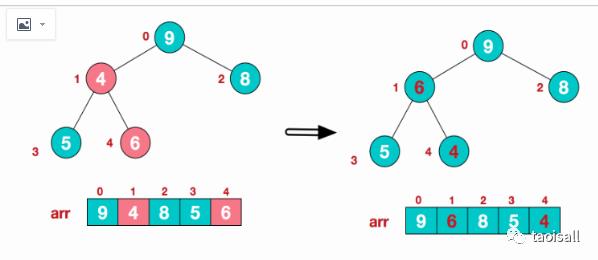
此时，我们就将一个无需序列构造成了一个大顶堆。

步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

a.将堆顶元素9和末尾元素4进行交换

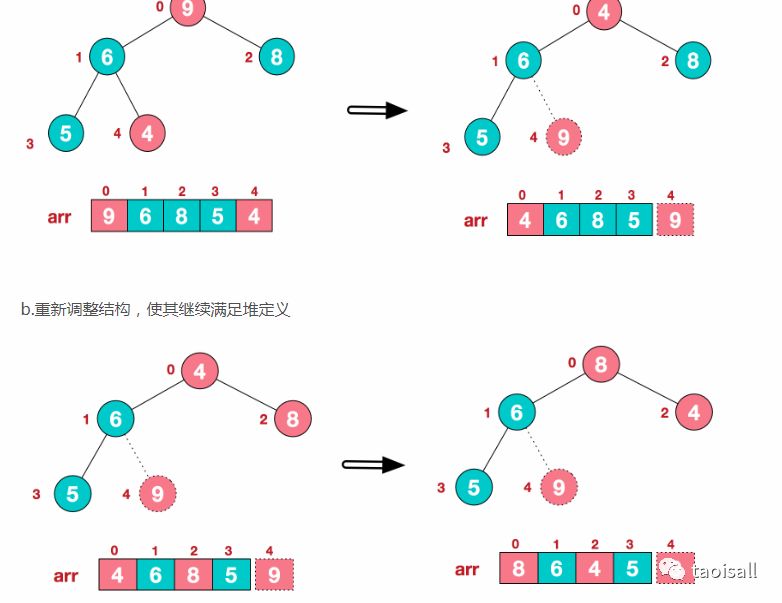
再简单总结下堆排序的基本思路：

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

package com.play.pre.sort;

/**

* 各种排序算法详细讲解6 ---堆排序

*/

import java.util.Arrays;

/**

* */

public class sort6 {

   public static void main(String[] args) {

    int [] a= {7,6,7,11,5,12,3,0,1};

       sort(a);

    System.out.println("排序结果:"+ Arrays.toString(a));

   }

   public static void sort(int []arr){

       //1.构建大顶堆

       for(int i=arr.length/2-1;i>=0;i--){

           //从第一个非叶子结点从下至上，从右至左调整结构

           adjustHeap(arr,i,arr.length);

       }

       //2.调整堆结构+交换堆顶元素与末尾元素

       for(int j=arr.length-1;j>0;j--){

           swap(arr,0,j);//将堆顶元素与末尾元素进行交换

           adjustHeap(arr,0,j);//重新对堆进行调整

       }

   }

   /**

    * 调整大顶堆（仅是调整过程，建立在大顶堆已构建的基础上）

    * @param arr

    * @param i

    * @param length

    */

   public static void adjustHeap(int []arr,int i,int length){

       int temp = arr[i];//先取出当前元素i

       for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始，也就是2i+1处开始

           if(k+1<length && arr[k]<arr[k+1]){//如果左子结点小于右子结点，k指向右子结点

               k++;

           }

           if(arr[k] >temp){//如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）

               arr[i] = arr[k];

               i = k;

           }else{

               break;

           }

       }

       arr[i] = temp;//将temp值放到最终的位置

   }

   /**

    * 交换元素

    * @param arr

    * @param a

    * @param b

    */

   public static void swap(int []arr,int a ,int b){

       int temp=arr[a];

       arr[a] = arr[b];

       arr[b] = temp;

   }

}