图解程序员必须掌握的Java常用8大排序算法
Posted AaronBear
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图解程序员必须掌握的Java常用8大排序算法相关的知识,希望对你有一定的参考价值。
这篇文章主要介绍了Java如何实现八个常用的排序算法:插入排序、冒泡排序、选择排序、希尔排序 、快速排序、归并排序、堆排序和LST基数排序,分享给大家一起学习。
分类
1)插入排序(直接插入排序、希尔排序)
2)交换排序(冒泡排序、快速排序)
3)选择排序(直接选择排序、堆排序)
4)归并排序
5)分配排序(基数排序)
所需辅助空间最多:归并排序
所需辅助空间最少:堆排序
平均速度最快:快速排序
不稳定:快速排序,希尔排序,堆排序。
先来看看8种排序之间的关系:
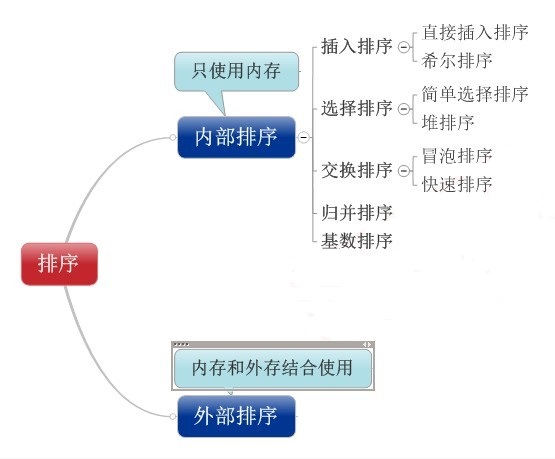
1.直接插入排序
(1)基本思想:在要排序的一组数中,假设前面(n-1)[n>=2] 个数已经是排
好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数
也是排好顺序的。如此反复循环,直到全部排好顺序。
(2)实例

(3)用java实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
package com.njue; publicclass insertSort { public insertSort(){ inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51}; int temp=0; for(int i=1;i<a.length;i++){ int j=i-1; temp=a[i]; for(;j>=0&&temp<a[j];j--){ a[j+1]=a[j]; //将大于temp的值整体后移一个单位 } a[j+1]=temp; } for(int i=0;i<a.length;i++){ System.out.println(a[i]); } } |
2. 希尔排序(最小增量排序)
(1)基本思想:算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。
(2)实例:
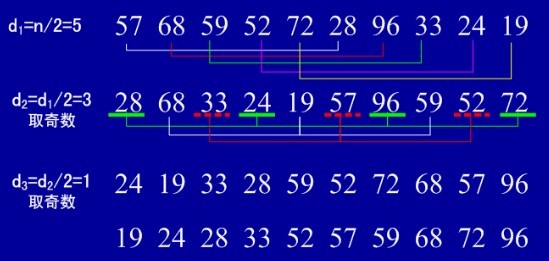
(3)用java实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
publicclass shellSort { publicshellSort(){ int a[]={1,54,6,3,78,34,12,45,56,100}; double d1=a.length; int temp=0; while(true){ d1= Math.ceil(d1/2); int d=(int) d1; for(int x=0;x<d;x++){ for(int i=x+d;i<a.length;i+=d){ int j=i-d; temp=a[i]; for(;j>=0&&temp<a[j];j-=d){ a[j+d]=a[j]; } a[j+d]=temp; } } if(d==1){ break; } for(int i=0;i<a.length;i++){ System.out.println(a[i]); } } |
3.简单选择排序
(1)基本思想:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;
然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
(2)实例:

(3)用java实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public class selectSort { public selectSort(){ int a[]={1,54,6,3,78,34,12,45}; int position=0; for(int i=0;i<a.length;i++){ int j=i+1; position=i; int temp=a[i]; for(;j<a.length;j++){ if(a[j]<temp){ temp=a[j]; position=j; } } a[position]=a[i]; a[i]=temp; } for(int i=0;i<a.length;i++) System.out.println(a[i]); } } |
4.堆排序
(1)基本思想:堆排序是一种树形选择排序,是对直接选择排序的有效改进。
堆的定义如下:具有n个元素的序列(h1,h2,…,hn),当且仅当满足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1)(i=1,2,…,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最大项(大顶堆)。完全二叉树可以很直观地表示堆的结构。堆顶为根,其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树,调整它们的存储序,使之成为一个堆,这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数,二是反复调用渗透函数实现排序的函数。
(2)实例:
初始序列:46,79,56,38,40,84
建堆:
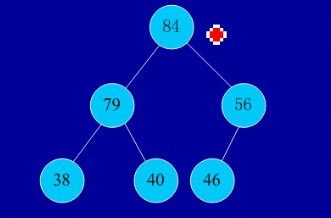
交换,从堆中踢出最大数
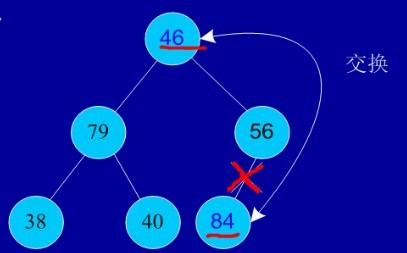
剩余结点再建堆,再交换踢出最大数
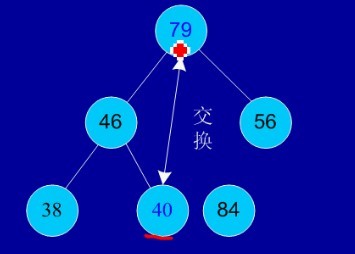
依次类推:最后堆中剩余的最后两个结点交换,踢出一个,排序完成。
(3)用java实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
import java.util.Arrays; publicclass HeapSort { inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51}; public HeapSort(){ heapSort(a); } public void heapSort(int[] a){ System.out.println("开始排序"); int arrayLength=a.length; //循环建堆 for(int i=0;i<arrayLength-1;i++){ //建堆 buildMaxHeap(a,arrayLength-1-i); //交换堆顶和最后一个元素 swap(a,0,arrayLength-1-i); System.out.println(Arrays.toString(a)); } } private void swap(int[] data, int i, int j) { // TODO Auto-generated method stub int tmp=data[i]; data[i]=data[j]; data[j]=tmp; } //对data数组从0到lastIndex建大顶堆 privatevoid buildMaxHeap(int[] data, int lastIndex) { // TODO Auto-generated method stub //从lastIndex处节点(最后一个节点)的父节点开始 for(int i=(lastIndex-1)/2;i>=0;i--){ //k保存正在判断的节点 int k=i; //如果当前k节点的子节点存在 while(k*2+1<=lastIndex){ //k节点的左子节点的索引 int biggerIndex=2*k+1; //如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在 if(biggerIndex<lastIndex){ //若果右子节点的值较大 if(data[biggerIndex]<data[biggerIndex+1]){ //biggerIndex总是记录较大子节点的索引 biggerIndex++; } } //如果k节点的值小于其较大的子节点的值 if(data[k]<data[biggerIndex]){ //交换他们 swap(data,k,biggerIndex); //将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值 k=biggerIndex; }else{ break; } } } } } |
5.冒泡排序
(1)基本思想:在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
(2)实例:

(3)用java实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public class bubbleSort { publicbubbleSort(){ inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51}; int temp=0; for(int i=0;i<a.length-1;i++){ for(int j=0;j<a.length-1-i;j++){ if(a[j]>a[j+1]){ temp=a[j]; a[j]=a[j+1]; a[j+1]=temp; } } } for(int i=0;i<a.length;i++){ System.out.println(a[i]); } } |
6.快速排序
(1)基本思想:选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
(2)实例:

(3)用java实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
publicclass quickSort { inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51}; publicquickSort(){ quick(a); for(int i=0;i<a.length;i++){ System.out.println(a[i]); } } publicint getMiddle(int[] list, int low, int high) { int tmp =list[low]; //数组的第一个作为中轴 while (low < high){ while (low < high&& list[high] >= tmp) { high--; } list[low] =list[high]; //比中轴小的记录移到低端 while (low < high&& list[low] <= tmp) { low++; } list[high] =list[low]; //比中轴大的记录移到高端 } list[low] = tmp; //中轴记录到尾 return low; //返回中轴的位置 } publicvoid _quickSort(int[] list, int low, int high) { if (low < high){ int middle =getMiddle(list, low, high); //将list数组进行一分为二 _quickSort(list, low, middle - 1); //对低字表进行递归排序 _quickSort(list,middle + 1, high); //对高字表进行递归排序 } } publicvoid quick(int[] a2) { if (a2.length > 0) { //查看数组是否为空 _quickSort(a2,0, a2.length - 1); } } } |
7、归并排序
(1)基本排序:归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
(2)实例:

(3)用java实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
import java.util.Arrays; publicclass mergingSort { inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51}; Java常用排序算法/程序员必须掌握的8大排序算法
|