数据结构之线段树(Segment Tree)

Posted 2023-02-23 WSYW126

线段树的概念

线段树(Segment Tree)也是一棵树，只不过元素的值代表一个区间。
常用区间的 统计 操作，比如一个区间的最大值(max)，最小值(min)，和(sum)等等。

线段树是一种平衡二叉搜索树(完全二叉树)，它将一个线段区间划分成一些单元区间。对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]，最后的叶子节点数目为N，与数组下标对应。线段树 的一般包括建立、查询、插入、更新等操作，建立规模为N的时间复杂度是 O(NlogN)，其他操作时间复杂度为O(logN)。

 

分段树是完全二叉树，可以用一维数组存储。

如果我们用数组来存储线段树的话，我们大致需要开辟多大的数组空间呢？

根据而前面我们对满二叉树的分析

h层的满二叉树总共有 2^h-1 个节点，第h-1层有2^(h-1)个节点，它们大概是两倍的关系。

也就是说对于满二叉树 最后一层的节点数乘以2 大致就是整棵树的节点数。

但是线段树并不一定是满二叉树，但是一定是平衡二叉树，所以需要多冗余一层。也就是 乘以4 就足以盛放所有的节点数，但是会浪费一定的内存空间。

 

线段树的基本操作

构建线段树

根据上面我们对线段树的描述，构建一个线段树就比较简单了，根节点就是整个区间，根节点的左右子树平分根节点的区间，直至区间内只剩下一个元素不能平分为止。

修改线段树

针对上面的数组，把索引为 2 的值改成 10 如下图所示

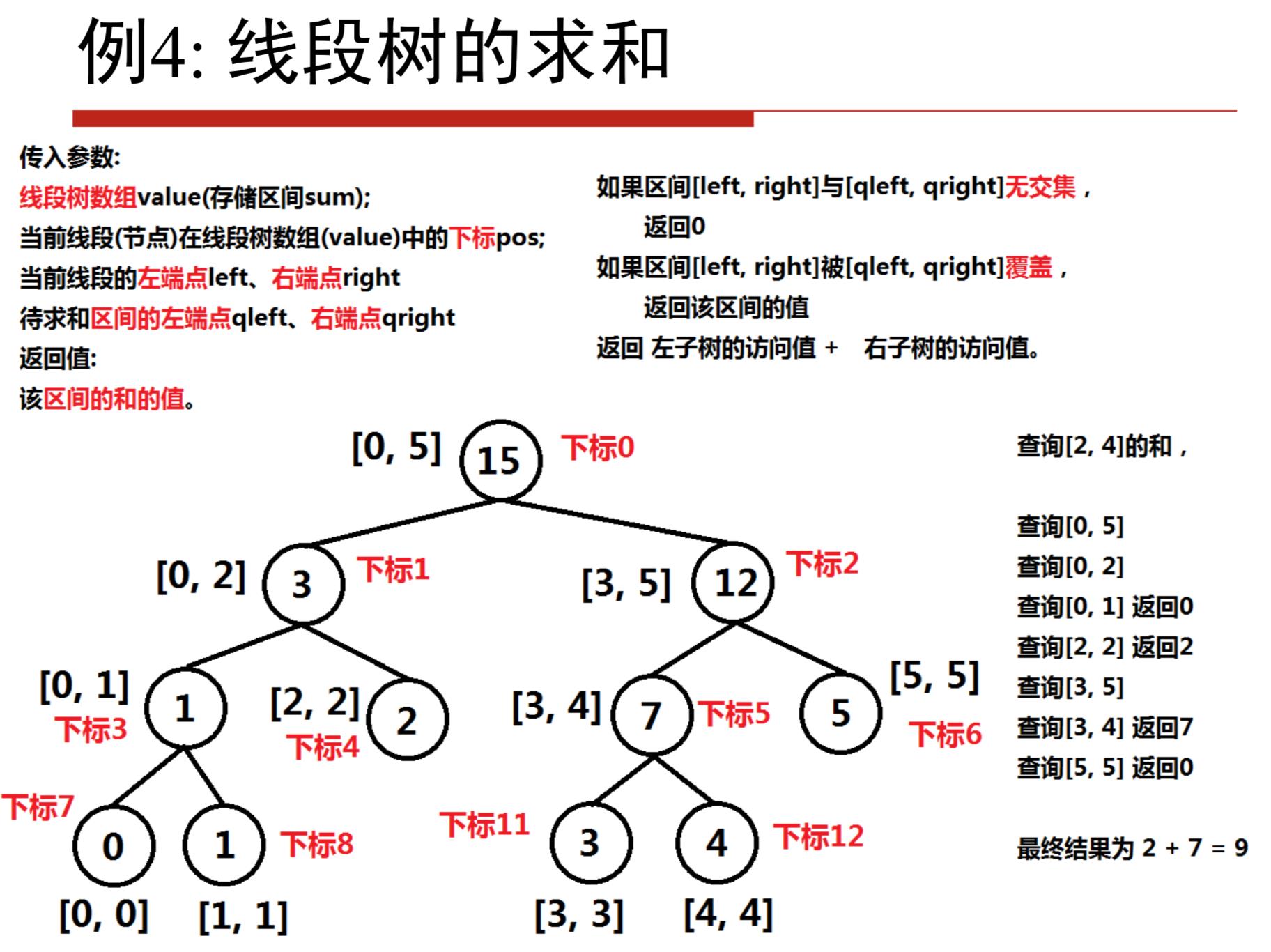
线段树的查询

对于线段树的查询，主要有以下几种情况：

• 要查询的区间在刚好就是当前节点的区间
• 要查找的区间在当前节点的左子树区间
• 要查找的区间在当前节点的右子树区间
• 要查找的区间一部分在当前节点的左子树区间，一部分在右子树区间

 

实现一个线段树

下面实现的线段树，有三个功能：

• 把数组构建成一颗线段树
• 线段树的修改
• 线段树的查询

/**
 * @author yangjunpeng
 * @version $Id: ArraySegmentTree.java, v 0.1 2020年04月08日 下午10:38 yangjunpeng Exp $
 */
public class ArraySegmentTree<T> 

    private T         tree[];
    private T         data[];

    private Merger<T> merger;

    public interface Merger<T> 
        T merge(T a, T b);
    

    public ArraySegmentTree(T[] arr, Merger<T> merger) 
        this.merger = merger;
        data = (T[]) new Object[arr.length];
        for (int i = 0; i < data.length; i++) 
            data[i] = arr[i];
        

        this.tree = (T[]) new Object[data.length * 4];
        buildSegmentTree(0, 0, data.length - 1);

    

    /**
     * 构建线段树
     *
     * @param treeIndex 当前需要添加节点的索引
     * @param treeLeft  treeIndex左边界
     * @param treeRight treeIndex右边界
     */
    private void buildSegmentTree(int treeIndex, int treeLeft, int treeRight) 
        if (treeLeft == treeRight) 
            tree[treeIndex] = data[treeLeft];
            return;
        
        //当前节点左子树索引
        int leftTreeIndex = getLeft(treeIndex);
        //当前节点右子树索引
        int rightTreeIndex = getRight(treeIndex);
        //int mid = (left+right)/2; 如果left和right很大，可能会导致整型溢出
        int mid = treeLeft + (treeRight - treeLeft) / 2;
        //构建左子树
        buildSegmentTree(leftTreeIndex, treeLeft, mid);
        //构建右子树
        buildSegmentTree(rightTreeIndex, mid + 1, treeRight);
        //当前节点存放的值
        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);

    

    public T query(int start, int end) 
        return query(0, 0, data.length - 1, start, end);
    

    /**
     * @param treeIndex 当前查找的节点
     * @param treeLeft  treeIndex的左边界
     * @param treeRight treeIndex的右边界
     * @param queryL    用户需要查找的左边界
     * @param queryR    用户需要查找的右边界
     * @return
     */
    private T query(int treeIndex, int treeLeft, int treeRight, int queryL, int queryR) 

        //1, 需要查找的范围完刚好在这个treeIndex节点的区间
        if (treeLeft == queryL && treeRight == queryR) 
            return tree[treeIndex];
        

        //当前节点的区间的中间点
        int mid = treeLeft + (treeRight - treeLeft) / 2;
        //左子树索引
        int leftTreeIndex = getLeft(treeIndex);
        //右子树索引
        int rightTreeIndex = getRight(treeIndex);

        //2, 需要查找的范围完全在左子树的区间里
        if (queryR <= mid) 
            return query(leftTreeIndex, treeLeft, mid, queryL, queryR);
        
        //3, 需要查找的范围完全在右子树区间里
        if (queryL >= mid + 1) 
            return query(rightTreeIndex, mid + 1, treeRight, queryL, queryR);
        

        //需要查找的范围一部分在左子树里，一部分在右子树中
        T left = query(leftTreeIndex, treeLeft, mid, queryL, mid);
        T right = query(rightTreeIndex, mid + 1, treeRight, mid + 1, queryR);
        return merger.merge(left, right);
    

    public void update(int index, T e) 
        data[index] = e;
        update(0, 0, data.length - 1, index, e);
    

    private void update(int treeIndex, int treeLeft, int treeRight, int index, T e) 
        if (treeLeft == treeRight) 
            tree[treeIndex] = e;
            return;
        

        int mid = treeLeft + (treeRight - treeLeft) / 2;
        int leftChildIndex = getLeft(treeIndex);
        int rightChildIndex = getRight(treeIndex);

        if (index <= mid) 
            update(leftChildIndex, treeLeft, mid, index, e);
         else if (index >= mid + 1) 
            update(rightChildIndex, mid + 1, treeRight, index, e);
        

        //更改完叶子节点后，还需要对他的所有祖辈节点更新
        tree[treeIndex] = merger.merge(tree[leftChildIndex], tree[rightChildIndex]);
    

    public T get(int index) 
        return data[0];
    

    public int size() 
        return data.length;
    

    public int getLeft(int index) 
        return index * 2 + 1;
    

    public int getRight(int index) 
        return index * 2 + 2;
    

    @Override
    public String toString() 
        StringBuilder builder = new StringBuilder();
        builder.append("[");
        for (int i = 0; i < tree.length; i++) 
            if (tree[i] == null) 
                continue;
            
            builder.append(tree[i]).append(',');
        
        builder.deleteCharAt(builder.length() - 1);
        builder.append(']');
        return builder.toString();
    

 

leetcode 307题：

https://leetcode-cn.com/problems/range-sum-query-mutable/

class NumArray 

    ArraySegmentTree arraySegmentTree = null;

    public NumArray(int[] nums) 
        arraySegmentTree = new ArraySegmentTree(nums);
    

    public void update(int i, int val) 
        if (arraySegmentTree.data.length == 0) 
            return ;
        
        arraySegmentTree.update(i, val);
    

    public int sumRange(int i, int j) 
        if (arraySegmentTree.data.length == 0) 
            return 0;
        
        Integer query = arraySegmentTree.query(i, j);
        return query;
    

    public static class ArraySegmentTree 

        private int tree[];
        private int data[];

        public ArraySegmentTree(int[] arr) 
            data = new int[arr.length];
            for (int i = 0; i < data.length; i++) 
                data[i] = arr[i];
            

            this.tree = new int[data.length * 4];

            if (data.length != 0) 
                buildSegmentTree(0, 0, data.length - 1);
            

        

        /**
         * 构建线段树
         *
         * @param treeIndex 当前需要添加节点的索引
         * @param treeLeft  treeIndex左边界
         * @param treeRight treeIndex右边界
         */
        private void buildSegmentTree(int treeIndex, int treeLeft, int treeRight) 
            if (treeLeft == treeRight) 
                tree[treeIndex] = data[treeLeft];
                return;
            
            //当前节点左子树索引
            int leftTreeIndex = getLeft(treeIndex);
            //当前节点右子树索引
            int rightTreeIndex = getRight(treeIndex);
            //int mid = (left+right)/2; 如果left和right很大，可能会导致整型溢出
            int mid = treeLeft + (treeRight - treeLeft) / 2;
            //构建左子树
            buildSegmentTree(leftTreeIndex, treeLeft, mid);
            //构建右子树
            buildSegmentTree(rightTreeIndex, mid + 1, treeRight);
            //当前节点存放的值
            tree[treeIndex] = tree[leftTreeIndex] + tree[rightTreeIndex];

        

        public int query(int start, int end) 
            return query(0, 0, data.length - 1, start, end);
        

        /**
         * @param treeIndex 当前查找的节点
         * @param treeLeft  treeIndex的左边界
         * @param treeRight treeIndex的右边界
         * @param queryL    用户需要查找的左边界
         * @param queryR    用户需要查找的右边界
         * @return
         */
        private int query(int treeIndex, int treeLeft, int treeRight, int queryL, int queryR) 

            //1, 需要查找的范围完刚好在这个treeIndex节点的区间
            if (treeLeft == queryL && treeRight == queryR) 
                return tree[treeIndex];
            

            //当前节点的区间的中间点
            int mid = treeLeft + (treeRight - treeLeft) / 2;
            //左子树索引
            int leftTreeIndex = getLeft(treeIndex);
            //右子树索引
            int rightTreeIndex = getRight(treeIndex);

            //2, 需要查找的范围完全在左子树的区间里
            if (queryR <= mid) 
                return query(leftTreeIndex, treeLeft, mid, queryL, queryR);
            
            //3, 需要查找的范围完全在右子树区间里
            if (queryL >= mid + 1) 
                return query(rightTreeIndex, mid + 1, treeRight, queryL, queryR);
            

            //需要查找的范围一部分在左子树里，一部分在右子树中
            int left = query(leftTreeIndex, treeLeft, mid, queryL, mid);
            int right = query(rightTreeIndex, mid + 1, treeRight, mid + 1, queryR);
            return left + right;
        

        public void update(int index, int e) 
            data[index] = e;
            update(0, 0, data.length - 1, index, e);
        

        private void update(int treeIndex, int treeLeft, int treeRight, int index, int e) 
            if (treeLeft == treeRight) 
                tree[treeIndex] = e;
                return;
            

            int mid = treeLeft + (treeRight - treeLeft) / 2;
            int leftChildIndex = getLeft(treeIndex);
            int rightChildIndex = getRight(treeIndex);

            if (index <= mid) 
                update(leftChildIndex, treeLeft, mid, index, e);
             else if (index >= mid + 1) 
                update(rightChildIndex, mid + 1, treeRight, index, e);
            

            //更改完叶子节点后，还需要对他的所有祖辈节点更新
            tree[treeIndex] = tree[leftChildIndex] + tree[rightChildIndex];
        

        public int get(int index) 
            return data[0];
        

        public int size() 
            return data.length;
        

        public int getLeft(int index) 
            return index * 2 + 1;
        

        public int getRight(int index) 
            return index * 2 + 2;
        

    

 

参考资料：
https://blog.csdn.net/johnny901114/article/details/80643017

https://blog.csdn.net/qq_28327765/article/details/85210522
备注：
转载请注明出处：https://blog.csdn.net/WSYW126/article/details/105524218
作者：WSYW126