数据结构: 线段树Segment Tree

Posted 2021-12-08 ‍oOoOoOooOO

---

💕写博客的目的在于巩固所学知识💕

---

💕为什么要有线段树

有这样一个场景：给你一个数组nums

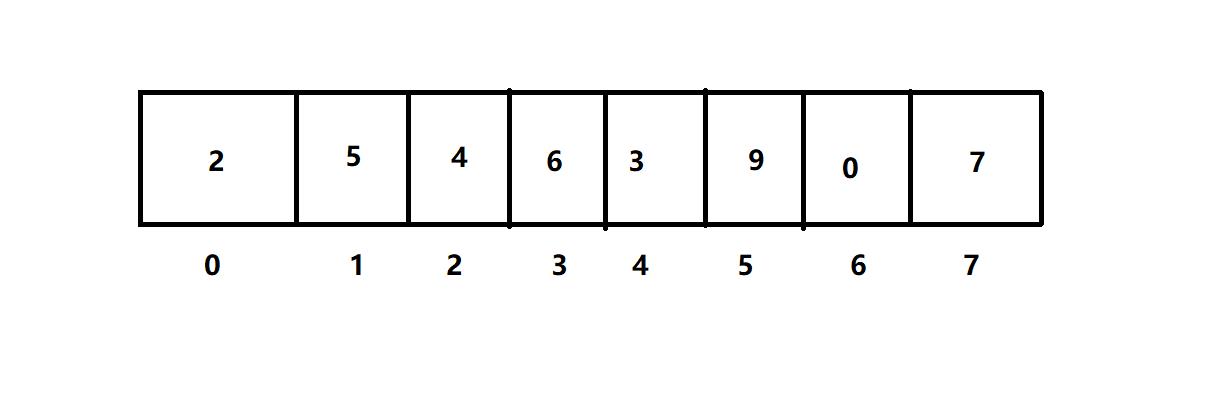
 有两个任务

        1.将 nums[index]的值更新为 val;( 0 =< index < nums.length,val为随机值）

        2.计算子数组 nums[left, right] 的总和（即，nums[left] + nums[left + 1], ...,    nums[right]）

这两个任务会执行若干次，执行的顺序随机。

对于第一个任务，我们可以利用数组的随机访问能力，在时间复杂度O(1)的情况下就能完成。

但对于第二个任务，我们可以采取累加的方式，从nums[left]一直加到nums[right]，时间复杂度为O(n)。

那么问题来了，我们有没有再次基础上进一步的降低时间复杂度？

有！那就是线段树。

线段树的结构

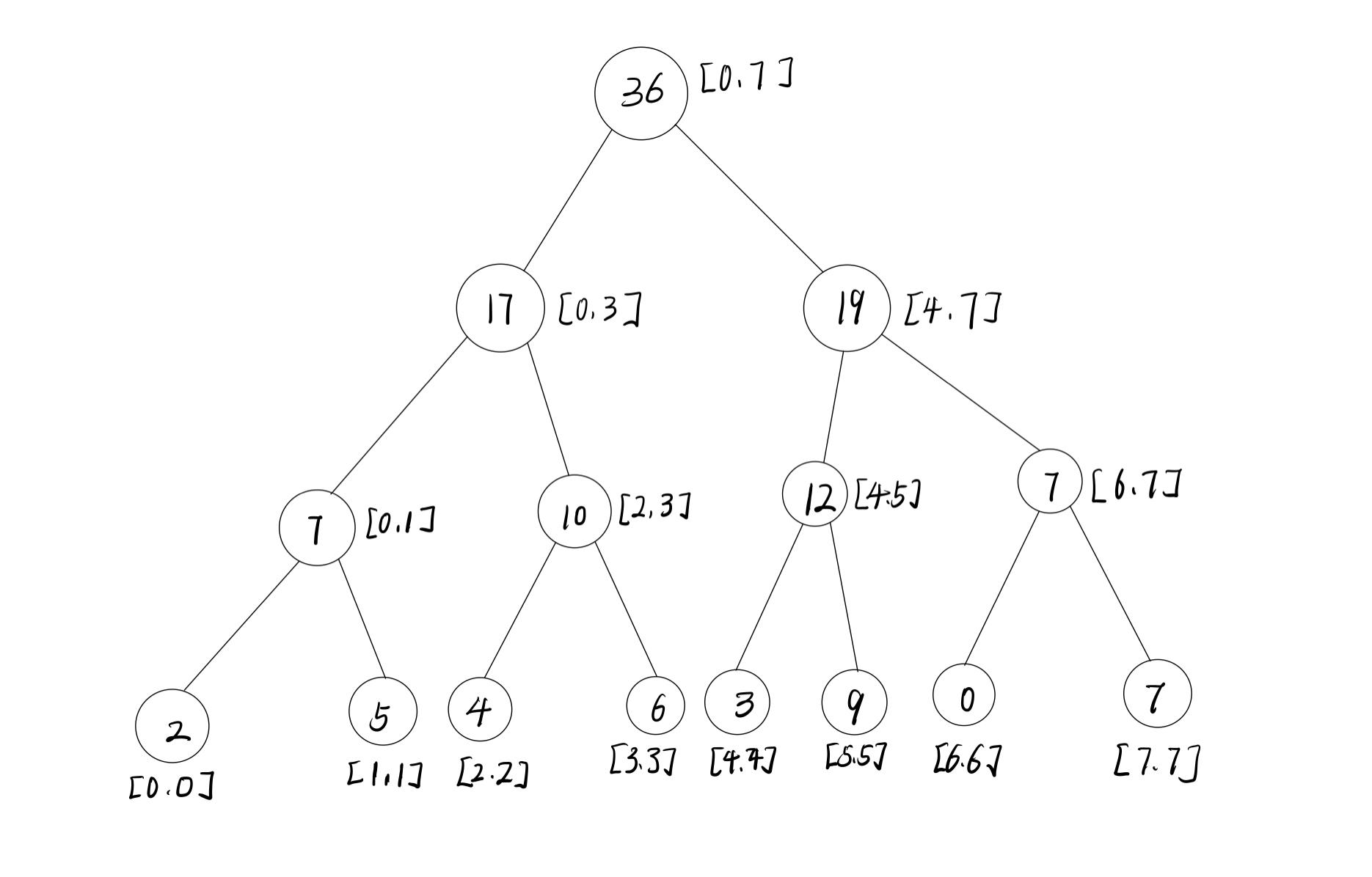
 根据上面的数组我们构成出了这样的树，突然看可能觉得很懵。

我们先从叶子节点看起 

可以看出叶子节点从左到右分别为数组nums[index]的值

再看父节点

可以知道父节点为左右两个子节点之和，则根节点则为整个数组之和。

这个时候，如果要我们计算nums[3,7]子数组之和，我们只需要对二叉树进行遍历，找到图中的两个节点即可。

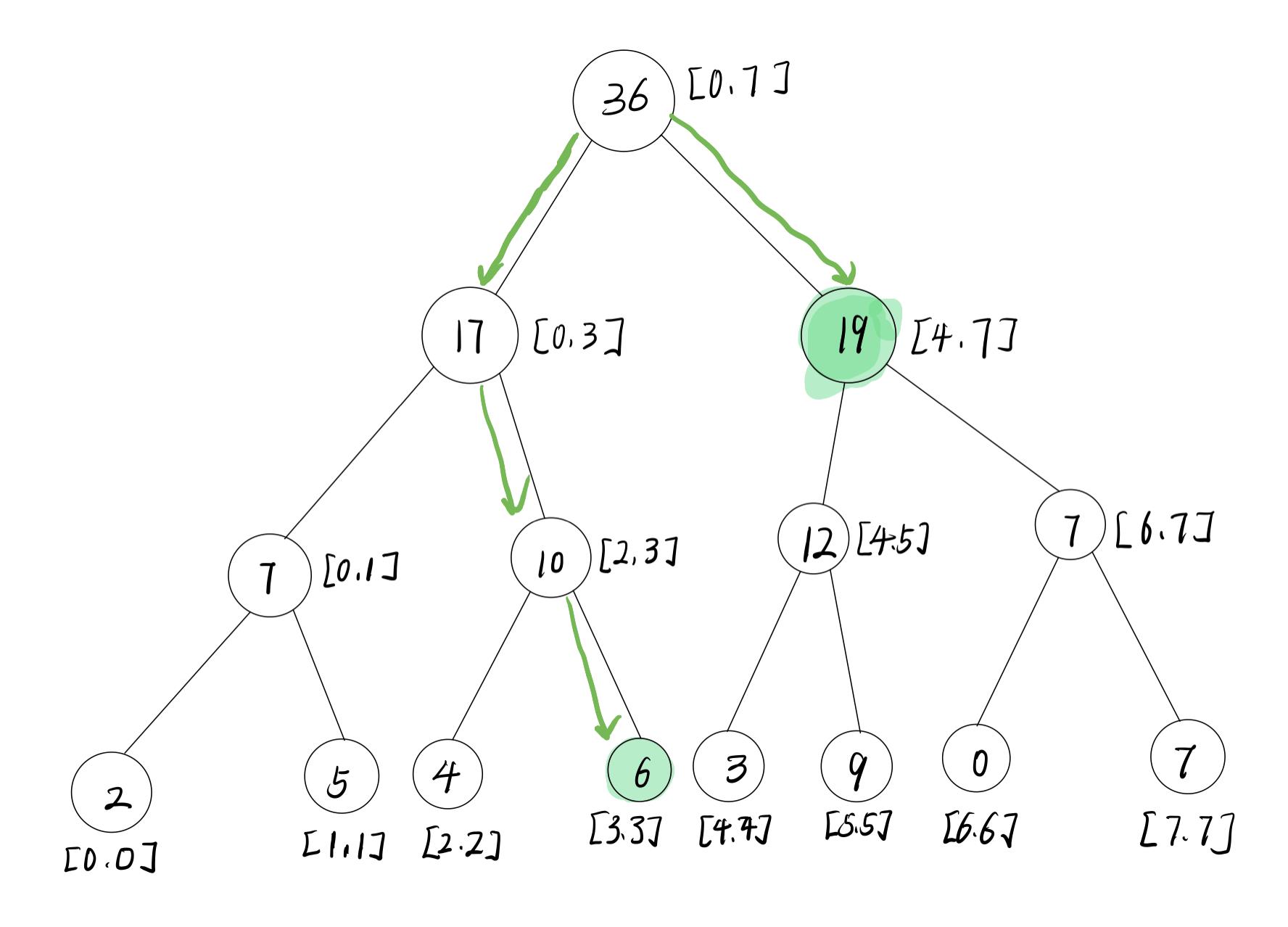
 💕构造线段树

Talk is cheap. Show me the code.

在开始之前，首先要明白线段树其实是一个数状数组

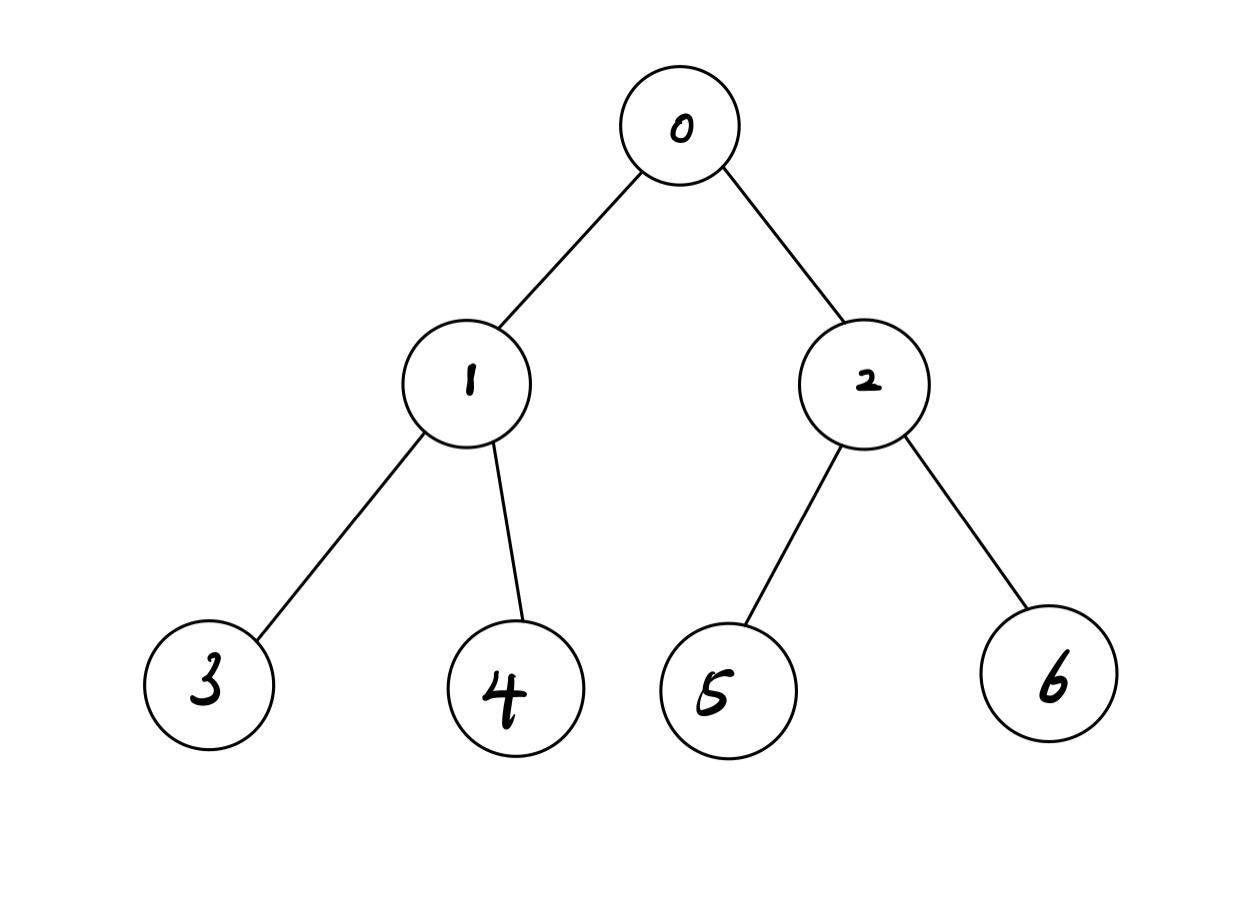
 把树的每层从左到右依次排序。

可以发现

左子节点 = 父节点 * 2 + 1；

右子节点 = 父节点 * 2 + 2；

填到数组中就是

 

    /**
     * 构造线段树
     * @param num   原数组
     * @param tree  这里的线段树其实是一个数组
     * @param node  树节点
     * @param start num的开始下标
     * @param end num的结束下标
     */
    private void buildTree(int[] num,int[] tree, int node, int start, int end){
        // 递归的出口
        // 每次将数组一分为二
        // 知道数组中就剩下一个数
        // 即start == end
        if (start == end){
            tree[node] = num[start];
        }else{
            int mid = (start+end)/2;
            // 根据父节点的下标求出子节点的下标
            int left_tree = node*2 + 1;
            int right_tree = 2*node + 2;
            // 递归调用
            buildTree(num,tree,left_tree,start,mid);
            buildTree(num, tree, right_tree, mid+1, end);
            // 父节点的值等于左右子节点值之和
            tree[node] = tree[left_tree]+tree[right_tree];
        }
    }

 

💕更新线段树

此时nums[3] = 6，如果我们要把nums[3]改为10，线段树要怎么修改呢？

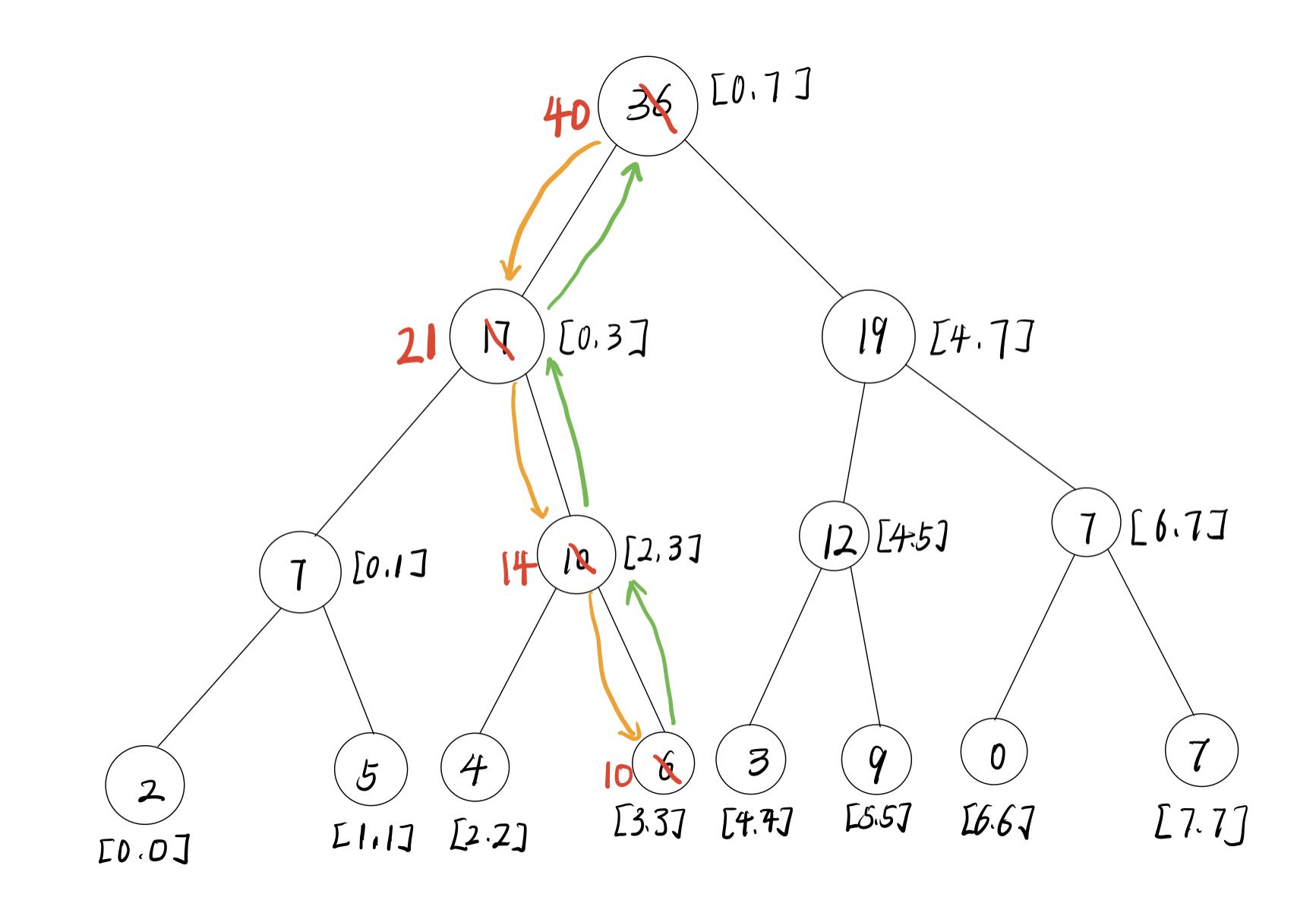
 先从父节点出发，找到nums[3]在线段树中对应的位置，修改节点后，在把沿途经过的父节点进行修改。

    /**
     * todo : 更新线段树
     * @param num
     * @param tree
     * @param node
     * @param start 开始的位置仍然为0 
     * @param end   结束的位置为nums的长度-1
     * @param index 要修改位置的下标
     * @param value 要修改的值
     */
    private void updateTree(int[] num,int[] tree, int node, int start, int end, int index, int value){
        if (start == end){
            num[index] = value;
            tree[node] = value;
        }else {
            int mid = (start + end) / 2;
            int left_tree = node * 2 + 1;
            int right_tree = node * 2 + 2;
            // 判断index在左右哪个区间里
            if (index >= start && index <= mid) {
                updateTree(num, tree, left_tree, start, mid, index, value);
            } else {
                updateTree(num, tree, right_tree, mid + 1, end, index, value);
            }
            // 修改沿途的父节点
            tree[node] = tree[left_tree]+tree[right_tree];
        }
    }

💕查找线段树

    /**
     * 查询线段树
     * @param nums
     * @param tree
     * @param node
     * @param start 开始的位置仍然为0
     * @param end   结束的位置仍然为nums的长度-1
     * @param L     nums[left]
     * @param R     nums[right]
     * @return
     */
    private int queryTree(int[] nums,int[] tree, int node, int start, int end, int L, int R){
        // 不在start 和 end的范围内
        if (R < start || L > end){
            return 0;
            // L 和 R包裹了start和end 所以直接返回该节点值即可
        }else if (L <= start && R >= end){
            return tree[node];
            // 单个节点的情况
        }else if (start == end){
            return tree[node];
        }else{
            int mid = (start + end) / 2;
            int left_tree = 2 * node + 1;
            int right_tree = 2 * node + 2;
            int sum_left = queryTree(nums, tree, left_tree, start, mid, L, R);
            int sum_right = queryTree(nums, tree, right_tree, mid+1, end, L, R);
            // 计算和
            return sum_left+sum_right;
        }
    }