对抗生成网络GAN系列——GANomaly原理及源码解析

Posted 2022-12-08 秃头小苏

🍊作者简介：秃头小苏，致力于用最通俗的语言描述问题

🍊往期回顾：对抗生成网络GAN系列——GAN原理及手写数字生成小案例   对抗生成网络GAN系列——DCGAN简介及人脸图像生成案例   对抗生成网络GAN系列——AnoGAN原理及缺陷检测实战   对抗生成网络GAN系列——EGBAD原理及缺陷检测实战

🍊近期目标：写好专栏的每一篇文章

🍊支持小苏：点赞👍🏼、收藏⭐、留言📩

 

文章目录

• 对抗生成网络GAN系列——GANomaly原理及源码解析
• • 写在前面
  • GANomaly原理解析
  • • GANomaly结构
    • GANomaly损失函数
    • GANomaly测试阶段
  • GANomaly源码解析
  • • GANomaly模型搭建
    • GANomaly损失函数
    • 小结
  • 参考链接

对抗生成网络GAN系列——GANomaly原理及源码解析

写在前面

​ 在前面，我已经介绍过好几篇有关GAN的文章，链接如下：

• [1]对抗生成网络GAN系列——GAN原理及手写数字生成小案例 🍁🍁🍁
• [2]对抗生成网络GAN系列——DCGAN简介及人脸图像生成案例🍁🍁🍁
• [3]对抗生成网络GAN系列——CycleGAN原理🍁🍁🍁
• [4] 对抗生成网络GAN系列——AnoGAN原理及缺陷检测实战 🍁🍁🍁
• [5]对抗生成网络GAN系列——EGBAD原理及缺陷检测实战🍁🍁🍁
• [6]对抗生成网络GAN系列——WGAN原理及实战演练🍁🍁🍁

  这篇文章我将来为大家介绍GANomaly，论文名为：Semi-Supervised Anomaly Detection via Adversarial Training。这篇文章同样是实现缺陷检测的，因此在阅读本文之前建议你对使用GAN网络实现缺陷检测有一定的了解，可以参考上文链接中的[4]和[5]。

  准备好了吗，嘟嘟嘟，开始发车。🚖🚖🚖

 

GANomaly原理解析

---

【阅读此部分前建议对GAN的原理及GAN在缺陷检测上的应用有所了解，详情点击写在前面中的链接查看，本篇文章我不会再介绍GAN的一些先验知识。】

---

GANomaly结构

​ 这部分为大家介绍GANomaly的原理，其实我们一起来看下图就足够了：

​

图1 GANomaly结构图

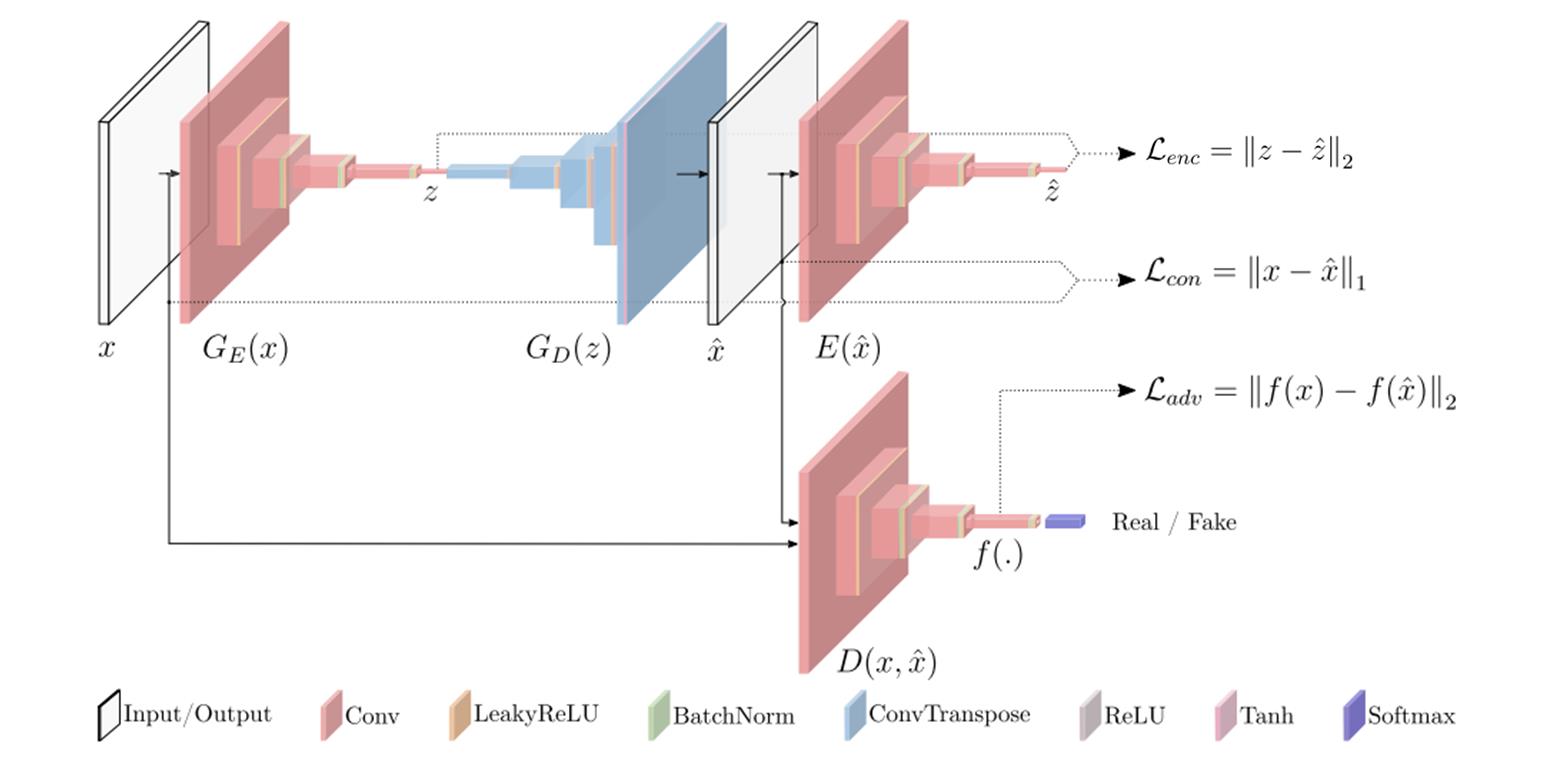
  我们还是先来对上图中的结构做一些解释。从直观的颜色上来看，我们可以分成两类，一类是红色的Encoder结构，一类是蓝色的Decoder结构。Encoder主要就是降维的作用啦，如将一张张图片数据压缩成一个个潜在向量；相反，Decoder就是升维的作用，如将一个个潜在向量重建成一张张图片。按照论文描述的结构来分，可以分成三个子结构，分别为生成器网络G，编码器网络E和判别器网络D。下面分别来介绍介绍这三个子结构：

• 生成器网络G
    生成器网络G由两个部分组成，分别为编码器$G_E(x))$和解码器$G_D(z)$，其实这就是一个自动编码器结构，主要用来学习输入x的数据分布并重建图像$\hat{x}$。我们一个个来看，先看$G_E(x)$结构，假设我们的输入x维度为${\mathbb{R}}^{C\times H\times W}$，经过$G_E(x)$结构后，变成一个向量$z$，其维度为${\mathbb{R}}^d$。【$G_E(x)$具体结构很简单啦，这里就不详细介绍了。我会在源码解析部分给出，大家肯定一看就会。】接着我们来看$G_D(z)$结构，它会将刚刚得到的向量z上采样成$\hat{x}$，$\hat{x}$的维度和$x$一致，都为${\mathbb{R}}^{C\times H\times W}$。关于$G_D(Z)$结构也很简单，其主要用到了转置卷积，对于转置卷积不了解的可以看博客[2]了解详情。生成器网络G就为大家介绍完了，是不是发现很简单呢。总结下来就两步，第一步让输入x通过$G_E(x)$得到z，第二步让z通过$G_D(Z)$变成$\hat{x}$。这两步也可以用一步表示，即$\hat{x}=G(x)$。

    思来想去我还是想在这里给大家抛出一个问题，我们传统的GAN是怎么通过生成器来构建假图像的呢？和GANomaly有区别吗？其实这个问题的答案很简单，大家都稍稍思考一下，我就不给答案了，不明白的评论区见吧！！！🥂🥂🥂

  ​

• 编码器网络E

  ​   编码器网络E的作用是将生成器得到的$\hat{x}$压缩成一个向量$\hat{z}$，是不是发现和生成器网络中的$G_E(x)$很像呢，其实呀，它俩的结构就是完全一样的，生成的$\hat{z}$ 和$\hat{x}$ 的维度一致，这是方便后面的损失比较。

 

• 判别器网络D

  ​   判别器网络D和我们之前介绍DCGAN时的结构是一样的，都是将真实数据$x$和生成数据$\hat{x}$输入网络，然后得出一个分数。

 

GANomaly损失函数

  GANomaly的损失函数分为两部分，第一部分是生成器损失，第二部分为判别器损失，下面我们分别来进行介绍：

• 生成器损失函数

  ​ 生成器损失函数又由三个部分组成，分别如下：

  • Adversari Loss

    我还是直接上公式吧，如下：

    ​ $$L_{adv}=E_{x\sim px}||f(x)-E_{x\sim px}f(G(x))|{|}_2$$

    这个公式对应图一中的$L_{adv}=||f(x)-f(\hat{x})|{|}_2$🍵🍵🍵这个损失函数应该很好理解，在前面介绍的GAN网络都有提及，$f(\ast )$表示判别器网络某个中间层的输出。这个损失函数的作用就是让两张图像$x和\hat{x}$尽可能接近，也就是让生成器生成的图片更加逼真。

    ---

  • Contextual Loss

    同样的，直接来上公式，如下：

    ​ $$L_{con}=E_{x\sim px}||x-G(x)|{|}_1$$

    这个公式对应图一中的$L_{con}=||x-\hat{x}|{|}_1$🍵🍵🍵这个函数其实也是要让两张图像$x和\hat{x}$尽可能接近。至于这里为什么用的是L1范数而不是L2范数，作者在论文中说这里使用L1范数的效果要比使用L2范数的效果好，这属于实验得到的结论，大家也不用过于纠结。

  • Encoder Loss

    话不多说，上公式，如下：

    ​ $$L_{enc}=E_{x\sim px}||G_E(x)-E(G(x))|{|}_2$$

    这个公式对应图一中的$L_{enc}=||z-\hat{z}|{|}_2$🍵🍵🍵这里的损失函数在我看来主要作用就是让我们在推理过程中的效果更好，这里就像AnoGAN中不断搜索最优的那个z的作用。

    ---

    如果大家这里读过cycleGAN的论文的话，可能会觉得这个损失函数有点类似cycleGAN中的循环一致性损失。我觉得这篇文章的思想可能借鉴了cycleGAN中的思想，感兴趣的可以去阅读一下，非常有意思的一篇文章！！！🥃🥃🥃

  ---

  ---

  生成器总的损失是上述三种损失的加权和，如下：
  $$对抗生成网络GAN系列——Spectral\; Normalization原理详解及源码解析$$

  GAN 系列的探索与pytorch实现 (数字对抗样本生成)

  [Pytorch系列-61]：生成对抗网络GAN - 基本原理 - 自动生成手写数字案例分析

  对抗生成网络GAN系列——DCGAN简介及人脸图像生成案例

  对抗生成网络GAN系列——CycleGAN简介及图片春冬变换案例

  [Pytorch系列-65]：生成对抗网络GAN - 图像生成开源项目pytorch-CycleGAN-and-pix2pix - 无监督图像生成CycleGan的基本原理