AVL树详解

Posted 2022-11-25 wanglelelihuanhuan

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了AVL树详解相关的知识，希望对你有一定的参考价值。

AVL树定义：

AVL树又称为高度平衡的二叉搜索树。它能保持二叉树的高度平衡，尽量降低二叉树的高度，减少树的平均搜索长度。

AVL树性质：

左子树和右子树的高度之差的绝对值不超过1
树中的每个左子树和右子树都是AVL树
每个节点都有一个平衡因子(balance factor--bf),任一节点的平衡因子是-1,0,1。(每个节点的平衡因子等于右子树的高度减去左子树的高度 )

AVL树效率：一棵AVL树有N个节点，其高度可以保持在lgN，插入/删除/查找的时间复杂度也是lgN。
AVL树节点信息如下：

template<class K, class V>
struct AVLTreeNode

	K _key;  //关键字
	V _value; 

	AVLTreeNode<K, V>* _parent;//父亲
	AVLTreeNode<K, V>* _left;//左孩子
	AVLTreeNode<K, V>* _right;//右孩子

	int _bf;//平衡因子
	AVLTreeNode<K, V>(const K& key, const V& value)//构造函数
		: _key(key)
		, _value(value)
		, _parent(NULL)
		, _left(NULL)
		, _right(NULL)
		, _bf(0)
	
;

AVL树操作包括：插入，查找，删除等。由于AVL树要求左右子树高度差的绝对值不超过1，因此AVL树必须通过旋转调平衡因子保持平衡。
插入：先插入节点再调平衡因子。

1、插入节点：

（1）若AVL树为空则new一个节点作为根节点；

（2）若要插入的节点等于根节点，返回false；

（3）若要插入的节点大于根节点，递归右子树插入节点，反之递归左子树插入节点。

2、调平衡因子（通过旋转）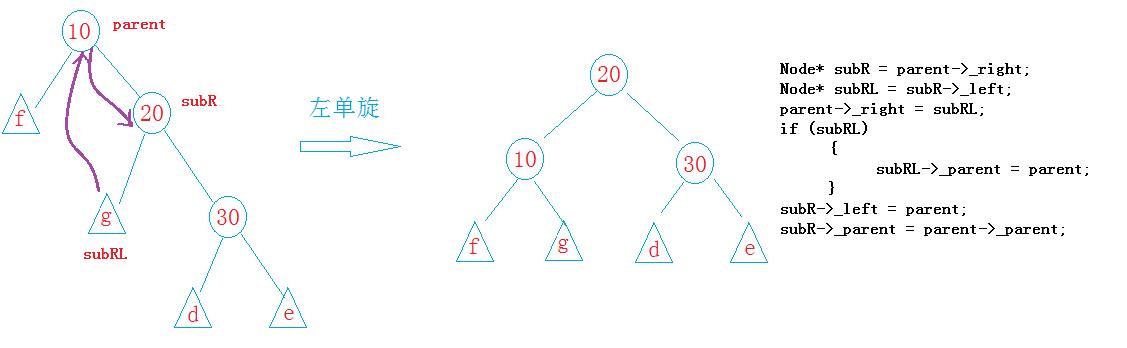

void _RotateL(Node*& parent)  // '\\'  ->   '/\\'
	
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;

		if (subRL)
		
			subRL->_parent = parent;
		

		subR->_left = parent;
		subR->_parent = parent->_parent;
		Node* ppNode = parent->_parent;
		parent->_parent = subR;
		//更新节点信息
		if (ppNode == NULL)
		
			_root = subR;
			subR->_parent = NULL;
		
		else if (ppNode->_left == parent)
		
			ppNode->_left = subR;
		
		else
		
			ppNode->_right = subR;
		
		subR->_parent = ppNode;
		parent->_bf = subR->_bf = 0;//更新平衡因子

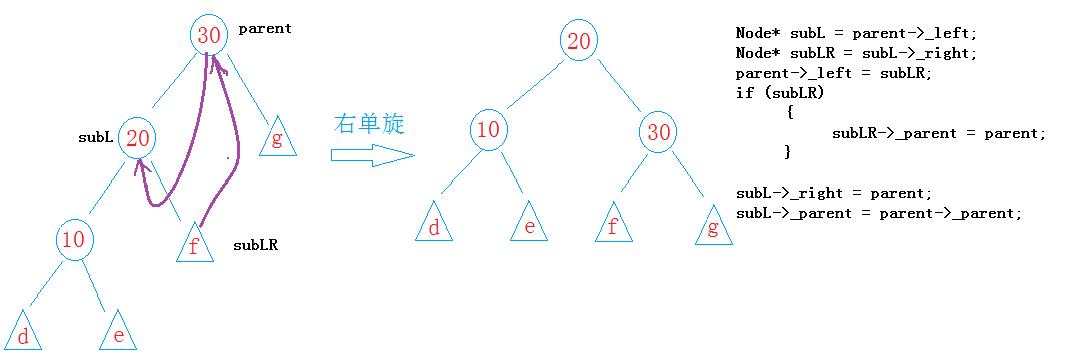
void _RotateR(Node*& parent)   // '/'  ->   '/\\'
	
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;

		if (subLR)
		
			subLR->_parent = parent;
		

		subL->_right = parent;
		subL->_parent = parent->_parent;
		Node* ppNode = parent->_parent;
		parent->_parent = subL;
		//更新节点信息
		if (ppNode == NULL)
		
			_root = subL;
			subL->_parent = NULL;
		
		else if (ppNode->_left == parent)
		
			ppNode->_left = subL;
		
		else
		
			ppNode->_right = subL;
		
		subL->_parent = ppNode;
		parent->_bf = subL->_bf = 0;//更新平衡因子

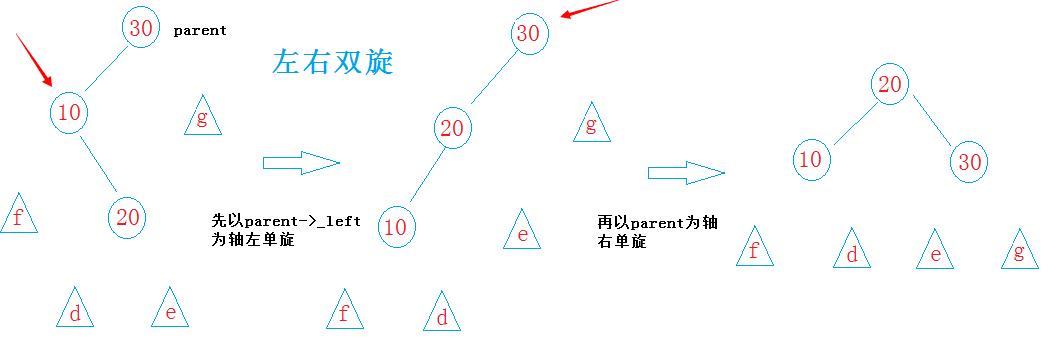
查找：

1、若搜索树为空则返回空；

2、若要查找的节点等于根节点，返回根节点；

3、若要查找的节点大于根节点，递归查找右子树，反之递归查找左子树。

Node* Find(const K& key)
	
		if (_root == NULL)
		
			return NULL;
		
		if (key > _root->_key)
		
			_root = _root->_right;
		
		else if (key < _root->_key)
		
			_root = _root->_left;
		
		else
		
			return _root;
		
		return NULL;

此外还有删除操作，先删除节点再调平衡因子。删除方法和搜索二叉树删除方法（http://blog.csdn.net/wanglelelihuanhuan/article/details/51585941）一样

完整代码如下：

AVLTree.h

#include<math.h>

template<class K, class V>
struct AVLTreeNode

	K _key;  //关键字
	V _value; 

	AVLTreeNode<K, V>* _parent;//父亲
	AVLTreeNode<K, V>* _left;//左孩子
	AVLTreeNode<K, V>* _right;//右孩子

	int _bf;//平衡因子
	AVLTreeNode<K, V>(const K& key, const V& value)//构造函数
		: _key(key)
		, _value(value)
		, _parent(NULL)
		, _left(NULL)
		, _right(NULL)
		, _bf(0)
	
;

template<class K, class V>
class AVLTree

	typedef AVLTreeNode<K, V> Node;
public:
	AVLTree()
		:_root(NULL)
	
	Node* Find(const K& key)
	
		if (_root == NULL)
		
			return NULL;
		
		if (key > _root->_key)
		
			_root = _root->_right;
		
		else if (key < _root->_key)
		
			_root = _root->_left;
		
		else
		
			return _root;
		
		return NULL;
	
	bool Insert(const K& key,const V& value)
	
		//先插入节点
		if (_root == NULL)
		
			_root = new Node(key, value);
			return true;
		
		Node* parent = NULL;
		Node* cur = _root;
		while (cur)
		
			if (key > cur->_key)
			
				parent = cur;
				cur = cur->_right;
			
			else if (key < cur->_key)
			
				parent = cur;
				cur = cur->_left;
			
			else
			
				return false;
			
		
		cur = new Node(key, value);
		if (key > parent->_key)
		
			parent->_right = cur;
			cur->_parent = parent;
		
		else
		
			parent->_left = cur;
			cur->_parent = parent;
		
		
		//再调平衡因子
		while (parent)
		
			if (parent->_left == cur)
			
				parent->_bf--;
			
			else
			
				parent->_bf++;
			

			if (parent->_bf == 0)  //已经是平衡树
			
				break;
			
			else if (parent->_bf == -1 || parent->_bf == 1) //继续回溯
			
				cur = parent;
				parent = cur->_parent;
			
			else // -2  2  调整 旋转
			
				if (parent->_bf == 2)
				
					if (cur->_bf == 1)  //  '\\'   左单旋  
					
						_RotateL(parent);
					
					else  //-1   '>' 右左双旋
					
						_RotateRL(parent);
					
				
				else  //-2
				
					if (cur->_bf == -1)  // '/' 右单旋
					
						_RotateR(parent);
					
					else   // '<' 左右双旋
					
						_RotateLR(parent);
					
				
				break;
			
		
		return true;
	
	void Inorder()
	
		_Inorder(_root);
		cout << endl;
	

	bool IsBalance()
	
		return _IsBalance(_root);
	
protected:
	void _RotateL(Node*& parent)  // '\\'  ->   '/\\'
	
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;

		if (subRL)
		
			subRL->_parent = parent;
		

		subR->_left = parent;
		subR->_parent = parent->_parent;
		Node* ppNode = parent->_parent;
		parent->_parent = subR;
		//更新节点信息
		if (ppNode == NULL)
		
			_root = subR;
			subR->_parent = NULL;
		
		else if (ppNode->_left == parent)
		
			ppNode->_left = subR;
		
		else
		
			ppNode->_right = subR;
		
		subR->_parent = ppNode;
		parent->_bf = subR->_bf = 0;//更新平衡因子
	
	void _RotateR(Node*& parent)   // '/'  ->   '/\\'
	
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;

		if (subLR)
		
			subLR->_parent = parent;
		

		subL->_right = parent;
		subL->_parent = parent->_parent;
		Node* ppNode = parent->_parent;
		parent->_parent = subL;
		//更新节点信息
		if (ppNode == NULL)
		
			_root = subL;
			subL->_parent = NULL;
		
		else if (ppNode->_left == parent)
		
			ppNode->_left = subL;
		
		else
		
			ppNode->_right = subL;
		
		subL->_parent = ppNode;
		parent->_bf = subL->_bf = 0;//更新平衡因子
	
	void _RotateLR(Node*& parent)   //  '<'  ->   '/'  ->   '/\\'
	
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		_RotateL(parent->_left);
		_RotateR(parent);

		if (bf == 1)
		
			subL->_bf = -1;
			parent->_bf = 0;
		
		else if (bf == -1)
		
			subL->_bf = 0;
			parent->_bf = 1;
		
		else
		
			subL->_bf = parent->_bf = 0;
		
		subLR->_bf = 0;
		
	
	void _RotateRL(Node*& parent)
	
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		
		int bf = subRL->_bf;
		_RotateR(parent->_right);
		_RotateL(parent);
		if (bf == 1)
		
			subR->_bf = 0;
			parent->_bf = -1;
		
		else if (bf == -1)
		
			subR->_bf = 1;
			parent->_bf = 0;
		
		else
		
			subR->_bf = parent->_bf = 0;
		
		subRL->_bf = 0;
	
	int _Height(Node* root)
	
		if (root == NULL)
		
			return 0;
		
		int Left = _Height(root->_left);
		int Right = _Height(root->_right);
		return (Left > Right ?  Left:Right)+1;
	
	void _Inorder(Node* root)
	
		if (root == NULL)
			return ;

		_Inorder(root->_left);
		cout << root->_key << " ";
		_Inorder(root->_right);
	
	bool _IsBalance(Node*& root)
	
		if (root == NULL)
		
			return true;
		
		int bf = _Height(root->_right) - _Height(root->_left) ;
		if (abs(bf) > 1 || bf != root->_bf)
		
			cout << "平衡因子有问题：" << root->_key << endl;
			return false;
		
		return _IsBalance(root->_left) && _IsBalance(root->_right);
	
protected:
	Node* _root;
;

void TestInsert()

	int arr1[] =  16, 3, 7, 11, 9, 26, 18, 14, 15 ;
	AVLTree<int, int> alt1;
	for (int i = 0; i < sizeof(arr1) / sizeof(arr1[0]); ++i)
	
		alt1.Insert(arr1[i],i);
	
	alt1.Inorder();
	cout << "isBlance? " << alt1.IsBalance() << endl;


	int arr[] =  4, 2, 6, 1, 3, 5, 15, 7, 16,14;
	AVLTree<int, int> alt2;
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); ++i)
	
		alt2.Insert(arr[i], i);
	
	alt2.Inorder();
	
	cout << "isBlance? " << alt2.IsBalance() << endl;

Test.cpp

#include<iostream>
using namespace std;

#include"AVLTree.h"

int main()

	TestInsert();
	return 0;

以上是关于AVL树详解的主要内容，如果未能解决你的问题，请参考以下文章

AVL树平衡旋转详解

[C/C++]详解STL容器6--AVL树的介绍及部分模拟实现

[C/C++]详解STL容器4--AVL树的介绍及部分模拟实现

[C/C++]详解STL容器6--AVL树的介绍及部分模拟实现

数据结构 - 从二叉搜索树说到AVL树之二叉搜索树的操作与详解（Java）

平衡树AVL树