机器学习基本算法总结

Posted 2022-11-09 Maggie张张

写这篇博文主要是想对自己近期学到的机器学习知识做一个总结，同时也谈一谈我对人工智能的理解。

一、我对人工智能的理解

首先谈一谈我对人工智能的理解。人工智能企图理解智能的本质，并让机器也拥有类似于人的智能。比如，人从出生到慢慢长大，能听懂别人的话，能辨认周围的物体，并且能模仿一些举动，所以人是拥有智能的。但是机器不行，一开始机器可以完成一些人类已经明确告诉它怎么去完成的任务（比如人编写程序告诉计算机加法的逻辑是什么，计算机就可以完成加法的计算），但是一些需要推断的任务机器就没法做到了，而机器学习就是让机器有学习的能力，从而拥有智能的方法。
人有学习的能力，是从大量接收到的讯息中总结出了某种规律，从而能对陌生的物体作出推断。那么，机器想要拥有像人一样的学习能力，首先就要给他大量的输入讯息，其次根据不同的目的就需要通过不同的方法（机器学习算法）来总结出一个模型，然后可以利用这个模型对未知事例作出判断。
机器学习的应用领域现在已经渗透到了很多方面，比如文字识别、图像识别、垃圾邮件分类、股票预测等等。
机器学习的方式，大致可以分为监督学习、无监督学习、半监督学习等等，区别就在于是否给出了样本的标签。
所谓监督学习，就是学习的过程要不断的用样本的标签信息来校正你的学习结果。
根据样本标签是离散值还是连续值，监督学习可以分成分类和回归。典型的算法有单层感知机、K近邻、朴素贝叶斯、支持向量机、神经网络等等，Logistic回归、线性回归等等。
无监督学习，就是学习的过程不需要样本的标签信息，仅仅通过样本自身的特征来得到一些知识。
比如K-聚类，就是根据样本间的欧氏距离的远近来对样本进行一个划分，在比如关联规则挖掘，就是从大量数据找出某些规则。这些算法的过程都是不需要样本的类别信息的。

二、基本的机器学习算法总结

这里，我只简单的总结下列算法：

分类算法: 单层感知机、神经网络的反向传播算法、Logistic回归、朴素贝叶斯、K近邻、SVM、集成学习

聚类算法: k-means、二分k-means、DBSCAN

单层感知机

   单层感知机旨在从训练数据集中得到一个线性的分类超平面，学习的策略是使所有误分类样本距离超平面的距离最小，具体采用随机梯度下降法，每次随机找到一个误分类样本，使这个样本沿着最小化目标函数的方向更新参数。
给定一个训练数据集

$$T=\\left \\ \\left ( x_1,y_1 \\right ), \\left ( x_2,y_2 \\right ),...,\\left ( x_N,y_N \\right )\\right \\$$
其中 $x\\in X=\\mathbbR^n, y_i\\in Y=\\left\\-1,1\\right\\, i=1,2,...,N$, 因为误分类样本 $y_i(w_i\\ast x_i+b)$小于零，所以目标函数是
$$minL\\left ( w,b \\right )=-\\sum_x_i\\in My_i(w_i\\ast x_i+b)$$
得到的感知机模型就是一个由w, b决定的超平面，
$$f(x)=sign\\left ( w*x+b \\right )$$

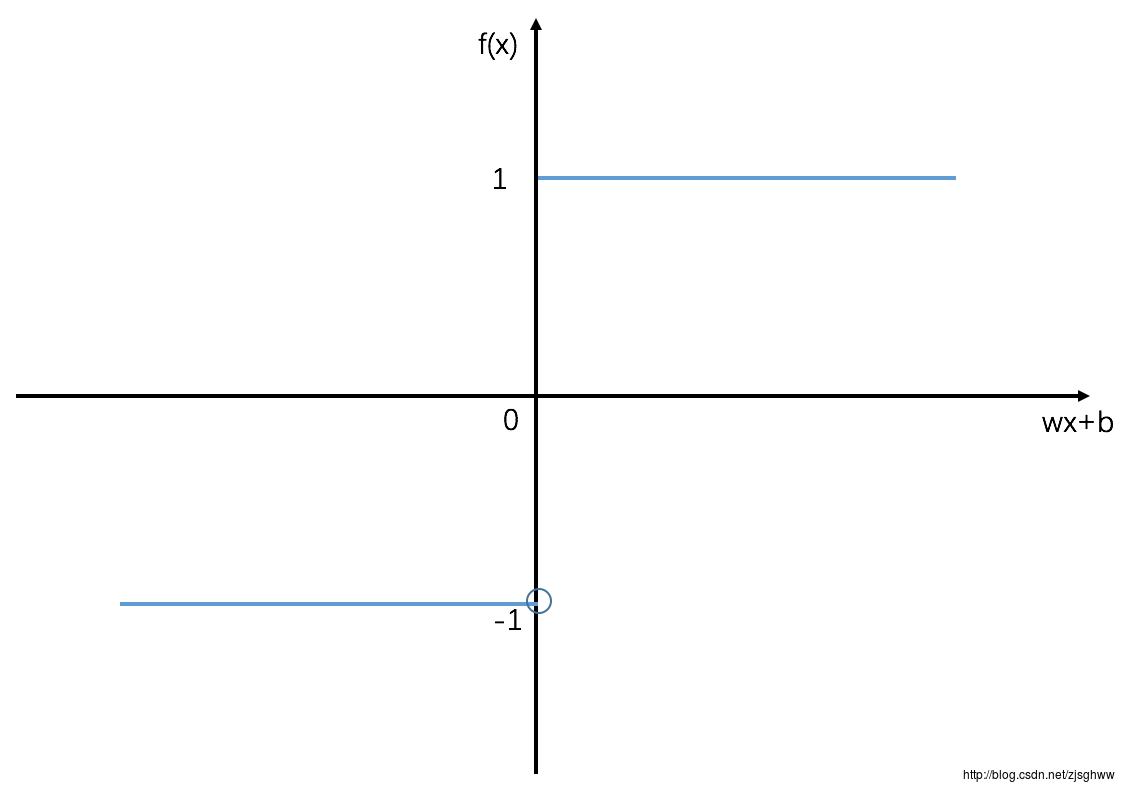
神经网络-前向后向传播算法

  单层感知机很简单，只能解决线性可分的问题，对于线性不可分的情况可能会产生震荡，参数w,b的取值无法收敛。那么，全联接神经网络就是将多个感知机结合在了一起，变成了一个层状结构的有向图。除了输入层和输出层以外还有隐层，从而可以解决线性不可分的情况。

在神经网络中，每一个功能单元（即除了输入层的单元以外的神经元）都有自己的一组参数（w、b），可以将自己的输入进行线性组合后得到一个状态值，然后经过Sigmoid函数将状态值变换成激活值，接着将这个激活值作为下一层单元的输入，直到最终得到输出层的结果，这就是前向传播算法。神经网络的模型就是由这些一组组的（w、b）参数组成的，训练模型的过程就是找出能最好地拟合训练样本的特点的参数。反向误差传播算法（Back Propagation）就是训练参数（w、b）的。
反向传播算法的基本思想是：
（1）先初始化所有的参数w、b，根据前向传播算法计算每一层的状态值和激活值
（2）计算每一层的误差，误差的计算是从后向前推进的
（3）更新参数（目标是让误差变小）
（4）迭代2，3步骤，知道满足停止条件

假设单个样本的误差是E，$E=\\frac12\\left \\| (y-o) \\right \\|$, 其中y是样本的理应输出，o是计算得到的结果。我们的目标是让所有样本的误差最小，那么只需要让每一个样本的误差最小即可获得整体最小。BP采用批量梯度下降法更新参数。

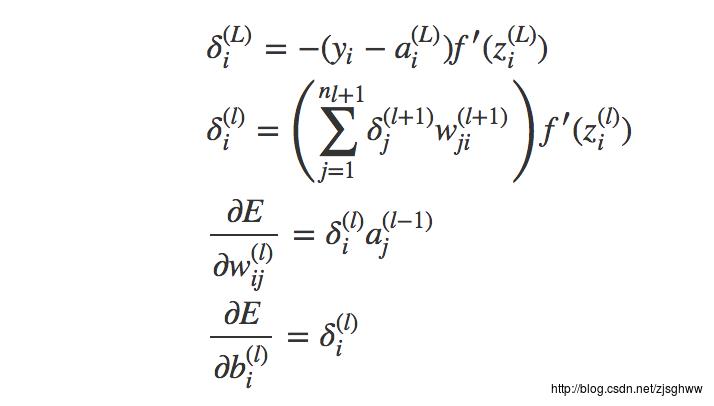
每一层传播的误差就是$\\sigma^\\left ( l \\right )$，每个功能单元都会有自己的误差$\\sigma^\\left ( l \\right )_i$，因为它有自己的参数w, b，这样在一次迭代中，每个单元都可以根据误差计算到参数梯度下降的值$\\frac\\partial E\\partial w_ij^(l))$和$\\frac\\partial E\\partial b_i^(l))$

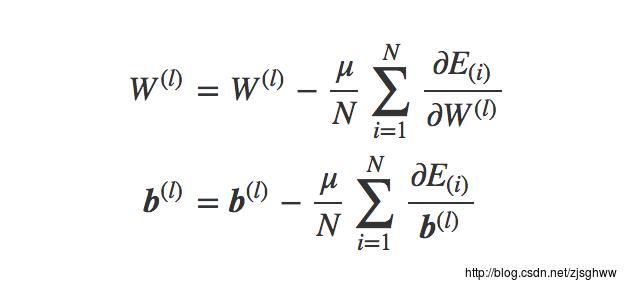
将所有样本在各个单元参数梯度下降的值求平均就可以完成一次参数的更新——批量梯度下降法。

所以说，神经网络的学习策略是靠误差驱动的。

Logistic回归

   Logistic回归可以类比于单层感知机，两者都想从样本中学习到参数w、b，从而得到一个分类超平面，只不过前者是把输入经过参数作用后的结果用Sigmoid函数转换成了（0，1）之间的值，然后把这个值看成了一个属于某一类的概率，用极大似然估计来求解满足条件时使得概率最大化时的参数，而后者从误分类样本的性质考虑来优化参数。
似然函数

$$L\\left ( \\theta \\right )=\\prod_i=1^NP(y_i|x_i;\\theta)=\\prod_i=1^Nh_\\theta^y_i(1-h_\\theta)^1-y_i$$
对似然函数取对数，求偏导，然后用批量梯度下降求解参数 $\\theta$ (即w,b)
但是，单层感知机和Logistic回归只能在数据线性可分或者近似线性可分的情况下才能学习到比较好的参数，面对数据线性不可分的情况就效果不太好了。

支持向量机（SVM）

   支持向量机可以通过核技巧将特征变换到高维空间，从而将低维空间线性不可分的情况在高维空间变得线性可分。
   支持向量机的基础仍然是单层感知机，从一堆样本 (xi,以上是关于机器学习基本算法总结的主要内容，如果未能解决你的问题，请参考以下文章

机器学习基本算法总结

机器学习基本算法总结

机器学习的9个基础概念和10种基本算法总结

《统计学习》——感知机

机器学习预测算法有问题

机器学习-聚类算法2