理解快速离散傅里叶变换算法(FFT)
Posted Jie Qiao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了理解快速离散傅里叶变换算法(FFT)相关的知识,希望对你有一定的参考价值。
本文是视频The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?的整理。
离散傅里叶变换的用法
FFT是一个非常快速的离散傅里叶变换算法,他的算法复杂度是 O ( n log n ) \\displaystyle O( n\\log n) O(nlogn)。在讲解FFT之前,我们先介绍普通的离散傅里叶变换的的输入和输出是什么?以及一个离散傅里叶变换的简单应用。离散傅里叶变换的输入是一个数组,比如[5,3,2,1],输出是对应的复数,[11,3-2i,3,3+2i],可以自己试试:
from numpy.fft import fft
fft([5,3,2,1])
这个5,3,2,1可以看做是一个多项式的系数:
P ( x ) = 5 + 3 x + 2 x 2 + x 3 P( x) =5+3x+2x^2 +x^3 P(x)=5+3x+2x2+x3
而这个对应的复数其实是这个多项式的在点 P ( w 0 ) , P ( w 1 ) , P ( w 2 ) , P ( w 3 ) \\displaystyle P\\left( w^0\\right) ,P\\left( w^1\\right) ,P\\left( w^2\\right) ,P\\left( w^3\\right) P(w0),P(w1),P(w2),P(w3)的值,其中 w = e 2 π i / n \\displaystyle w=e^2\\pi i/n w=e2πi/n,这里 n = 4 \\displaystyle n=4 n=4。之所以 w \\displaystyle w w要设置成这个值是因为复数有个神奇的周期性:
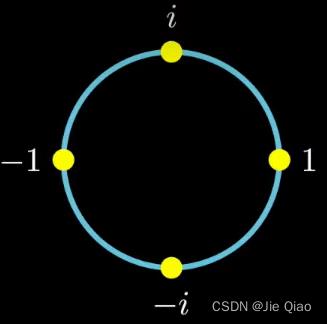
对应着, w 0 = 1 , w 1 = e 2 π i / 4 = i , w 2 = e 4 π i / 4 = − 1 , w 3 = e 8 π i / 4 = − i \\displaystyle w^0 =1,w^1 =e^2\\pi i/4 =i,w^2 =e^4\\pi i/4 =-1,w^3 =e^8\\pi i/4 =-i w0=1,w1=e2πi/4=i,w2=e4πi/4=−1,w3=e8πi/4=−i,可以发现他相当于从1开始,在这个单位元上平均取了4个点,而且这4个点正是多项式 x 4 = 1 \\displaystyle x^4 =1 x4=1的根。可以看下面这个视频,里面也介绍了复数的这种周期性的性质:

我们把这四个点代进方程
P ( w 0 ) = 5 + 3 + 2 + 1 = P ( 1 ) = 11 P ( w 1 ) = 5 + 3 ω + 2 ω 2 + ω 3 = P ( i ) = 3 + 2 i P ( w 2 ) = 5 + 3 ω 2 + 2 ω 4 + ω 6 = P ( − 1 ) = 3 P ( w 3 ) = 5 + 3 ω 3 + 2 ω 6 + ω 12 = P ( − i ) = 3 − 2 i \\beginaligned P\\left( w^0\\right) & =5+3+2+1=P( 1) =11\\\\ P\\left( w^1\\right) & =5+3\\omega +2\\omega ^2 +\\omega ^3 =P( i) =3+2i\\\\ P\\left( w^2\\right) & =5+3\\omega ^2 +2\\omega ^4 +\\omega ^6 =P( -1) =3\\\\ P\\left( w^3\\right) & =5+3\\omega ^3 +2\\omega ^6 +\\omega ^12 =P( -i) =3-2i \\endaligned P(w0)P(w1)P(w2)P(w3)=5+3+2+1=P(1)=11=5+3ω+2ω2+ω3=P(i)=3+2i=5+3ω2+2ω4+ω6=P(−1)=3=5+3ω3+2ω6+ω12=P(−i)=3−2i
写成矩阵的形式就是:
[
P
(
ω
0
)
P
(
ω
1
)
P
(
ω
2
)
P
(
ω
3
)
]
=
[
1
1
1
1
1
ω
ω
2
ω
3
1
ω
2
ω
4
ω
8
1
ω
3
ω
6
ω
12
]
[
5
3
2
1
]
(1)
\\left[\\beginarray c P\\left( \\omega ^0\\right)\\\\ P\\left( \\omega ^1\\right)\\\\ P\\left( \\omega ^2\\right)\\\\ P\\left( \\omega ^3\\right) \\endarray\\right] =\\left[\\beginarray c c c c 1 & 1 & 1 & 1\\\\ 1 & \\omega & \\omega ^2 & \\omega ^3\\\\ 1 & \\omega ^2 & \\omega ^4 & \\omega ^8\\\\ 1 & \\omega ^3 & \\omega ^6 & \\omega ^12 \\endarray\\right]\\left[\\beginarray c 5\\\\ 3\\\\ 2\\\\ 1 \\endarray\\right]\\tag1
⎣
⎡P(ω0)P(ω1)P(ω2)P(ω3)⎦
⎤=⎣
⎡11111ωω2ω31ω2ω4ω61ω3ω8ω12⎦