快速傅里叶变换FFT及其延伸(只是一个引导)
Posted 出尘呢
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了快速傅里叶变换FFT及其延伸(只是一个引导)相关的知识,希望对你有一定的参考价值。
快速傅里叶变换FFT及其延伸
以下都是学习过程中,最终结果请看这:
http://book.baige.me/view/WlQ
呕心沥血爱傅里叶qwq
步骤
- 通过蓝书初步了解FFT
- 通过bloghttps://blog.csdn.net/enjoy_pascal/article/details/81478582/看懂FFT和NTT
(%*10000——博主是初二写的oi健er!) - 通过《算法导论》系统学习FFT和高效FFT
- 有所超越:(主要通过论文)学习FFT改进算法与非整数的FFT算法,可能有所新发现
步骤1. 通过蓝书初步了解FFT
《训练指南》p428《快速傅里叶变换FFT》
介绍
快速傅里叶变换是一个很有工程价值的算法,广泛应用于音频、图像等数字信号处理领域。傅里叶变换本身的理论很深。
概念
FFT(fast Fourier transform)是用来计算离散傅里叶变换(discrete Fourier transform,DFT)及其逆变换(IDFT)的快速算法。
直观理解
DFT把时域信号变换为频域信号。
例如声音信号,时域指音量大小,频域指音调高低。
在录音的时候,音频通常按时域形式保存,即各个时刻采样到的振幅;如果需要各个频率的数据,则需要DFT。
重要性质
时域卷积,频域卷积;频域卷积,时域卷积。
举例:快速多项式乘法
多项式乘法实际上是多项式系数向量的卷积。
问题:
给定两单变量多项式 A(x) 和 B(x) 次数均不超过 n ,如何快速计算两者乘积?
朴素的方法
系数两两相乘,再相加。
时间复杂度 O ( n2 )
慢!
快速的方法
优化方法
点值表示法表示多项式,相当于描点作图法。
只要两多项式点集相同,则把对应值乘起来就可以了。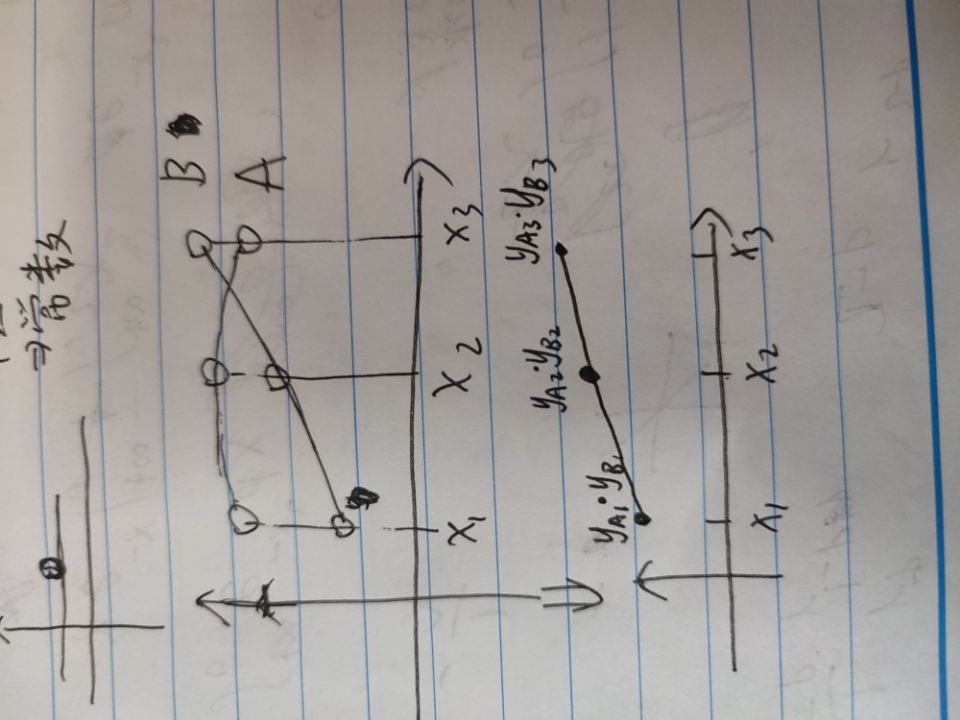
数形结合的思想。
这步的时间复杂度是 O ( n ) ,快。
定理: 恰好有一个次数小于n 的多项式满足拟合n 个离散的点。
(画图可看出,不知为何,,,横着了qwq)
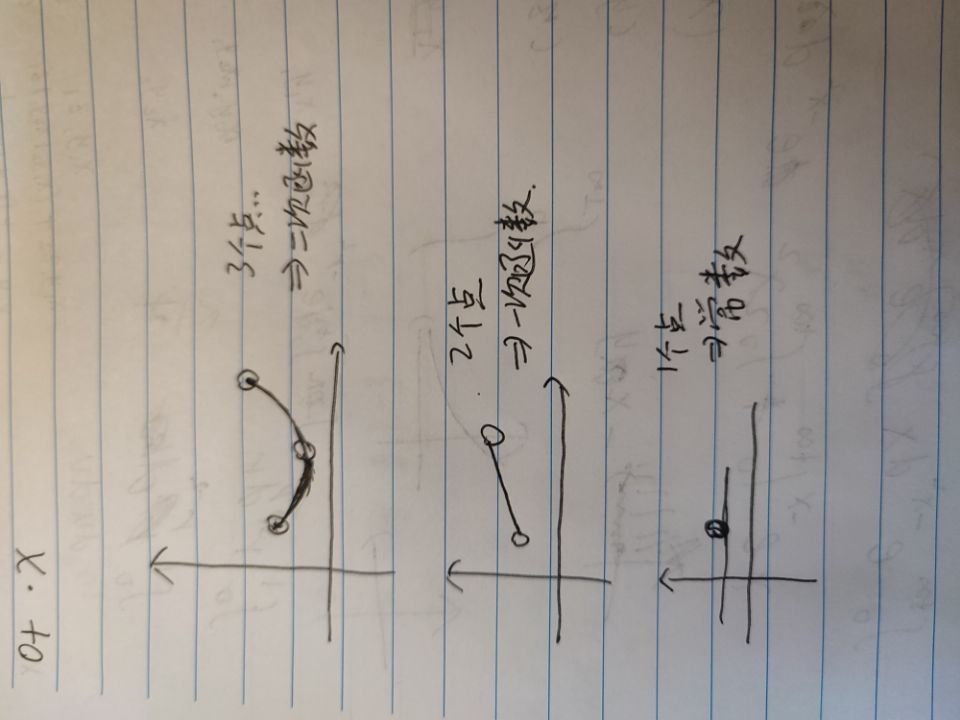
现在的问题是,通常输入输出的多项式都是系数表示的,
要进行傅里叶变换以换为点集表示。
快速傅里叶变换部分
系数表示对应于时域,点值表示对应于频域。
DFT:系数表示->点值表示。
IDFT:系数表示<-点值表示。
这样算出来的点值表示法,对应的求值点是2*n次单位根(暂时不加证明)
x = e k π i / n x=e^k\\pi i/n x=ekπi/n
证明如下:
单位根
n次单位根,
即满足
x
n
=
1
x^n=1
xn=1的复数。
欧拉复数公式:
e
i
x
=
c
o
s
x
+
i
∗
s
i
n
x
e^ix=cosx+i*sinx
eix=cosx+i∗sinx
泰勒展开式无穷级数,代入 i*x 即可。

对于
x
n
=
1
=
1
+
i
∗
0
x^n=1=1+i*0
xn=1=1+i∗0
由欧拉复数公式
c
o
s
(
u
)
=
1
cos(u)=1
cos(u)=1
s
i
n
(
u
)
=
0
sin(u)=0
sin(u)=0
则
u
=
2
k
π
u=2k\\pi
u=2kπ
代入有
x
=
e
2
k
π
i
/
n
x=e^2k\\pi i/n
x=e2kπi/n
快速多项式乘法具体步骤
- 补0
- 求值DFT
- 乘法
- 插值IDFT
——然而蓝书上说自己去找FFT详细过程。
“对应的求值点是2*n次单位根”也还需要证明。
步骤2. 通过blog看懂FFT和NTT
https://blog.csdn.net/enjoy_pascal/article/details/81478582/
(%*10000——博主是初二写的oi健er)
DFT前置知识&技能
复数
对
z
1
=
a
+
b
i
,
z
2
=
c
+
d
i
z_1=a+bi,z_2=c+di
z1=a+bi,z2=c+di
可看成
x
O
y
xOy
xOy坐标系的向量
有坐标表示形式
z
1
=
(
a
,
b
)
,
z
2
=
(
c
,
d
)
z_1=(a,b),z_2=(c,d)
z1=(a,b),z2=(c,d)
有优美的结论
z
1
+
z
2
=
(
a
+
b
,
c
+
d
)
z_1+z_2=(a+b,c+d)
z1+z2=(a+b,c+d)
极坐标表示形式
z
1
=
(
ρ
1
,
θ
1
)
,
z
2
=
(
ρ
2
,
θ
2
)
z_1=( \\rho1 ,\\theta1),z_2=(\\rho2,\\theta2)
z1=(ρ1,θ1),z2=(ρ2,θ2)
有优美的结论
z
1
∗
z
2
=
(
ρ
1
∗
ρ
2
,
θ
1
+
θ
2
)
z_1*z_2=(\\rho1*\\rho2,\\theta1+\\theta2)
z1∗z2=(ρ1∗ρ2,θ1+θ2)
- 证明
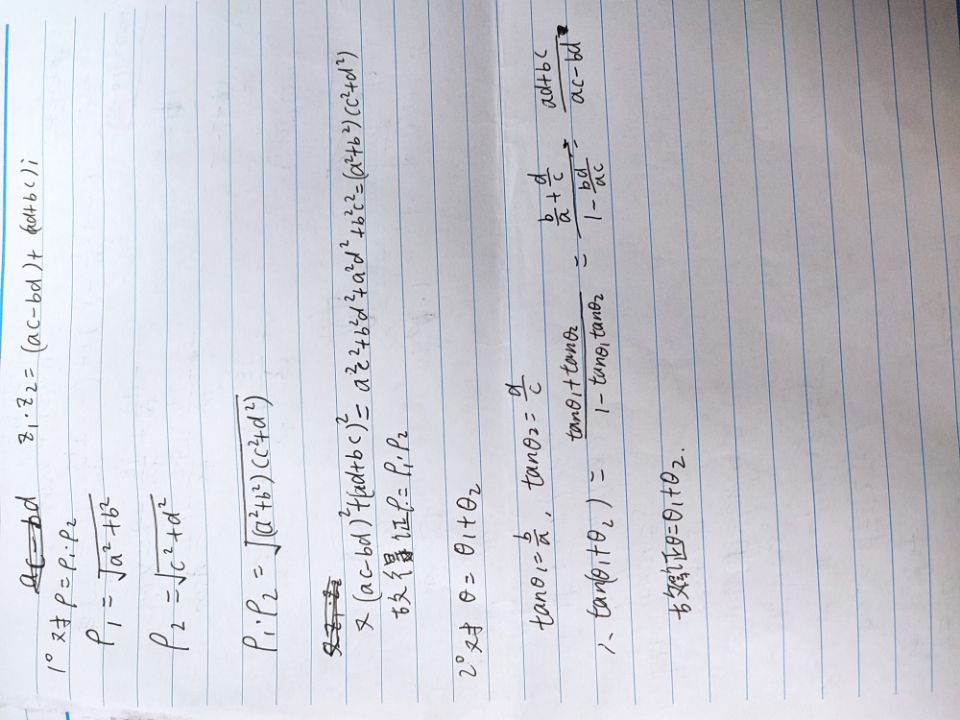
DFT(离散傅里叶变换)
- 一定注意从这里开始所有的
n
n
n都默认为
2
2
2的整数次幂
…
之后晚上在床上看算法导论觉得算法导论更清楚,所以步骤二无疾而终。。。
步骤3.通过《算法导论》系统学习FFT和高效FFT
这个,,,我应该不会比算法导论》讲的更好了
步骤4.一些改进的方向
NTT
https://horizonwd.blog.csdn.net/article/details/81771910
没有精度差
——blog路人黑的纸巾
从数值稳定性的角度,插值是一个众所周知的棘手问题。
——算法导论
变基FFT
什么意思呢
就是现在的FFT迭代是
a
=
a
1
+
x
∗
a
2
a=a_1+x*a_2
a=a1+x∗a2
因为是二因式,叫2基
拆分成
a
=
a
1
+
x
∗
a
2
+
x
2
∗
a
3
+
x
4
∗
a
4
a=a_1+x*a_2+x^2*a_3+x^4*a_4
a=a1+x∗a2+x2∗a3+x4∗a4
就是4基
例如,次数为16,
2基要
l
o
g
2
16
=
4
log_2 16=4
log216=4层
4基只要
l
o
g
4
16
=
2
log_4 16=2
log416=2层
多维FFT
多维在信息处理中有着更广泛的作用
若各维的维数为
n
1
,
n
2
,
.
.
.
,
n
k
n_1,n_2,...,n_k
n1,n2,...,nk
则令
n
=
n
1
,
n
2
,
.
.
.
,
n
k
n=n_1,n_2,...,n_k
n=n1,n2,...,nk
可以在
O
(
n
l
o
g
2
n
)
O(n log_2n)
O(nlog2n)时间复杂度内变换出
以上是关于快速傅里叶变换FFT及其延伸(只是一个引导)的主要内容,如果未能解决你的问题,请参考以下文章