数学篇05 # 如何用向量和坐标系描述点和线段？

Posted 凯小默

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数学篇05 # 如何用向量和坐标系描述点和线段？相关的知识，希望对你有一定的参考价值。

说明

【跟月影学可视化】学习笔记。

坐标系与坐标映射

  • html：采用的是窗口坐标系，以参考对象（参考对象通常是最接近图形元素的 position 非 static 的元素）的元素盒子左上角为坐标原点，x 轴向右，y 轴向下，坐标值对应像素值。
  • SVG：采用的是视区盒子（viewBox）坐标系。这个坐标系在默认情况下，是以 svg 根元素左上角为坐标原点，x 轴向右，y 轴向下，svg 根元素右下角坐标为它的像素宽高值。如果我们设置了 viewBox 属性，那么 svg 根元素左上角为 viewBox 的前两个值，右下角为 viewBox 的后两个值。
  • Canvas：采用的坐标系默认以画布左上角为坐标原点，右下角坐标值为 Canvas 的画布宽高值。
  • WebGL：是一个三维坐标系。它默认以画布正中间为坐标原点，x 轴朝右，y 轴朝上，z 轴朝外，x 轴、y 轴在画布中范围是 -1 到 1。

上面4个都属于直角坐标系。

直角坐标系特性：不管原点和轴的方向怎么变，用同样的方法绘制几何图形，它们的形状和相对位置都不变。

转换坐标系：

  • HTML、SVG 和 Canvas 都提供了 transform 的 API 转换坐标系。
  • WebGL 本身不提供 tranform 的 API，但可以在 shader 里做矩阵运算来实现坐标转换。

如何用 Canvas 实现坐标系转换？

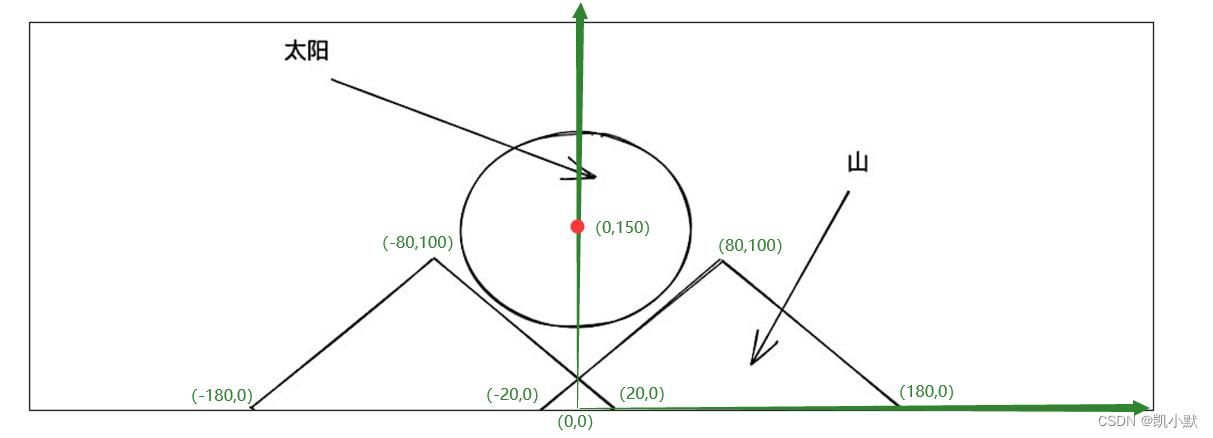
以一个例子为例：在宽 512 * 高 256 的一个 Canvas 画布上实现如下的视觉效果。其中，山的高度是 100，底边 200，山是等腰三角形，两座山的中心位置到中线的距离都是 80，太阳的圆心高度是 150。可以使用一个 Rough.js：https://github.com/rough-stuff/rough的库，绘制一个手绘风格的图像。

方法一：不转换坐标系

首先我们需要计算出来三角形各个顶点的坐标

然后绘制

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>不转换坐标系</title>
    <style>
        canvas 
            border: 1px dashed salmon;
        
    </style>
</head>
<body>
    <canvas width="512" height="256"></canvas>
    <script src="https://lib.baomitu.com/rough.js/3.1.0/rough.umd.js"></script>
    <script>
        const rc = rough.canvas(document.querySelector('canvas'));
        const hillOpts = 
            roughness: 2.8,
            strokeWidth: 2,
            fill: 'cyan'
        ;
        rc.path('M76 256 L176 156 L276 256', hillOpts);
        rc.path('M236 256 L336 156 L436 256', hillOpts);
        rc.circle(256, 106, 105, 
            stroke: 'red',
            strokeWidth: 4,
            fill: 'salmon',
            fillStyle: 'solid',
        );
    </script>
</body>
</html>

效果如下：

方法二：转换坐标系

以画布底边中点为原点，x 轴向右，y 轴向上的坐标系，相对来说转换之后的坐标系计算的坐标点简单清晰一些：

// 以画布底边中点为原点
ctx.translate(256, 256);
// x 轴向右，y 轴向上的坐标系
ctx.scale(1, -1);


<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>转换坐标系</title>
    <style>
        canvas 
            border: 1px dashed salmon;
        
    </style>
</head>
<body>
    <canvas width="512" height="512"></canvas>
    <script src="https://lib.baomitu.com/rough.js/3.1.0/rough.umd.js"></script>
    <script>
        const rc = rough.canvas(document.querySelector('canvas'));
        console.log(rc)
        const ctx = rc.ctx;
        // 以画布底边中点为原点
        ctx.translate(256, 256);
        // x 轴向右，y 轴向上的坐标系
        ctx.scale(1, -1);
        const hillOpts = 
            roughness: 2.8,
            strokeWidth: 2,
            fill: 'gray'
        ;
        // //线条宽度
        // ctx.lineWidth = 2;
        // ctx.fillStyle = 'orange';
        // //线条颜色填充
        // ctx.strokeStyle = 'black';
        // //开启绘画路径
        // ctx.beginPath();
        // //画笔初始化点
        // ctx.moveTo(-180, 0);
        // // 画笔目标位置
        // ctx.lineTo(-80, 100);
        // // 连接路径
        // ctx.stroke();
        // ctx.lineTo(20, 0);
        // ctx.stroke();
        // ctx.closePath(); //闭合线路(首尾坐标)
        // ctx.stroke(); //连接首尾
        // ctx.fill();
        rc.path('M-180 0 L-80 100 L20 0', hillOpts);
        rc.path('M-20 0 L80 100 L180 0', hillOpts);
        rc.circle(0, 150, 105, 
            stroke: 'salmon',
            strokeWidth: 4,
            fill: 'gold',
            fillStyle: 'solid',
        );
    </script>
</body>
</html>

实现的效果如下，这里我有个疑问就是为什么y轴左边的这个三角形没有填充到颜色，我试了一下canvas原生的代码是可以填充的，有点搞不懂，知道的大佬还请指导一下，在此先感谢。

如何用向量来描述点和线段？

可以用二维向量来表示这个平面上的点和线段。二维向量其实就是一个包含了两个数值的数组，一个是 x 坐标值，一个是 y 坐标值。

  • 向量和标量一样可以进行数学运算。
  • 一个向量包含有长度和方向信息。

向量运算的意义

向量运算的意义并不仅仅只是用来算点的位置和构造线段，可视化呈现依赖于计算机图形学，而向量运算是整个计算机图形学的数学基础。

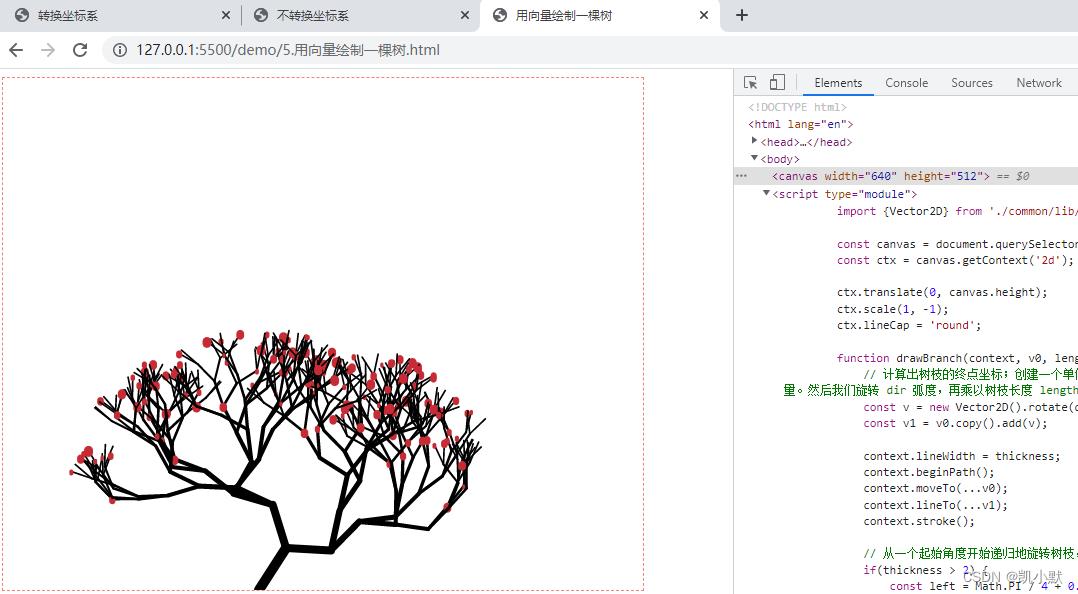
实战演练：用向量绘制一棵树

需要实现的效果如下：

二维旋转矩阵与向量旋转基本思想：处于某二维空间中的任意向量，可以通过标准正交基来表示。通俗来讲，就是用坐标系来表示。不过表示这个向量的不是x轴和y轴坐标，而是二维的基向量。我们可以联想一下物理中的静止参考系和动参考系。动静参考系在这里对应于动静坐标系。向量旋转的同时，动坐标系是相对于这个向量不动的，相对于静止坐标系则旋转同样的角度。只要知道旋转后动坐标系中的标准正交基在静止坐标系中的表达，就能知道旋转后的向量在静止坐标系中的表达。

新建文件 vector2d.js 实现 Vector2D

export class Vector2D extends Array 
    constructor(x = 1, y = 0) 
        super(x, y);
    

    set x(v) 
        this[0] = v;
    

    set y(v) 
        this[1] = v;
    

    get x() 
        return this[0];
    

    get y() 
        return this[1];
    

    get length() 
        return Math.hypot(this.x, this.y);
    

    get dir() 
        return Math.atan2(this.y, this.x);
    

    copy() 
        return new Vector2D(this.x, this.y);
    

    add(v) 
        this.x += v.x;
        this.y += v.y;
        return this;
    

    sub(v) 
        this.x -= v.x;
        this.y -= v.y;
        return this;
    

    scale(a) 
        this.x *= a;
        this.y *= a;
        return this;
    

    cross(v) 
        return this.x * v.y - v.x * this.y;
    

    dot(v) 
        return this.x * v.x + v.y * this.y;
    

    normalize() 
        return this.scale(1 / this.length);
    

    rotate(rad) 
        const c = Math.cos(rad),
            s = Math.sin(rad);
        const [x, y] = this;

        this.x = x * c + y * -s;
        this.y = x * s + y * c;

        return this;

代码实现如下：

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>用向量绘制一棵树</title>
    <style>
        canvas 
            border: 1px dashed salmon;
        
    </style>
</head>
<body>
    <canvas width="640" height="512"></canvas>
    <script type="module">
        import Vector2D from './common/lib/vector2d.js';

        const canvas = document.querySelector('canvas');
        const ctx = canvas.getContext('2d');
        // 以画布左下角为原点
        ctx.translate(0, canvas.height);
        // x 轴向右，y 轴向上的坐标系
        ctx.scale(1, -1);
        ctx.lineCap = 'round';
        /**
         * 画树枝的函数
         * context 是 Canvas2D 上下文
         *   v0 是起始向量
         *   length 是当前树枝的长度
         *   thickness 是当前树枝的粗细
         *   dir 是当前树枝的方向，用与 x 轴的夹角表示，单位是弧度。
         *   bias 是一个随机偏向因子，用来让树枝的朝向有一定的随机性
         * */ 
        function drawBranch(context, v0, length, thickness, dir, bias) 
            // 计算出树枝的终点坐标；创建一个单位向量 (1, 0)，它是一个朝向 x 轴，长度为 1 的向量。然后旋转 dir 弧度，再乘以树枝长度 length。
            const v = new Vector2D().rotate(dir).scale(length);
            const v1 = v0.copy().add(v);

            // 绘制一个固定方向的树枝为根部
            context.lineWidth = thickness;
            context.beginPath();
            context.moveTo(...v0);
            context.lineTo(...v1);
            context.stroke();

            // 从一个起始角度开始递归地旋转树枝，每次将树枝分叉成左右两个分枝        
            if(thickness > 2) 
                const left = Math.PI / 4 + 0.5 * (dir + 0.2) + bias * (Math.random() - 0.5);
                drawBranch(context, v1, length * 0.9, thickness * 0.8, left, bias * 0.9);
                const right = Math.PI / 4 + 0.5 * (dir - 0.2) + bias * (Math.random() - 0.5);
                drawBranch(context, v1, length * 0.9, thickness * 0.8, right, bias * 0.9);
            
            // 随机绘制花瓣
            if(thickness < 5 && Math.random() < 0.3) 
                context.save();
                context.strokeStyle = '#c72c35';
                const th = Math.random() * 6 + 3;
                context.lineWidth = th;
                context.beginPath();
                context.moveTo(...v1);
                context.lineTo(v1.x, v1.y - 2);
                context.stroke();
                context.restore();
            
        
        // 在(256, 0)位置绘制
        const v0 = new Vector2D(256, 0);
        drawBranch(ctx, v0, 50, 10, 1, 3);
    </script>
</body>
</html>

参考资料

以上是关于数学篇05 # 如何用向量和坐标系描述点和线段？的主要内容，如果未能解决你的问题，请参考以下文章

数学篇09 # 如何用仿射变换对几何图形进行坐标变换？

数学篇07 # 如何用向量和参数方程描述曲线？

视觉高级篇22 # 如何用仿射变换来移动和旋转3D物体？

视觉高级篇22 # 如何用仿射变换来移动和旋转3D物体？

如何用OpenGL实现计算机图形学中的平移动画

[线段树系列] LCT打延迟标记的正确姿势