数学篇09 # 如何用仿射变换对几何图形进行坐标变换?
Posted 凯小默
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学篇09 # 如何用仿射变换对几何图形进行坐标变换?相关的知识,希望对你有一定的参考价值。
说明
【跟月影学可视化】学习笔记。
什么是仿射变换?
仿射变换简单来说就是线性变换 + 平移。
仿射变换具有 2 个性质;
- 变换前是直线段的,变换后依然是直线段
- 对两条直线段 a 和 b 应用同样的仿射变换,变换前后线段长度比例保持不变
向量的平移、旋转与缩放
平移
向量 P(x0, y0) 沿着向量 Q(x1, y1) 平移,平移后的向量 p 的坐标。
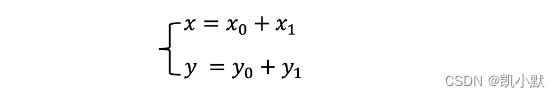
旋转
假设向量 P 的长度为 r,角度是⍺,现在将它逆时针旋转⍬角,此时新的向量 P’ 的参数方程为:

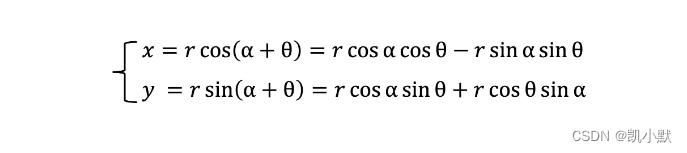
rcos⍺、rsin⍺是向量 P 原始的坐标 (x0,y0),可以写成下面这个公式:

用矩阵表示就是下面的公式:

缩放
向量与标量(标量只有大小、没有方向)相乘即可。

用矩阵表示就是下面的公式:
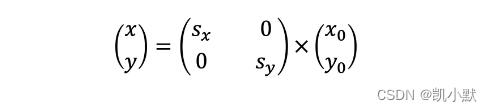
线性变换
上面的旋转和缩放都可以写成矩阵与向量相乘的形式。这种能写成矩阵与向量相乘形式的变换,就叫做线性变换。
- 线性变换不改变坐标原点
- 线性变换可以叠加,多个线性变换的叠加结果就是将线性变换的矩阵依次相乘,再与原始向量相乘。
通用的线性变换公式:比如:向量 P0经过 M1、M2、…Mn 次的线性变换之后得到最终的坐标 P。

仿射变换的一般表达式
向量的基本仿射变换分为平移、旋转与缩放,其中旋转与缩放属于线性变换,而平移不属于线性变换。

仿射变换的公式优化
将上面的仿射变换的一般表达式写成矩阵的形式:用高维度的线性变换表示了低维度的仿射变换。

齐次坐标和齐次矩阵
上面矩阵公式将原本 n 维的坐标转换为了 n+1 维的坐标。这种 n+1 维坐标被称为齐次坐标,对应的矩阵就被称为齐次矩阵。
CSS 的仿射变换
CSS 中的 transform 的作用:对元素进行仿射变换。
transform 不仅支持 translate、rotate、scale 等值,还支持 matrix。CSS 的 matrix 是一个简写的齐次矩阵,因为它省略了 3 阶齐次矩阵第三行的 0, 0, 1 值,所以它 只有 6 个值。
比如:先把 div 旋转 30 度,然后平移 100px、50px,最后再放大 1.5 倍。
div
transform: rotate(30deg) translate(100px,50px) scale(1.5);
其实变换就是

【向量矩阵运算的数学库 math:几乎包含了所有图形学需要用到的数学方法】:https://github.com/oframe/ogl/tree/master/src/math
通过这个库我们转换一下上面的代码,这里使用 multiply 函数

将其改写为矩阵的方式
div
transform: matrix(1.29904, 0.75, -0.75, 1.29904, 61.6025, 93.3013);
matrix 怎么来的,我大致实现了一下:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>CSS 的仿射变换</title>
<style>
.test-box
display: flex;
justify-content: space-around;
.box
width: 100px;
height: 100px;
background-color: salmon;
.box2
transform: rotate(30deg) translate(100px, 50px) scale(1.5);
</style>
</head>
<body>
<h1>kaimo 测试 CSS 的仿射变换</h1>
<div class="test-box">
<div>
<h3>原本的div</h3>
<div class="box box1"></div>
</div>
<div>
<h3> 旋转、平移、放大的div</h3>
<div class="box box2"></div>
</div>
<div>
<h3>矩阵变换后的div</h3>
<div class="box box3"></div>
</div>
</div>
<script type="module">
import multiply from './common/lib/math/functions/Mat3Func.js';
const rad = Math.PI / 6;
const a = [
Math.cos(rad), -Math.sin(rad), 0,
Math.sin(rad), Math.cos(rad), 0,
0, 0, 1
];
const b = [
1, 0, 100,
0, 1, 50,
0, 0, 1
];
const c = [
1.5, 0, 0,
0, 1.5, 0,
0, 0, 1
];
const res = [a, b, c].reduce((a, b) =>
return multiply([], b, a);
);
console.log(res);
// [
// 1.299038105676658, -0.7499999999999999, 61.60254037844388,
// 0.7499999999999999, 1.299038105676658, 93.30127018922192,
// 0, 0, 1
// ]
let mat = [res[0], res[3], res[1], res[4], res[2], res[5]];
document.querySelector(".box3").style.transform = `matrix($[mat])`;
</script>
</body>
</html>
对比效果如下:

仿射变换的应用:实现粒子动画
实现的效果如下:从中心不断的往周围发射三角形,三角形有偏移,旋转,缩放,淡出效果。【点击查看视频效果】

<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>仿射变换的应用:实现粒子动画</title>
<style>
canvas
border: 1px dashed salmon;
</style>
</head>
<body>
<canvas width="512" height="512"></canvas>
<script type="module">
const canvas = document.querySelector("canvas");
const gl = canvas.getContext("webgl");
/**
* glsl 语言编写
* p:当前动画进度,它的值是 u_time / u_duration,取值区间从 0 到 1。
* rad:旋转角度,它的值是初始角度 u_rotation 加上 10π,表示在动画过程中它会绕自身旋转 5 周。
* scale:缩放比例,它的值是初始缩放比例乘以一个系数 p * (2.0 - p)
* 【p * (2.0 - p) 是个缓动函数:能让 scale 的变化量随着时间推移逐渐减小】
* offset:是一个二维向量,它是初始值 u_dir 与 2.0 * p * p 的乘积,u_dir 是个单位向量,2.0 表示它的最大移动距离为 2
* 【p * p 也是一个缓动函数,作用是让位移的变化量随着时间增加而增大。】
* 三个齐次矩阵:
* translateMatrix:是偏移矩阵
* rotateMatrix:是旋转矩阵
* scaleMatrix:是缩放矩阵
* 对顶点进行线性变换:将 pos 的值设置为这三个矩阵与 position 的乘积
* */
const vertex = `
attribute vec2 position;
uniform float u_rotation;
uniform float u_time;
uniform float u_duration;
uniform float u_scale;
uniform vec2 u_dir;
varying float vP;
void main()
float p = min(1.0, u_time / u_duration);
float rad = u_rotation + 3.14 * 10.0 * p;
float scale = u_scale * p * (2.0 - p);
vec2 offset = 2.0 * u_dir * p * p;
mat3 translateMatrix = mat3(
1.0, 0.0, 0.0,
0.0, 1.0, 0.0,
offset.x, offset.y, 1.0
);
mat3 rotateMatrix = mat3(
cos(rad), sin(rad), 0.0,
-sin(rad), cos(rad), 0.0,
0.0, 0.0, 1.0
);
mat3 scaleMatrix = mat3(
scale, 0.0, 0.0,
0.0, scale, 0.0,
0.0, 0.0, 1.0
);
gl_PointSize = 1.0;
vec3 pos = translateMatrix * rotateMatrix * scaleMatrix * vec3(position, 1.0);
gl_Position = vec4(pos, 1.0);
vP = p;
`;
/**
* 在片元着色器中着色实现粒子的淡出效果
* 将动画进度p,从顶点着色器通过变量 varying vP 传给片元着色器
* 然后在片元着色器中让 alpha 值随着 vP 值变化
* */
const fragment = `
precision mediump float;
uniform vec4 u_color;
varying float vP;
void main()
gl_FragColor.xyz = u_color.xyz;
gl_FragColor.a = (1.0 - vP) * u_color.a;
`;
const vertexShader = gl.createShader(gl.VERTEX_SHADER);
gl.shaderSource(vertexShader, vertex);
gl.compileShader(vertexShader);
const fragmentShader = gl.createShader(gl.FRAGMENT_SHADER);
gl.shaderSource(fragmentShader, fragment);
gl.compileShader(fragmentShader);
const program = gl.createProgram();
gl.attachShader(program, vertexShader);
gl.attachShader(program, fragmentShader);
gl.linkProgram(program);
gl.useProgram(program);
// 定义三角形的顶点并将数据送到缓冲区
const position = new Float32Array([
-1, -1,
0, 1,
1, -1,
]);
const bufferId = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, bufferId);
gl.bufferData(gl.ARRAY_BUFFER, position, gl.STATIC_DRAW);
const vPosition = gl.getAttribLocation(program, 'position');
gl.vertexAttribPointer(vPosition, 2, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(vPosition);
// 创建随机三角形属性的函数
function randomTriangles()
const u_color = [Math.random(), Math.random(), Math.random(), 1.0]; // 随机颜色
const u_rotation = Math.random() * Math.PI; // 初始旋转角度
const u_scale = Math.random() * 0.05 + 0.03; // 初始大小
const u_time = 0;
const u_duration = 3.0; // 动画持续时间3秒钟
const rad = Math.random() * Math.PI * 2;
const u_dir = [Math.cos(rad), Math.sin(rad)]; // 运动方向
/**
* performance.now() 方法返回一个精确到毫秒的 DOMHighResTimeStamp
* DOMHighResTimeStamp 是一个 double 类型,用于存储毫秒级的时间值。
* 这种类型可以用来描述离散的时间点或者一段时间(两个离散时间点之间的时间差)。
* */
const startTime = performance.now();
return u_color, u_rotation, u_scale, u_time, u_duration, u_dir, startTime;
/**
* WebGL 的 uniform 的设置:https://developer.mozilla.org/en-US/docs/Web/API/WebGLRenderingContext/uniform
* gl.uniform1f 传入一个浮点数,对应的 uniform 变量的类型为 float
* gl.uniform4f 传入四个浮点数,对应的 uniform 变量类型为 float[4]
* gl.uniform3fv 传入一个三维向量,对应的 uniform 变量类型为 vec3
* gl.uniformMatrix4fv 传入一个 4x4 的矩阵,对应的 uniform 变量类型为 mat4
* */
// 设置 uniform 变量:将随机三角形信息传给 shader
function setUniforms(gl, u_color, u_rotation, u_scale, u_time, u_duration, u_dir)
// gl.getUniformLocation 拿到uniform变量的指针
let loc = gl.getUniformLocation(program, 'u_color');
// 将数据传给 unfirom 变量的地址
gl.uniform4fv(loc, u_color);
loc = gl.getUniformLocation(program, 'u_rotation');
gl.uniform1f(loc, u_rotation);
loc = gl.getUniformLocation(program, 'u_scale');
gl.uniform1f(loc, u_scale);
loc = gl.getUniformLocation(program, 'u_time');
gl.uniform1f(loc, u_time);
loc = gl.getUniformLocation(program, 'u_duration');
gl.uniform1f(loc, u_duration);
loc = gl.getUniformLocation(program, 'u_dir');
gl.uniform2fv(loc, u_dir);
// 使用 requestAnimationFrame 实现动画
let triangles = [];
function update()
for(let i = 0; i < 5 * Math.random(); i++)
triangles.push(randomTriangles());
gl.clear(gl.COLOR_BUFFER_BIT);
// 对每个三角形重新设置u_time
triangles.forEach((triangle) =>
triangle.u_time = (performance.now() - triangle.startTime) / 1000;
setUniforms(gl, triangle);
gl.drawArrays(gl.TRIANGLES, 0, position.length / 2);
);
// 移除已经结束动画的三角形
triangles = triangles.filter((triangle) =>
return triangle.u_time <= triangle.u_duration;
);
requestAnimationFrame(update);
requestAnimationFrame(update);
</script>
</body>
</html>
图形学中必须掌握的数学知识

仿射变换文章推荐
学习资料推荐
以上是关于数学篇09 # 如何用仿射变换对几何图形进行坐标变换?的主要内容,如果未能解决你的问题,请参考以下文章