MATLAB | 如何绘制高斯混合分布分类区域及边界

Posted 2022-09-20 slandarer

在下面这篇中，我们已经说明了如何对数据进行高斯混合分布聚类并绘制概率密度曲面及置信椭圆：https://slandarer.blog.csdn.net/article/details/121521677

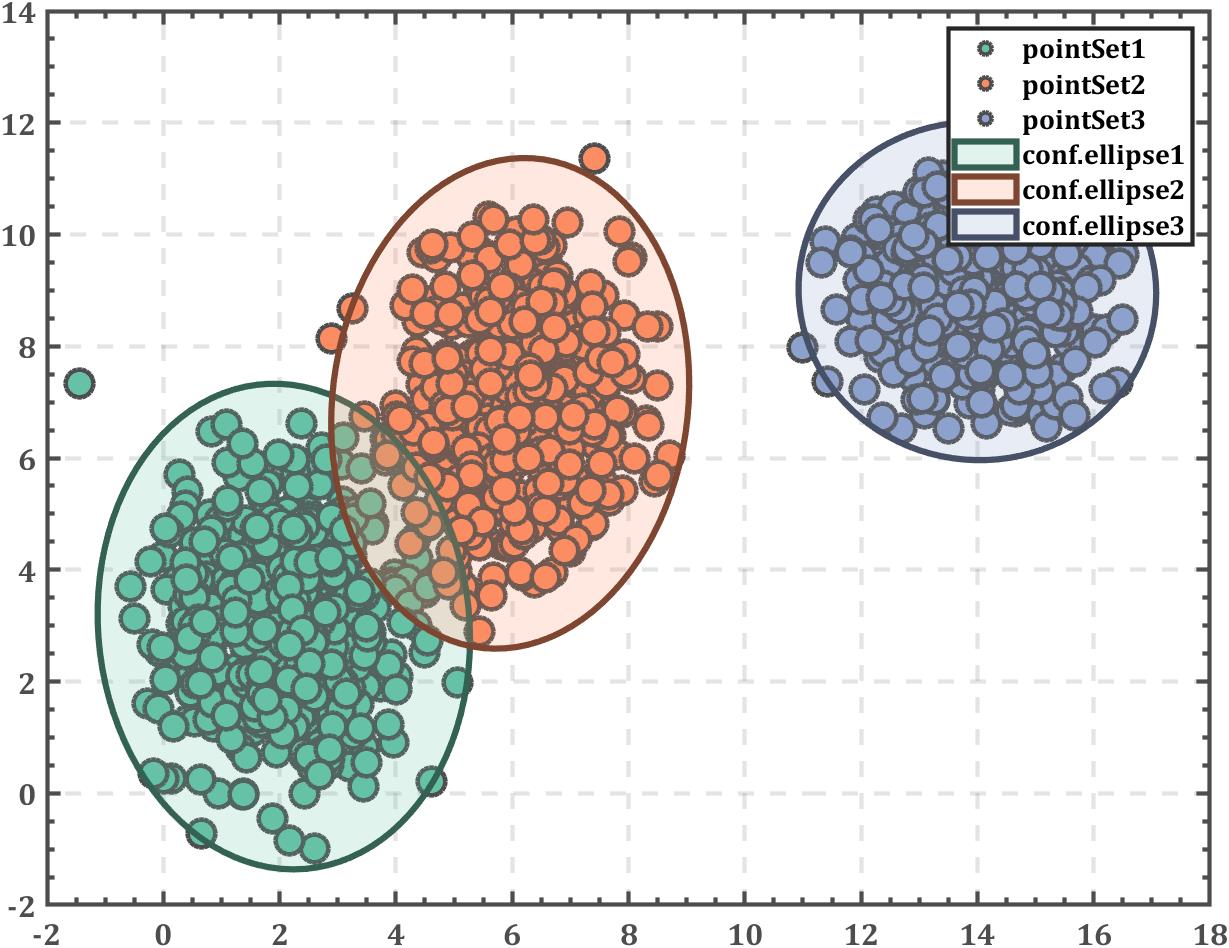
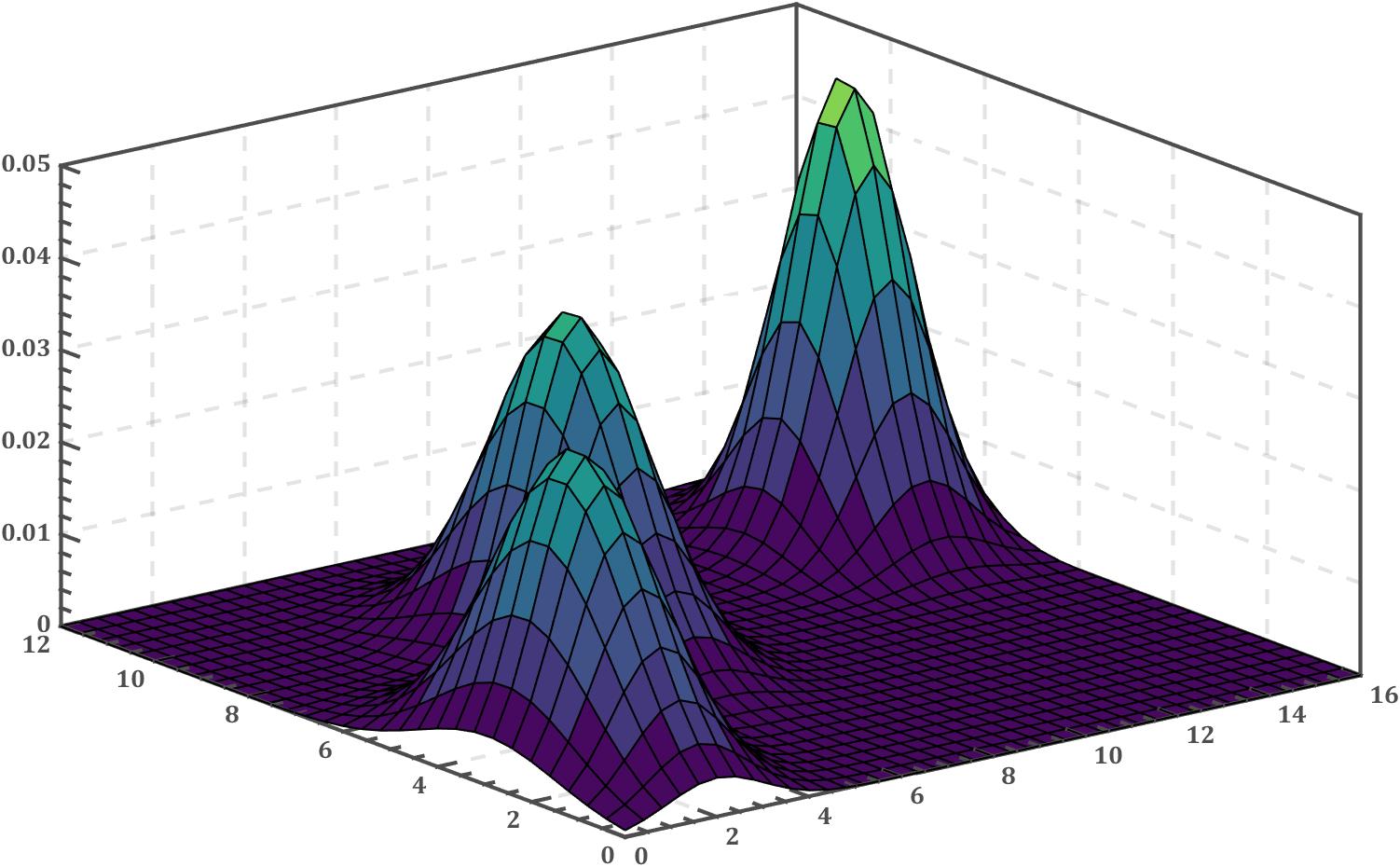
那么这篇要解决的问题就是如何绘制聚类区域与边界：

---

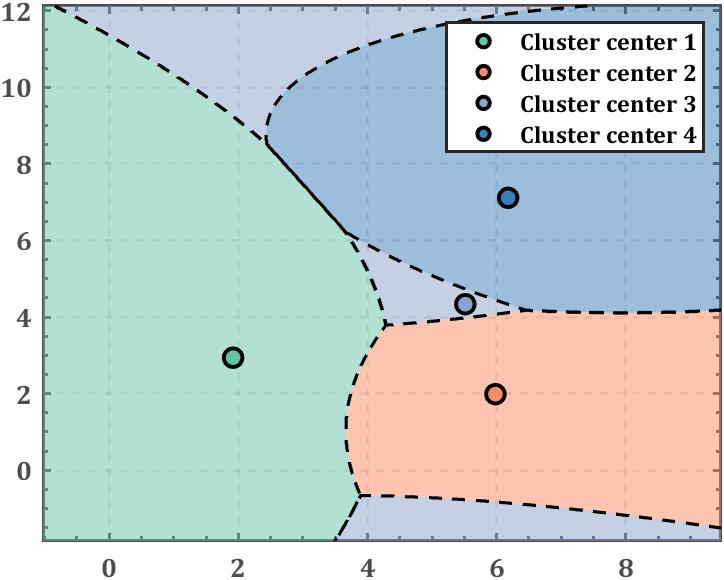
1 工具函数

首先先把工具函数都给出一遍，之后讲解如何绘制绘制聚类区域与边界：

1.1 高斯混合模型聚类

function [Mu,Sigma,Pi,Class]=gaussKMeans(pntSet,K,initM)
% @author:slandarer
% ===============================================================
% pntSet  | NxD数组   | 点坐标集                                |
% K       | 数值      | 划分堆数量                              |
% --------+-----------+-----------------------------------------+
% Mu      | KxD数组   | 每一行为一类的坐标中心                  |
% Sigma   | DxDxK数组 | 每一层为一类的协方差矩阵                |
% Pi      | Kx1列向量 | 每一个数值为一类的权重(占比)            |
% Class   | Nx1列向量 | 每一个数值为每一个元素的标签(属于哪一类)|
% --------+-----------+-----------------------------------------+


[N,D]=size(pntSet); % N:元素个数 | D:维数

% 初始化数据===============================================================
if nargin<3
    initM='random';
end
switch initM
    case 'random' % 随机取初始值
        [~,tIndex]=sort(rand(N,1));tIndex=tIndex(1:K);
        Mu=pntSet(tIndex,:);

    case 'dis'    % 依据各维度的最大最小值构建方向向量
                  % 并依据该方向向量均匀取点作为初始中心       
        tMin=min(pntSet);
        tMax=max(pntSet);
        Mu=linspace(0,1,K)'*(tMax-tMin)+repmat(tMin,K,1);

    % case '依据个人需求自行添加'  
    % ... ...
    % ... ...     
end

% 一开始设置每一类有相同协方差矩阵和权重
Sigma(:,:,1:K)=repmat(cov(pntSet),[1,1,K]);
Pi(1:K,1)=(1/K);

% latest coefficient:上一轮的参数
LMu=Mu;        
LPi=Pi;
LSigma=Sigma;

turn=0; %轮次

% GMM/gauss_k_means主要部分================================================
while true
    
    % 计算所有点作为第k类成员时概率及概率和(不加权重)
    % 此处用了多次转置避免构建NxN大小中间变量矩阵
    % 而将过程中构建的最大矩阵缩小至NxD，显著减少内存消耗
    Psi=zeros(N,K);
    for k=1:K
        Y=pntSet-repmat(Mu(k,:),N,1);
        Psi(:,k)=((2*pi)^(-D/2))*(det(Sigma(:,:,k))^(-1/2))*...
                      exp(-1/2*sum((Y/Sigma(:,:,k)).*Y,2))';    
    end
    
    % 加入权重计算各点属于各类后验概率
    Gamma=Psi.*Pi'./sum(Psi.*Pi',2);
    
    % 大量使用矩阵运算代替循环，提高运行效率
    Mu=Gamma'*pntSet./sum(Gamma,1)';
    for k=1:K
        Y=pntSet-repmat(Mu(k,:),N,1);
        Sigma(:,:,k)=(Y'*(Gamma(:,k).*Y))./sum(Gamma(:,k));
    end
    Pi=(sum(Gamma)/N)';
    [~,Class]=max(Gamma,[],2);

    % 计算均方根误差
    R_Mu=sum((LMu-Mu).^2,'all');
    R_Sigma=sum((LSigma-Sigma).^2,'all');
    R_Pi=sum((LPi-Pi).^2,'all');
    R=sqrt((R_Mu+R_Sigma+R_Pi)/(K*D+D*D*K+K));
    
    % 每隔10轮输出当前收敛情况
    turn=turn+1;
    if mod(turn,10)==0
        disp(' ')
        disp('==================================')
        disp(['第',num2str(turn),'次EM算法参数估计完成'])
        disp('----------------------------------')
        disp(['均方根误差:',num2str(R)])
        disp('当前各类中心点：')
        disp(Mu)
    end
    
    % 循环跳出
    if (R<1e-6)||isnan(R)
        disp(['第',num2str(turn),'次EM算法参数估计完成'])
        if turn>=1e4||isnan(R)
            disp('GMM模型不收敛')
        else
            disp(['GMM模型收敛，参数均方根误差为',num2str(R)])
        end
        break;
    end   
    LMu=Mu;
    LSigma=Sigma;
    LPi=Pi;
end
end

1.2 概率密度函数获取

就是一个比较复杂的函数获取(公式显示不全可左右滑动)：

首先是高斯分布的函数：

$$\mathcal{N}(\mathbf{x}\mid \mathbf{\mu },\mathbf{\Sigma })=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\mathbf{\Sigma }{|}^{1/2}}\exp \left[-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })\right]$$

那么高斯混合分布的函数就是好几个上面的高斯分布函数乘以系数再相加：
$$p(\mathbf{x})=\sum _{k=1}^K{\pi }_k\mathcal{N}\left(\mathbf{x}\mid {\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k\right)$$

function func=getGaussFunc(Mu,Sigma,Pi)
[K,D]=size(Mu);

XD=[];
for d=1:D
    Xd=['x',num2str(d)];
end
X=sym(X);

func=0;
for k=1:K
    tMu=Mu(k,:);
    tSigma=Sigma(:,:,k);   
    tPi=Pi(k);
    tX=X-tMu;   
    func=func+tPi*(1/(2*pi)^(D/2))*(1/det(tSigma)^(1/2))*exp((-1/2)*(tX/tSigma*tX.'));
end

func=matlabFunction(func);
end

1.3 置信椭圆获取

function [X,Y]=getEllipse(Mu,Sigma,S,pntNum)
% 置信区间 | 95%:5.991  99%:9.21  90%:4.605
% (X-Mu)*inv(Sigma)*(X-Mu)=S

invSig=inv(Sigma);

[V,D]=eig(invSig);
aa=sqrt(S/D(1));
bb=sqrt(S/D(4));

t=linspace(0,2*pi,pntNum);
XY=V*[aa*cos(t);bb*sin(t)];
X=(XY(1,:)+Mu(1))';
Y=(XY(2,:)+Mu(2))';
end

---

2 聚类区域及边界绘制

2.1 数据及混合模型

以下是随机生成的一组数据，对其进行一次高斯混合分布聚类：

% 构造三个符合高斯分布的点集并合并
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([6 7],[1 0;0 2],500);
PntSet3=mvnrnd([6 2],[1 0;0 1],500);
MATLAB实现高斯混合分布的EM算法及二维时概率密度曲面置信椭圆绘制

 MATLAB实现高斯混合分布的EM算法及二维时概率密度曲面置信椭圆绘制
 如何在 MATLAB 中绘制显示二维高斯函数总和的图像？
 使用 matlab 进行一维高斯贝叶斯分类
 matlab如何产生服从高斯分布的随机整数
 Matlab中的无环高斯混合模型