算法小讲堂之B树和B+树(浅谈)|考研笔记
Posted MangataTS
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法小讲堂之B树和B+树(浅谈)|考研笔记相关的知识,希望对你有一定的参考价值。
文章目录
一、前言
前面学习了平衡二叉树( A V L AVL AVL 树),我们知道了平衡的概念就是让树尽量的 “胖” ,让它的高度不会线性增长,那么这篇笔记主要是分享 B B B 树和 B + B+ B+ 树的原理、应用(不涉及代码实现,也许有一天会补上,谁知道呢)
二、定义
B B B 树(又称 B − B- B− 树)和 B + B+ B+ 树其实差别不是很大,所以我会着重介绍 B B B 树,然后最后指出 B + B+ B+ 树的不同点
那么什么是 B B B 树呢?
B B B 树,又称 多路平衡查找树 , B B B 树中所有结点的孩子个数的最大值称为 B B B 树的 阶 ,通常用 m m m 表示。
这里的多路其实就是指这一颗树可能不只是最多有两颗子树,具体多少颗是由 B B B 树的阶决定的,作为一颗 B B B 树应该满足一下要求:
- ①若根节点不是 叶结点 ,则至少有两个子树(即一个关键字)
- ②除了根结点外,其他每个结点至少有 m 2 \\fracm2 2m 个子树,最多有 m m m 个子树,对应的每一个结点至少有 ⌈ m 2 − 1 ⌉ \\left \\lceil \\fracm2 -1 \\right \\rceil ⌈2m−1⌉ 个关键字
- ③每一个结点的关键字从左到右升序排列
- ④ B B B 树是一个严格的多路平衡查找树,它的左右子树的高度室相等的,且叶结点处于同一层(即所有结点的平衡因子都为 0 0 0 )
上面提到的关键字就是对于每一个结点可能会存在多个值的情况,这些值按照升(降)序排列,用于划分子树区间,之前的二叉平衡树我们对于每一个结点只有一个关键字,我们就有两个分支,显然若是有 m m m 个关键字则会有 m + 1 m+1 m+1 个分支,其实这就是一个简单的区间划分(相邻关键字划分一个区间、前后俩结点单独一个分区)
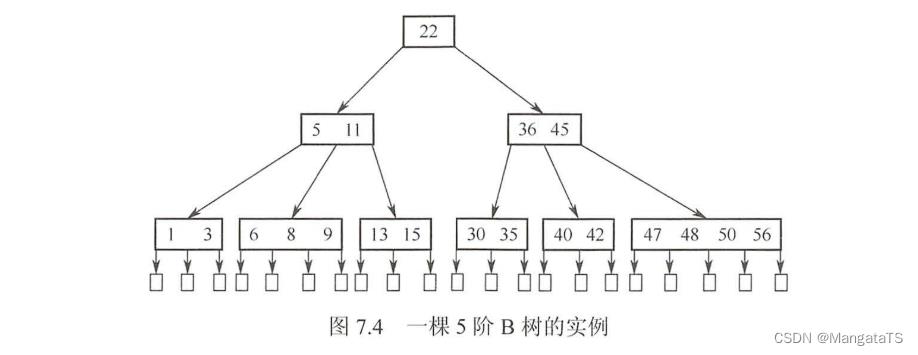
PS:这里需要注意一下,在王道的书上是将叶结点(P285页)定义成了不存在的一层,但是在严蔚敏的书上定义的就是最后一层有关键字的结点,比如下图中,王道将第四层定义为叶子节点,严蔚敏的书上认为叶子结点(终端节点)是第三层,而笔者也认为第三层才是叶子节点或者称为终端节点
三、原理
3.1 树的高度
假设一颗二叉树包含 n ( n > = 1 ) n(n>=1) n(n>=1) 个关键字、高度为 h h h ,阶数为 m m m 的 B B B 树
- 至少高度:
既然是至少高度,那么我们应该尽量希望每个结点的关键字都是满即 m − 1 m-1 m−1 的,于是我们得到了如下不等式:
∵ n < = ( m − 1 ) ( 1 + m + m 2 + … … + m h − 1 ) n < = m h − 1 ∴ h > = l o g m ( n + 1 ) ∵ n <=(m-1)(1+m+m^2+……+m^h-1) \\\\ n <= m^h - 1 \\\\ ∴ h>=log_m(n+1) ∵n<=(m−1)(1+m+m2+……+mh−1)n<=mh−1∴h>=logm(n+1)
- 至多高度:
既然是至多,那么我们尽可能希望每一个结点的关键字都是最少的即 ⌈ m 2 ⌉ \\left \\lceil \\fracm2 \\right \\rceil ⌈2m⌉ ,前面也提到了根节点可以特殊一下 最少一个关键字
那么我们会发现,第一层至少有 1 1 1 个结点,第二层至少有 2 2 2 个结点,第三层至少有 2 ⌈ m 2 ⌉ 2\\left \\lceil \\fracm2 \\right \\rceil 2⌈2m⌉ 个结点……第 h + 1 h+1 h+1 层至少有 2 ⌈ m 2 ⌉ h − 2 2\\left \\lceil \\fracm2 \\right \\rceil ^h-2 2⌈2m⌉h−2 这一层就是不包含关键字的一层,即查找失败的一层,又因为关键字的个数为 n n n 那么说明第 h + 1 h+1 h+1 层最少 n + 1 n+1 n+1 个结点,于是我们得到:
∵ n + 1 > = 2 ( ⌈ m 2 ⌉ ) h − 1 ∴ h < = l o g ⌈ m 2 ⌉ n + 1 2 + 1 ∵n+1>=2(\\left \\lceil \\fracm2 \\right \\rceil)^h-1 \\\\ \\\\ ∴ h <= log_\\left \\lceil \\fracm2 \\right \\rceil\\fracn+12 + 1 ∵n+1>=2(⌈2m⌉)h−1∴h<=log⌈2m⌉2n+1+1
假设一颗 3 3 3 阶 B B B 树一共有 8 8 8 个关键字,那么其树的高度范围为: 2 < = h < = 3.17 2<=h<=3.17 2<=h<=3.17
3.2 查找操作
前面也说了 B B B 树的每一个结点在内部都是有序排列的,并且结点与结点之间也是有一定关系的,在之前的平衡二叉树中,我们有两条路的分支,但是在 B B B 树的查找中我们需要根据结点的多路分支做决定,那么其实查找操作和前面的平衡二叉树|二叉查找树是一样的啦
- ①先让查找值和 B B B 树的根节点的第一个关键字比较,若是匹配,则查找成功
- ②若是匹配不成功继续和后面的关键字匹配,若是找到匹配,则匹配成功
- ③若是找到一个大于查找值的关键字,那么就需要往这个关键字和前一个关键字之间的分支结点往下搜索,继续重复上面的关键字匹配操作
- ④若是当前结点最后一个关键字比当前查找的值还小,那么就继续往该结点的最右分支往下继续搜索,重复上面的操作
- ⑤若是结点查找到了空结点,那么说明查找失败
3.3 插入操作
先通过上面的定位操作定位到一个查找失败的结点,然后检查该节点的父结点的关键字个数,若是关键字个数小于 m − 1 m-1 m−1 那么说明可以直接插入到该节点(叶子节点),否则的话插入后会引起结点的分裂,因为要维护平衡的关系
分裂的方法:
- 取一个新结点,在插入 k e y key key 后的原结点, 从中间位置 ⌈ m 2 ⌉ \\left \\lceil \\fracm2 \\right \\rceil ⌈2m⌉将其中的关键宇分为两部分
- 左部分包含的关键宇放在原结点中, 右部分包含的关键宇放到新结点中,中间位置 ⌈ m 2 ⌉ \\left \\lceil \\fracm2 \\right \\rceil ⌈2m⌉ 的结点插入原结点的父结点 。
- 若此时导致其父结点的关键字个数也超过了上限,则继续进行这种分裂操作, 直至这个过程传到根结点为止 ,进而导致 B B B 树高度增 1 1 1
例如下面的分裂操作:
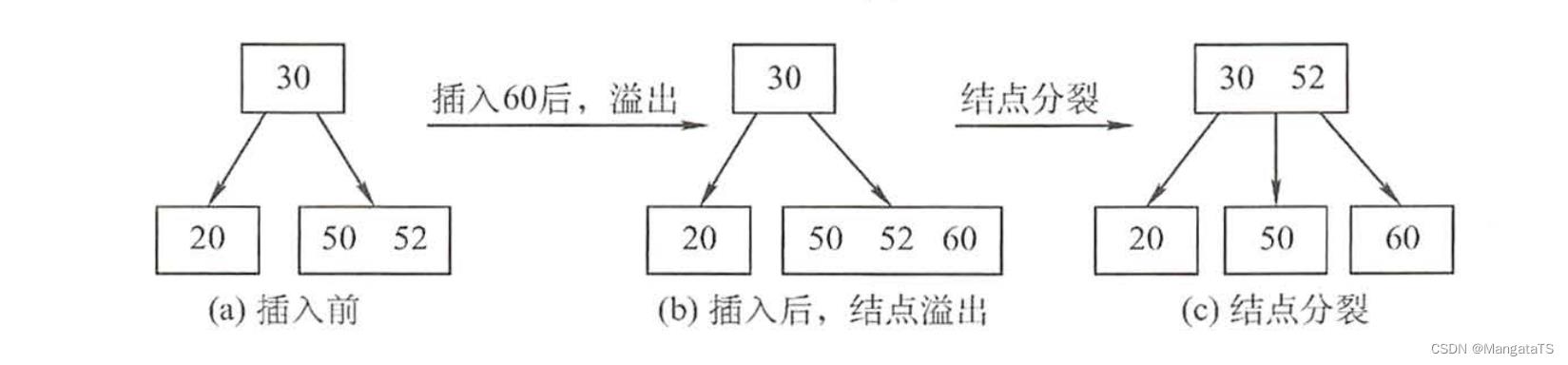
我们可以来观察这个过程:
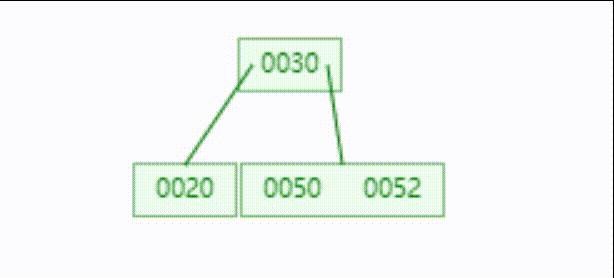
实际上就是将 ⌈ m 2 ⌉ \\left \\lceil \\fracm2 \\right \\rceil ⌈2m⌉ 位置的关键字直接变为其左边和右边关键字的父节点,然后因为要往上贡献一个关键字,这可能会导致父节点层分裂,然后继续向上贡献一个关键字,以此类推,直到停止贡献,或者到达根节点,分裂出新的根,比如在上面的插入 52 52 52 后我们再插入 61 、 62 61、62 61、62 就会让这棵树的高度拔高一层,流程如下:
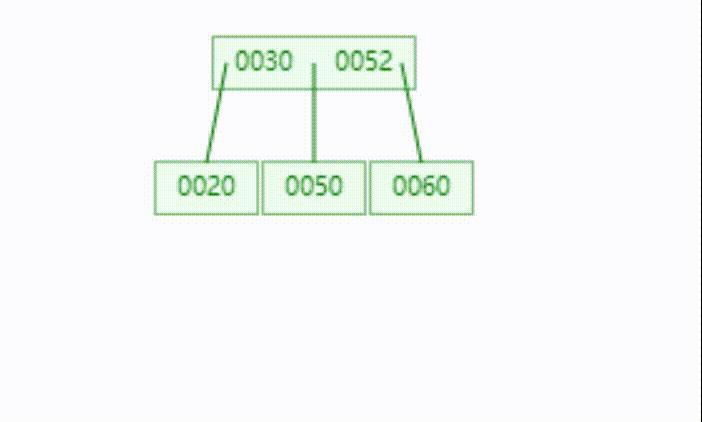
3.4 删除操作
删除操作要更加复杂一点,大体分为两种情况:
3.4.1 删除关键字是非叶子结点
那么我们直接将该结点的前驱(后驱)关键字拿来顶替就行,例如下图删除
80
80
80 的情况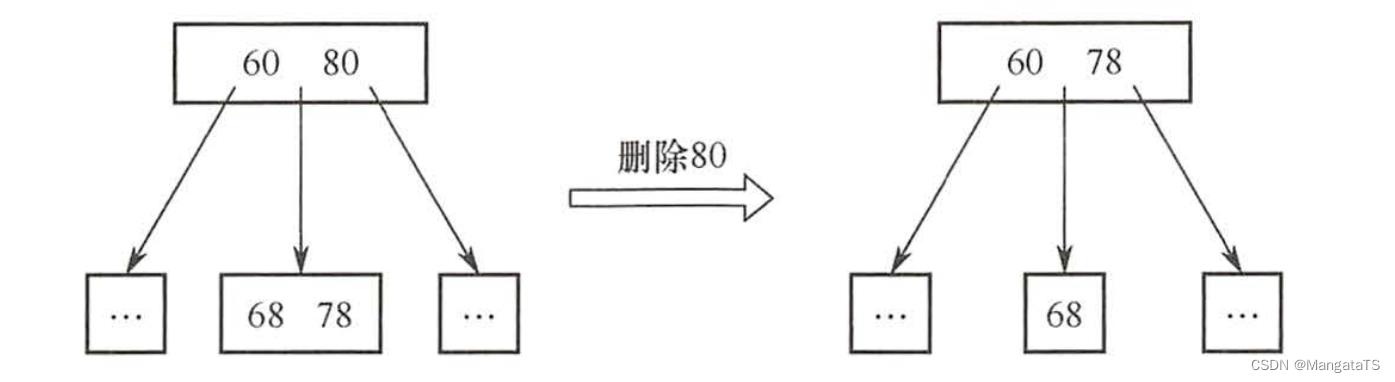
3.4.2 删除关键字是叶子结点
主要分为三种情况:
- 一、如果删除关键字后该结点的关键字个数仍然大于等于 ⌈ m 2 ⌉ \\left \\lceil \\fracm2 \\right \\rceil ⌈2m⌉ 那么直接删除就完事
- 二、如果删除关键字后该结点的关键字个数等于
⌈
m
2
−
1
⌉
\\left \\lceil \\fracm2-1 \\right \\rceil
⌈2m−1⌉
- ①如果兄弟结点够借,即与此结点同一层的临近的右(左)兄弟结点的关键字个数大于等于
⌈
m
2
⌉
\\left \\lceil \\fracm2 \\right \\rceil
⌈2m⌉ 那么就可以将父结点的关键字填充到当前结点,然后再将兄弟结点的关键字移到父结点上
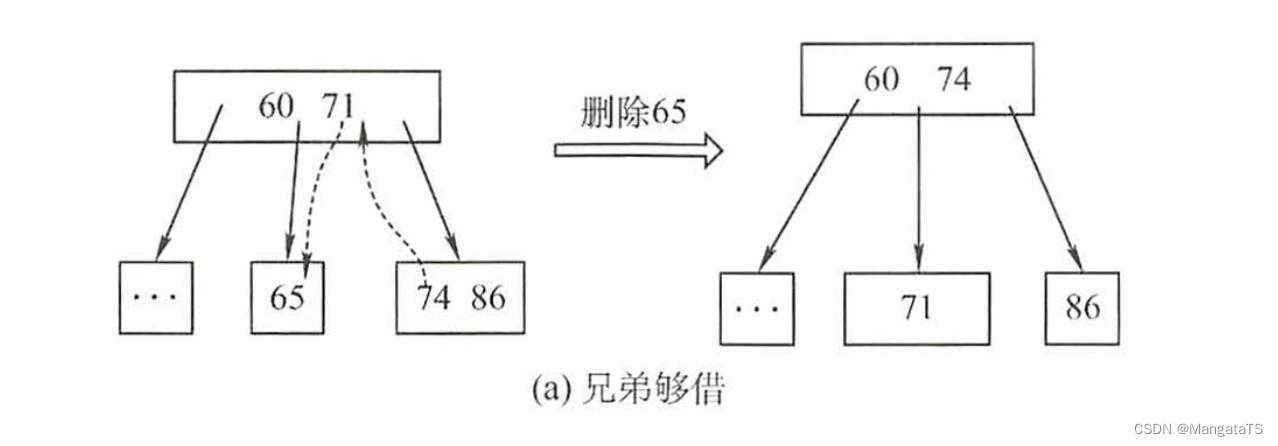
- ②如果兄弟结点不够借,即与此结点同一层的临近的右(左)兄弟结点的关键字个数等于 ⌈ m 2 − 1 ⌉ \\left \\lceil \\fracm2 -1\\right \\rceil ⌈2第七节1:Java集合框架之二叉排序树和哈希表
- ①如果兄弟结点够借,即与此结点同一层的临近的右(左)兄弟结点的关键字个数大于等于
⌈
m
2
⌉
\\left \\lceil \\fracm2 \\right \\rceil
⌈2m⌉ 那么就可以将父结点的关键字填充到当前结点,然后再将兄弟结点的关键字移到父结点上