算法小讲堂之你真的会双指针吗？

Posted 2022-03-09 MangataTS

长文预告！！！

双指针算法

双指针又被称为 尺取法 双指针是一种简单而又灵活的技巧和思想，并不是一种具体的算法，单独使用可以轻松解决一些特定问题，和其他算法结合也能发挥多样的用处。

双指针顾名思义，同时使用两个指针维护或者是统计一些区间信息的。特别是在数组、链表等数据结构中，双指针的算法能大大减少我们的编码速度以及时间复杂度，双指针大体的应用分为以下三个大类： 滑动窗口 、 碰撞指针 、 快慢指针

一、滑动窗口

1.1 维护区间和|积

1.1.1 问题引出

选自Subsequence (POJ No.3061)

给定长度为 $N(10<N<10^5)$ 的正整数数列 $a_0,a_1,\dots \dots ,a_{n-1}$ 以及正整数 $S(0<S<10^8)$ 。求出总合不小于S的 连续 子序列长度的最小值。如果解不存在，则输出0

样例：

10 15
5 1 3 5 10 7 4 9 2 8

2

1.1.2 朴素想法

我们枚举子序列的左端点，然后再枚举长度，以及再一个循环来计算 $[l,r]$ 这个区间的一个权值和，然后从满足条件的序列里面挑选出最短的一个，那么复杂度就为 $O(N^3)$ , 代码如下：

#include<iostream>
#include<algorithm>
using namespace std;

#define ll long long

const int N = 1e5+10;
ll a[N],S,n;

int main()

	int t;
	cin>>t;
	while(t--)
		cin>>n>>S;
		int ans = 0x3f3f3f3f;
		for(int i = 1;i <= n; ++i) cin>>a[i];
		for(int l = 1;l <= n; ++l)
			for(int len = 1;l + len - 1 <= n; ++len) 
				int r = l + len - 1;
				ll sum = 0;
				for(int j = l;j <= r; ++j)
					sum += a[j];
				if(sum >= S) 
					ans = min(ans,len);
			
		
		if(ans == 0x3f3f3f3f) cout<<0<<endl;
		else cout<<ans<<endl;
	
	
	return 0;

1.1.3 前缀和优化

当然 $O(N^3)$ 的复杂度远远不够，于是我们发现在最内层的计算区间和的循环可以用前缀和优化掉，那么优化后代码如下：

#include<iostream>
#include<algorithm>
using namespace std;

#define ll long long

const int N = 1e5+10;
ll a[N],S,n,pre[N];

int main()

	int t;
	cin>>t;
	while(t--)
		cin>>n>>S;
		int ans = 0x3f3f3f3f;
		for(int i = 1;i <= n; ++i) cin>>a[i],pre[i]=pre[i-1] + a[i];
		for(int l = 1;l <= n; ++l)
			for(int len = 1;l + len - 1 <= n; ++len) 
				int r = l + len - 1;
				ll sum = pre[r]-pre[l-1];
				if(sum >= S) 
					ans = min(ans,len);
			
		
		if(ans == 0x3f3f3f3f) cout<<0<<endl;
		else cout<<ans<<endl;
	
	
	return 0;

1.1.4 二分优化

现在我们以及将复杂度降到了 $O(N^2)$ 了，但是对于这个问题而言，显然是不够看的，于是我们得再想一下优化，不难发现由于数组中的元素都是正整数，那么说明我们的前缀和是一个单调递增的序列，那么我们就能通过二分法来加速我们寻找可行长度，而不是从1开始枚举，于是我们得到了这样的代码：

#include<iostream>
#include<algorithm>
using namespace std;

#define ll long long

const int N = 1e5+10;
ll a[N],S,n,pre[N];

int main()

	int t;
	cin>>t;
	while(t--)
		cin>>n>>S;
		int ans = 0x3f3f3f3f;
		for(int i = 1;i <= n; ++i) cin>>a[i],pre[i] = pre[i-1] + a[i];
		for(int l = 1;l <= n; ++l)
			int r = lower_bound(pre+1,pre+n+1,S+pre[l-1]) - pre;
			if(r > n) continue;
			ans = min(ans,r-l+1);
		
		if(ans == 0x3f3f3f3f) cout<<0<<endl;
		else cout<<ans<<endl;
	
	
	return 0;

此时我们的时间复杂度为 $O(Nlo{g}_N)$ ，对于这一道题来说算是绰绰有余了，但是这不是最优解或者说不算一个比较理想的解法

1.1.5 双指针做法

于是引出了我们今天的主角 ： “双指针算法”

• 1.我们定义两个指针： $l$ 和 $r$ 在初始时刻都指向第一个元素，并且将子区间的和置为 $a[1]$

• 2.然后我们挪动 $r$ 指针一直到大于等于 $S$ 位置，然后我们 统计当前的长度 ，后面的完全不用去遍历了，因为前缀和是单调递增的所以当前位置就是最优的

• 3.然后我们将左指针 $l$ 往右移动一位，

• 4.然后再看 $r$ 指针是否能移动，也就是重复上面的 $r$ 指针移动的过程，最后如果我们发现 $r$ 指针以及移动到末尾了，并且当前的和还是小于 $S$ 的，那么说明后面也不可能再有这种区间满足条件了，所以可以直接 break

最后我们的ans如果没更新的话说明就没有满足的区间，当然这个也可以通过求和判断是否会存在

上面样例的一个图解：

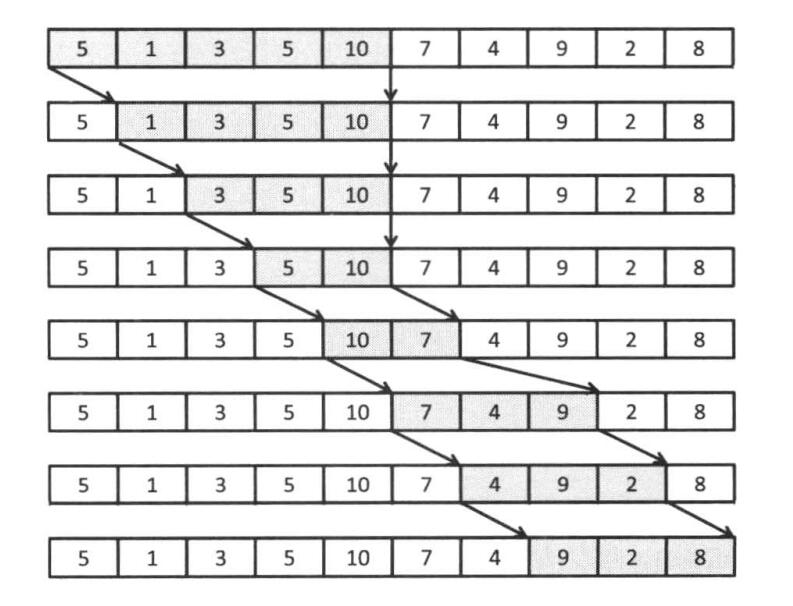
那么我们不难得出如下代码：

#include<iostream>
#include<algorithm>
using namespace std;

#define ll long long

const int N = 1e5+10;
ll a[N],S,n,pre[N];

int main()

	int t;
	cin>>t;
	while(t--)
		cin>>n>>S;
		int ans = 0x3f3f3f3f;
		for(int i = 1;i <= n; ++i) cin>>a[i];
		int l = 1,r = 1;
		ll sum = a[1];
		while(r <= n) 
			while(r <= n && sum < S) sum += a[++r];
			if(sum < S) break;
			ans = min(ans,r-l+1);
			sum -= a[l++];
		
		if(ans == 0x3f3f3f3f) cout<<0<<endl;
		else cout<<ans<<endl;
	
	
	return 0;

我们来分析这个代码的复杂度，对于 $l$ 和 $r$ 指针我们没有进行回溯操作，也就是说对于两个指针而言最多覆盖整个数组长度，也就是 $O(N)$ 的，并且在思路上双指针的做法也会比前缀和+二分优化好，空间利用率也比较高，但是有的时候可能双指针会搭配二分一起用，这些东西就需要读者刷题踩坑啦，我就不多赘述了。

1.2 最小可行区间

1.2.1 问题引出

选自 Jessica’s Reading Problem (POJ No.3320)

为了准备考试，$Jessica$ 开始读一本很厚的课本。要想通过考试，必须把课本中所有的知识点都掌握。这本书总共有P页，第 $i$ 页恰好有一个知识点 $a_i$ (每个知识点都有一个整数编号 ）。全书中同一个知识点可能会被多次提到，所以她希望通过阅读其中连续的一些页把所有的知识点都覆盖到。给定每页写到的知识点，请求出要阅读的最少页数。

样例：
输入：

5
1 8 8 8 1

输出：

2

1.2.2 思路

首先我们要统计有多少本书（数量为 $len$ ），这个我们可以用 set 或者 map 容器来统计，然后同样的

• 1.我们定义 $l$ 和 $r$ 两个指针,两者都初始化为首位置 $1$ 统计访问次数的可以使用 map<int,int> 容器来存储信息
• 2.然后我们将 $r$ 指针不断往后移动直到满足不同书本数 $res$ 和 $len$ 相等，在将 $r$ 指针不断后移的过程中，我们只计算当前访问次数值为0的书本数即可（即出现新书的时候我们的数的种类res才会更新）
• 3.如果我们发现循环结束后我们的 $res$ 即书本数量比 $n$ 小的话说明后面也不再可能会有满足条件的子序列了
• 4.然后我们统计当前的长度，并更新 $ans$ 的结果，同时将 $l$ 指针右移一步

于是我们就能得到如下代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<set>
#include<map>
using namespace std;

#define ll long long

const int N = 1e5+10;
int a[N],n;

int main()

	scanf("%d",&n);
	set<int> S;
	for(int i = 1;i <= n; ++i) scanf("%d",&a[i]),S.insert(a[i]);
	int len = S.size();
	map<int,int> vis;
	vis.clear();
	int l = 1,r = 1,res = 0;
	int ans = 0x3f3f3f3f;
	while(l <= r)
		while(r <= n && res < len)
			if(vis[a[r]] == 0) res++;
			vis[a[r++]]++;
		
		if(res < len) break;
		ans = min(ans,r-l);
		if(--vis[a[l++]] == 0) res--;
	
	printf("%d\\n",ans);
	return 0;

注意这里的写法和上面的有点不太一样，就在于第一个位置我们在这里并没有直接算上，是因为不算上的话在后面的处理中不用考虑边界情况，这一点读者们可以自己下来手动模拟一下

1.3 固定窗口滑动

1.3.1 问题引出

给定长度为 $n(k<=n<=10^6)$ 的数列 a 0 a 1 a 2 …

以上是关于算法小讲堂之你真的会双指针吗？的主要内容，如果未能解决你的问题，请参考以下文章

有点意思之你真的了解对象的键值

算法小讲堂之B树和B+树（浅谈）|考研笔记

宿舍小讲堂 || 动态规划算法及其应用

算法小讲堂之拓扑排序

算法小讲堂之最短路算法(Floyd+bellman+SPFA+Dijkstra)

算法小讲堂之关键路径