LeetCode 0478.在圆内随机生成点

Posted 2022-06-07 Tisfy

【LetMeFly】通俗的话描述 478.在圆内随机生成点 の 两种方法

力扣题目链接：https://leetcode.cn/problems/generate-random-point-in-a-circle/

给定圆的半径和圆心的位置，实现函数 randPoint ，在圆中产生均匀随机点。

实现 Solution 类:

• Solution(double radius, double x_center, double y_center) 用圆的半径 radius 和圆心的位置 (x_center, y_center) 初始化对象
• randPoint() 返回圆内的一个随机点。圆周上的一点被认为在圆内。答案作为数组返回 [x, y] 。

 

示例 1：

输入: 
["Solution","randPoint","randPoint","randPoint"]
[[1.0, 0.0, 0.0], [], [], []]
输出: [null, [-0.02493, -0.38077], [0.82314, 0.38945], [0.36572, 0.17248]]
解释:
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint ();//返回[-0.02493，-0.38077]
solution.randPoint ();//返回[0.82314,0.38945]
solution.randPoint ();//返回[0.36572,0.17248]

 

提示：

• 0 < radius <= 108
• -107 <= x_center, y_center <= 107
• randPoint 最多被调用 3 * 104 次

题目大意

给你一个⚪的圆心和半径，让你每次随机从⚪内取一点并返回其坐标。

自定义Rand函数

因为此题可能会经常用到double范围内的随机数，因此可以自定义两个rand函数来方便调用

/* 返回double类型的[l, r]范围内的随机数 */
double rand(double l, double r) 
    return (double)1 * rand() * (r - l) / RAND_MAX + l;

/* 返回double类型的[0, r]范围内的随机数 */
double rand(double r) 
    return rand(0, r);

很Rand的Rand

我们还可以用std::mt19937来产生高性能的随机数。

// 初始化
mt19937 genrandom_device();
uniform_real_distribution<double> dis(l, r);

// 使用
double x = dis(gen);

方法一：矩形rand圆里接受（拒绝采样）

圆形里面不是不好直接rand吗？因此我们可以先在圆的邻接矩阵中随机rand，看是否落到了圆里。

引用一张 @LeetCode-Solution的图片：

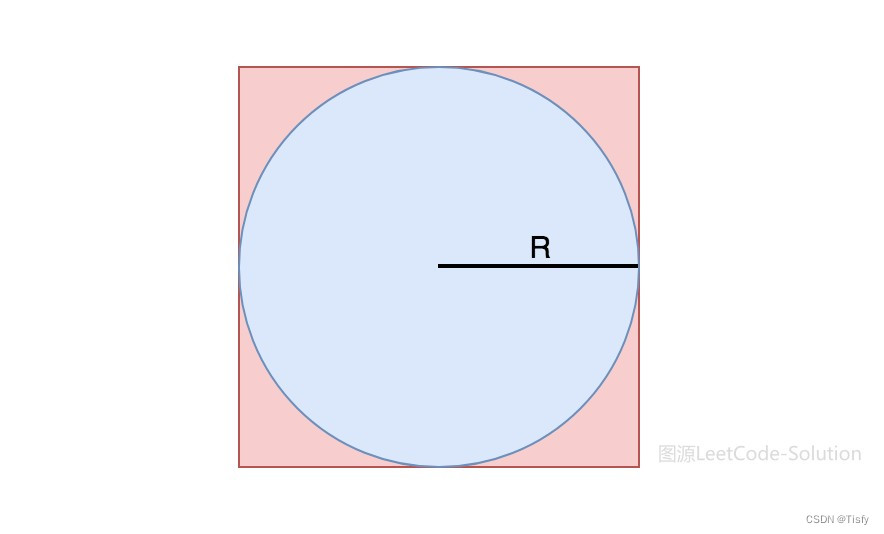
我们随机rand x和y，这样rand出来的点就会落在矩形里。如果点落在了蓝色范围内，就返回这个点作为结果。否则落在红色区域内的话就继续rand。

这个方法似乎有一个比较官方的名字，叫“拒绝采样”。（大概意思就是如果采用结果不在合法范围内就拒绝这个样本）

• 时间复杂度$O(1)$，期望值是$O(1)$，因为期望每$\frac{4r^2}{\pi r^2}\approx \frac{1}{0.785}\approx 1.274$ 次采样
• 空间复杂度$O(1)$

AC代码

C++

const double PI = acos(-1);

inline double rand(double l, double r) 
    return (double)1 * rand() * (r - l) / RAND_MAX + l;


inline double rand(double r) 
    return rand(0, r);


class Solution 
private:
    double radius;
    double x_center;
    double y_center;
public:
    Solution(double radius, double x_center, double y_center) 
        srand(time(NULL));
        this->radius = radius;
        this->x_center = x_center;
        this->y_center = y_center;
    
    
    vector<double> randPoint() 
        double x, y;
        while (true) 
            x = rand(-radius, radius);
            y = rand(-radius, radius);
            if (sqrt(x * x + y * y) <= radius) 
                break;
            
        
        return x + x_center, y + y_center;
    
;

方法二：直接在圆里rand

方法一虽然简单，但是有可能产生不在范围内的数据。因此这种方法就是直接生成圆内的点的。

这让人很容易想到使用极坐标的方法来随机圆内的点。极坐标的方法是随机一个半径$r$，然后随机一个角度$degree$（$[0,2\pi )$）。

那么这个点就是$(x\_center+r\ast cos(degree),y\_center+r\ast sin(degree))$

易错误区

半径$r$如何rand呢？直接r = rand(0, radius)在[0, radius]范围内线性随机取值？

那么这样求出来的结果就不够随机。所有的点会更集中于圆心。

我们来模拟一下这种随机方式：

上图中我们模拟了线性随机rand半径（也就是说，每种长度的半径是等概率的。上图每个红色圆的半径呈等差数列）

然后我们随机rand角度：

角度也是等可能rand的，上图蓝色线表示角度，每两条相邻蓝线之间的角度差值相同。

这样，蓝线与红线相交的点就是采用这种方式随机出来的点。

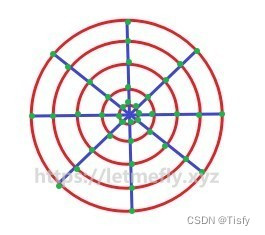
只看绿色的点（采用上述方式随机出来的点），不难发现半径越小密度越大（也就是说有更大概率点会落在距离圆心很近的位置）。

那么我们如何随机半径呢？

我们可以rand这个点所在同心圆的面积。

也就是说，我们不直接rand半径，而是rand面积。

再通过面积求得半径。这样随机出来的点才是真正随机的。

但是具体证明需要用到“概率密度函数 PDF”和“累积分布函数 CDF”，这里蒟蒻就不证明了😶。有兴趣的同学可以参考力扣官方题解的方法二。

• 时间复杂度$O(1)$
• 空间复杂度$O(1)$

AC代码

C++

const double PI = acos(-1);

inline double rand(double l, double r) 
    return (double)1 * rand() * (r - l) / RAND_MAX + l;


inline double rand(double r) 
    return rand(0, r);


class Solution 
private:
    double radius;
    double x_center;
    double y_center;
public:
    Solution(double radius, double x_center, double y_center) 
        srand(time(NULL));
        this->radius = radius;
        this->x_center = x_center;
        this->y_center = y_center;
    
    
    vector<double> randPoint() 
        double area = rand(PI * radius * radius);  // 随机面积
        double r = sqrt(area / PI);  // 根据面积求半径
        double degree = rand(PI * 2);  // 随机角度
        return x_center + r * cos(degree), y_center + r * sin(degree);
    
;

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/125129132