Bayesian statistics

Posted 2023-02-21 yuliured

三种估计的比较
我们假设我们观察的变量是x，观察的变量取值（样本）为D=x_1,…,x_N ，要估计的参数是θ，x的分布函数是p(x┤|θ)

最大似然估计 Maximum Likelihood (ML)

“似然”的意思就是“事情（即观察数据）发生的可能性”，最大似然估计就是要找到θ的一个估计值，使“事情发生的可能性”最大，也就是使p(D|θ)最大。一般来说，我们认为多次取样得到的x是独立同分布的（iid），这样:

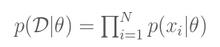
由于P(x_i)一般都比较小，且N一般都比较大，因此连乘容易造成浮点运算下溢，所以通常我们都去最大化对应的对数形式

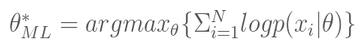
具体求解时，可对右式对θ求导数，然后令为0，求出θ值即为θ_ML^*。

最大似然估计属于点估计，只能得到待估计参数的一个值。

贝叶斯估计 Bayes
使用Bayes公式，我们可以把我们关于θ的先验知识以及在观察数据结合起来，用以确定θ的后验概率p(θ|D)： p(θ|D)=1/Z_D P(D│θ)P(θ)

贝叶斯估计 Bayes
使用Bayes公式，我们可以把我们关于θ的先验知识以及在观察数据结合起来，用以确定θ的后验概率p(θ|D)： p(θ|D)=1/Z_D P(D│θ)P(θ)
其中 是累积因子，以保证p(θ|D)和为1。要使用Bayes方法，我们需有关于θ的先验知识，即不同取值的概率P(θ)。比如θ=1表示下雨，θ=0表示不下雨，根据以往的经验我们大体上有 P(θ=1)=0.01、 P(θ=0)=0.09，在这种知识不足的时候，可以假设θ是均匀分布的，即取各值的概率相等。
在某个确定的θ取值下，事件x的概率就是p(x|θ)，这是关于θ的函数，比如一元正态分布 。与上一节中的一样，我们认为各次取样是独立的，P(D│θ)可以分开来写，这样我们就可以得到p(θ|D)的一个表达式，不同的θ对应不同的值。

根据获得的p(θ|D)，我们边可以取使其最大化的那个θ取值，记为θ_B^*。

问题：做了很多额外工，为了求得一个θ_B^*，我们把θ取其它值的情况也考虑了。

我们只要那个θ_B^*。最大后验估计这个时候就上场了。

最大后验估计 MAP
并不去求解p(θ|D)，而是直接获得θ_B^*。从贝叶斯估计的公式可以看出，Z_D是与θ无关的，要求得使P(θ|D)最的的θ，等价于求解下面的式子：
θ_AMP^*=argmax_θ p(θ│x)=argmax_θ p(x│θ)p(θ)


最大化对应的对数形式：
θ_AMP^*=argmax_θ logp(x│θ)+logp(θ)
这样，我们便无需去计算Z_D，也不需要求得具体的P(θ|D)部分，便可以得到想要的θ_AMP^*。

最大似然估计和Bayes/MAP有很大的不同，原因在于后两种估计方法利用了先验知识p(\\theta)，如果利用恰当，可以得到更好的结果。其实这也是两大派别（Frequentists and Bayesians)的一个区别。