求一些数列的名称及相关知识。 如:Catalan数列，斐波那契数列等。 谢谢！！！

Posted 2023-05-16

catalan数列
卡特兰数原理：令h(1)＝1，catalan数满足递归式： h(n)= h(0)*h(n-1) + h(1)*h(n-2) + ... + h(n-1)h(0) (其中n>=2) 整理得： h(n) = (4*n-2)/(n+1)*h(n-1), n=2,3,... 该递推关系的解为： h(n)=c(2n,n)/(n+1) ，n=1,2,3,...

详细资料见：http://baike.baidu.com/view/1396146.html?wtp=tt

斐波那契数列

详细资料见：http://baike.baidu.com/view/816.html?wtp=tt 参考技术A 上网查一下大把的资料

卡特兰数相关问题

一、什么是Catalan数

说到Catalan数，就不得不提及Catalan序列，Catalan序列是一个整数序列，其通项公式是

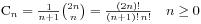
递推公式是

C(n) = C(1)*C(n-1) + C(2)*C(n-2) + ... + C(n-1)C(1)，n>=2

我们从中取出的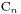就叫做第n个Catalan数，前几个Catalan数如下：

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …

咋看之下没什么特别的，但是Catalan数却是许多计数问题的最终形式。

 

二、Catalan数在组合计算中的应用

1、矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，有几种括号化的方案？

2、一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?

3、n个节点构成的二叉树，共有多少种情形？

4、求一个凸多边形区域划分成三角形区域的方法数？

5、在圆上选择2n个点，将这些点成对链接起来使得所得到的n条线段不相交，一共有多少种方法？(下图供参考)

6、n*n的方格地图中，从一个角到另外一个角，不跨越对角线的路径数为h(n).例如， 4×4方格地图中的路径有：

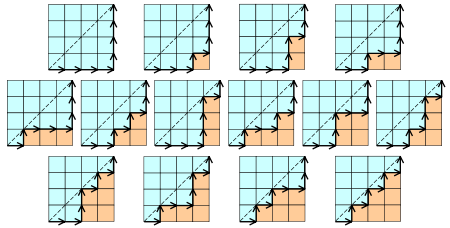
7、n层的阶梯切割为n个矩形的切法数也是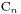。如下图所示：

8、有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？

9、甲乙两人比赛乒乓球，最后结果为20∶20，问比赛过程中甲始终领先乙的计分情形的种数。

10、2n个高矮不同的人，排成两排，每排必须是从矮到高排列，而且第二排比对应的第一排的人高，问排列方式有多少种？

 

以上题目的最终解均与卡特兰数相关，具体的求解分析见“参考资料”。

 

参考资料：

从《编程之美》买票找零问题说起，娓娓道来卡特兰数——兼爬坑指南