[leetcode] 798 得分最高的最小轮调 - 思维dp

Posted 2022-03-12 PushyTao

题目链接

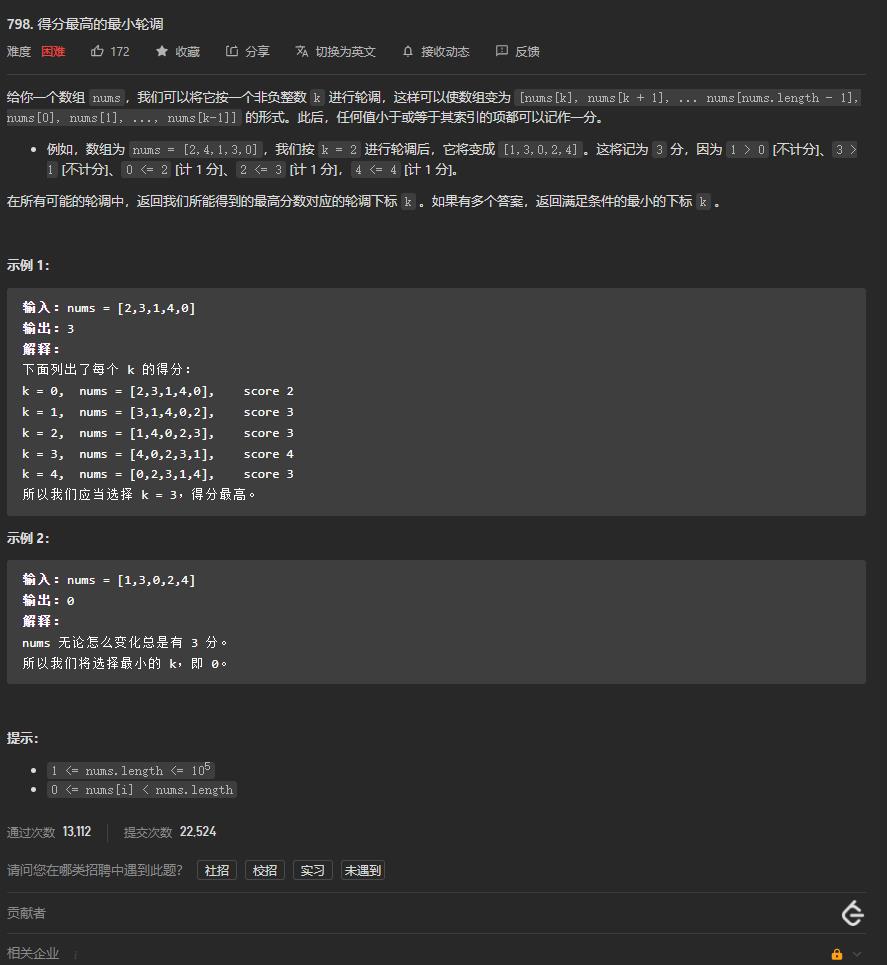
轮调实际上是这个样子的：
每次讲最前面的元素放到数组最后，然后将所有元素集体向前移动一位
在当前值$a[i]\le i$的时候会获得$1$分，问最大的的分是多少?
先说明一个事实：
一次轮调之后，对于除了最前面的每个数，他的下标会减小$1$，而对于最前面的那个数，他的下标直接变为最大
大致分为以下三种情况：

1. 本来$a[i]$就小于下标$i$，轮调之后下标减小值不变，所以依旧会获得$1$分
2. 本来$a[i]==i$，轮调之后，下标减小而值不变，所以值就比下标大$1$，所以说会失去$1$分
3. 本来$a[i]>i$，轮调之后，下标更小，值依旧会大于下标，所以依旧不得分
4. 在最前面的数，一次轮调之后，被放到最大的下标的位置，会得到$1$分

我们用$dp[i]$表示在第$i$次轮调之后会得到的分数，那么就有：
$dp[i]=dp[i-1]-x+1$
其中，$x$表示$i-1$次轮调时下标和值相等的个数
在这里$x$可以预处理得到

式中的 $+1$是为了解决数组最前面的数到数组最后的最大下标处的贡献值
$dp[0]=未轮调的时候的得分$
因为之和前一个关系有关，所以我们可以只用一个变量解决，记录最大值处的下标返回即可

Code:

class Solution 
public:
    int bestRotation(vector<int>& nums) 
        int val = 0;
        const int n = nums.size();
        int a[n+1],pos = 0;
        memset(a,0,sizeof a);
        for(int i = 0; i < n;i ++) 
            if(nums[i] <= i) val ++;
        
        int mxval = val;
        for(int i = 0; i < n;i ++) 
            if(i >= nums[i]) a[i-nums[i]] ++;
            else a[i + n - nums[i]] ++;
        
        
        for(int i=1;i<n;i++) 
            val = val - a[i-1] + 1;
            if(val > mxval) 
                val = mxval;
                pos = i;
            
        
        return pos;
    
;