主成分回归的一般步骤是怎样的

Posted 2023-05-11

原文：http://tecdat.cn/?p=2655

 

此示例显示如何在matlab中应用偏最小二乘回归（PLSR）和主成分回归（PCR），并讨论这两种方法的有效性。当存在大量预测变量时，PLSR和PCR都是对因变量建模的方法，并且这些预测变量高度相关或甚至共线性。两种方法都将新的预测变量（称为成分）构建为原始预测变量的线性组合，但它们以不同的方式构造这些成分。PCR创建成分来解释预测变量中观察到的变异性，而根本不考虑因变量。另一方面，PLSR确实将因变量考虑在内，因此通常会导致模型能够使用更少的成分来适应因变量。

加载数据

加载包括401个波长的60个汽油样品的光谱强度及其辛烷值的数据集。

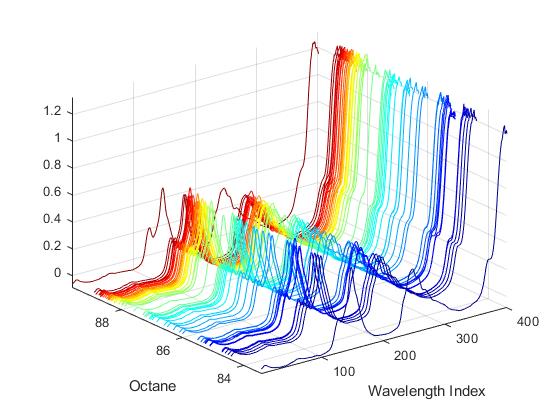
使用两个拟合数据

使PLSR模型拟合10个PLS成分和一个因变量。

为了充分拟合数据，可能需要十个成分，但可以使用此拟合的诊断来选择具有更少成分的更简单模型。例如，选择成分数量的一种快速方法是将因变量中解释的方差百分比绘制为成分数量的函数。

在实践中，在选择成分数量时可能需要更加谨慎。例如，交叉验证是一种广泛使用的方法，稍后将在本示例中进行说明。目前，上图显示具有两个成分的PLSR解释了观察到的大部分方差y。计算双组分模型的拟合因变量。

接下来，拟合具有两个主要成分的PCR模型。第一步是X使用该pca函数执行主成分分析，并保留两个主成分。然后，PCR只是这两个成分的因变量的线性回归。当变量具有非常不同的可变性时，通常首先通过其标准偏差来规范每个变量。

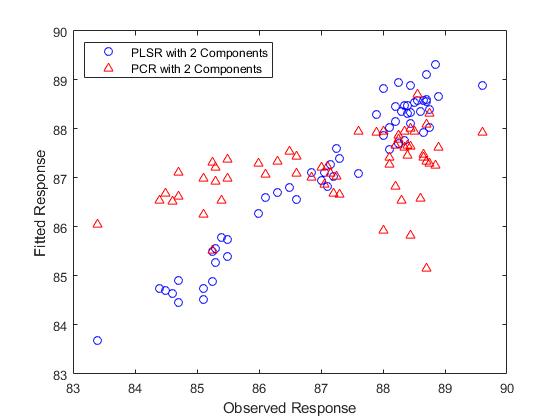
从某种意义上说，上图中的比较并不合理 - 通过观察双组分PLSR模型预测因变量的程度来选择成分数（两个），并且没有说明为什么PCR模型应该限制相同数量的成分。然而，使用相同数量的成分，PLSR做得更好。实际上，观察上图中拟合值的水平分布，使用两个分量的PCR几乎不比使用常数模型好。回归的r方值证实了这一点。

比较两种模型的预测能力的另一种方法是在两种情况下将因变量绘制成两个预测变量。

如果不能以交互方式旋转图形，有点难以看到，但上面的PLSR图显示了紧密分散在平面上的点。另一方面，下面的PCR图显示点几乎没有线性关系。

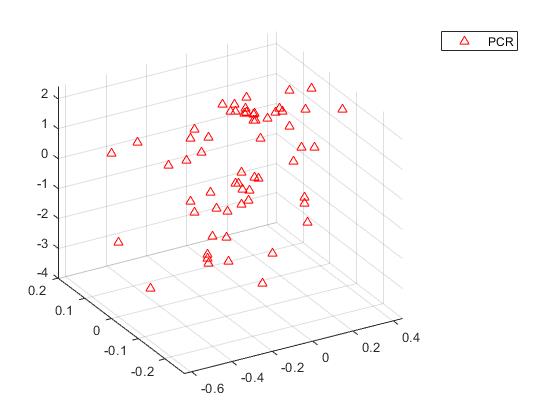
请注意，尽管两个PLS成分是观察到的更好的预测因子，但下图显示它们解释的方差比例比PCR中使用的前两个主成分少。

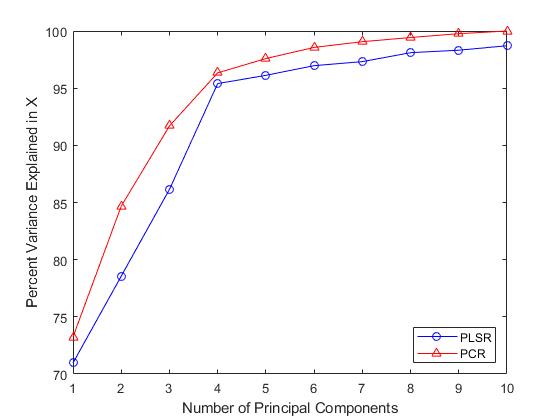
PCR曲线一致性较高的事实表明，为什么使用两种成分的PCR相对于PLSR在拟合时表现很差。PCR构建成分以便最好地解释X，因此，前两个成分忽略了数据拟合中观察到的重要信息y。

拟合更多成分

随着在PCR中添加更多成分，它必然会更好地拟合原始数据y，这仅仅是因为在某些时候，大多数重要的预测信息X将存在于主要成分中。例如，使用10个成分时，两种方法的残差远小于两个成分的残差。

交叉验证

在预测未来变量的观察结果时，选择成分数量以减少预期误差通常很有用。简单地使用大量成分将很好地拟合当前观察到的数据，但这是一种导致过度拟合的策略。过于拟合当前数据会导致模型不能很好地推广到其他数据，并对预期误差给出过度乐观的估计。

交叉验证是一种更加统计上合理的方法，用于选择PLSR或PCR中的成分数量。它通过不重复使用相同的数据来拟合模型和估计预测误差来避免过度拟合数据。因此，预测误差的估计不会乐观地向下偏差。

pls可以选择通过交叉验证来估计均方预测误差（MSEP），在这种情况下使用10倍CV。

plsreg（X，y，10，'CV'，10）;

对于PCR，crossval结合用于计算PCR的平方误差之和，可以再次使用10倍交叉验证来估计MSEP。

sum（crossval（@ pcrsse，X，y，'KFold'，10），1）/ n;

PLSR的MSEP曲线表明两个或三个成分好。另一方面，PCR需要四个成分才能获得相同的预测精度。

事实上，PCR中的第二个成分会增加模型的预测误差，这表明该成分中包含的预测变量的组合与其没有很强的相关性y。再次，这是因为PCR构建成分来解释X，而不是y。

模型简约

因此，如果PCR需要四个成分来获得与具有三个成分的PLSR相同的预测精度，那么PLSR模型是否更加简约？这取决于您考虑的模型的哪个方面。

PLS权重是定义PLS分量的原始变量的线性组合，即，它们描述了PLSR中的每个分量依赖于原始变量的权重。

类似地，PCA载荷描述了PCR中每个成分依赖于原始变量的强度。

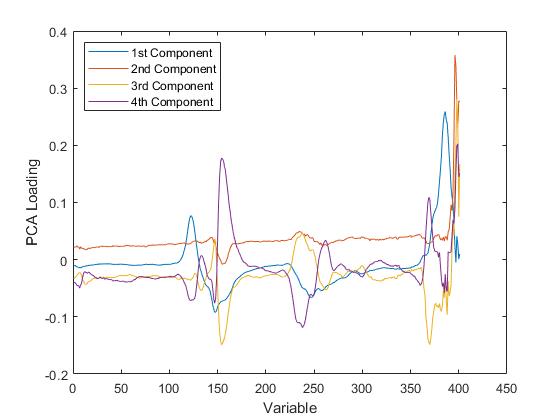
对于PLSR或PCR，可以通过检查每个成分最重要的变量来为每个成分提供有意义的解释。例如，利用这些光谱数据，可以根据汽油中存在的化合物解释强度峰值，然后观察特定成分的权重挑选出少量这些化合物。从这个角度来看，更少的成分更易于解释，并且由于PLSR通常需要更少的成分来充分预测因变量，因此会导致更简约的模型。

另一方面，PLSR和PCR都导致每个原始预测变量的一个回归系数加上截距。从这个意义上讲，两者都不是更简约，因为无论使用多少成分，两种模型都依赖于所有预测变量。更具体地，对于这些数据，两个模型都需要401个光谱强度值以进行预测。

然而，最终目标可能是将原始变量集减少到仍然能够准确预测因变量的较小子集。例如，可以使用PLS权重或PCA载荷来仅选择对每个成分贡献最大的那些变量。如前所示，来自PCR模型拟合的一些成分可主要用于描述预测变量的变化，并且可包括与因变量不强相关的变量的权重。因此，PCR会导致保留预测不必要的变量。

对于本例中使用的数据，PLSR和PCR所需的成分数量之间的差异不是很大，PLS权重和PCA载荷选择了相同的变量。其他数据可能并非如此。

 

有问题欢迎下方留言！

参考文献

1.matlab使用经验模式分解emd 对信号进行去噪

2.Matlab使用Hampel滤波去除异常值

3.matlab偏最小二乘回归(PLSR)和主成分回归(PCR)

4.matlab预测ARMA-GARCH 条件均值和方差模型

5.matlab中使用VMD(变分模态分解) 

6.matlab使用贝叶斯优化的深度学习

7.matlab贝叶斯隐马尔可夫hmm模型

8.matlab中的隐马尔可夫模型(HMM)实现

9.matlab实现MCMC的马尔可夫切换ARMA – GARCH模型

参考技术A 你还是先弄懂什么叫做句子成分，想想汉语的句子成分是什么吧。就像我们把树分成树干、树枝，树叶、树根，这几大部分，你说是按什么步骤分的呢？
所谓句子成分莫非就是讲一件事情比如：“某某人 他干了什么 怎么干的 在哪里干的 结果再怎么样”，或者就是描述人或者事物的状态，比如：“什么东西或者某个人、是什么样子或者怎么样”。行为的主题是主语 动作行为是谓语 动作行为的承受着是宾语，其它的什么样子的、结果怎么样、 在哪里之类的都是补充说明的成分，包括状语，补语，定语。本回答被提问者采纳

Python数据分析案例22——财经新闻可信度分析(线性回归，主成分回归，随机森林回归)

 本次案例还是适合人文社科领域，金融或者新闻专业。本科生做线性回归和主成分回归就够了，研究生还可以加随机森林回归，其方法足够人文社科领域的硕士毕业论文了。

---

案例背景

有八个自变量，['微博平台可信度','专业性','可信赖性','转发量','微博内容质量','时效性','验证程度','人际信任']   ，一个因变量： 投资信息可信度。

研究这八个自变量对因变量的影响。

---

数据读取

导入包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns
from sklearn.preprocessing import StandardScaler
import statsmodels.formula.api as smf
plt.rcParams ['font.sans-serif'] ='SimHei'               #显示中文
plt.rcParams ['axes.unicode_minus']=False               #显示负号
sns.set_style("darkgrid","font.sans-serif":['KaiTi', 'Arial'])

读取，我数据格式这里是spss 的sav格式，但是python也能读取。

# 读取数据清洗后的数据
spss = pd.read_spss('数据2.sav')
#spss

选取需要的变量，展示前五行

data=spss[['微博平台可信','专业性','可信赖性','转发量','微博内容质量','时效性','验证程度','人际信任','投资信息可信度']]
data.head()

取出列名称

columns1=data.columns

描述性统计，算一下均值方差分位数等等

data.describe()  #描述性统计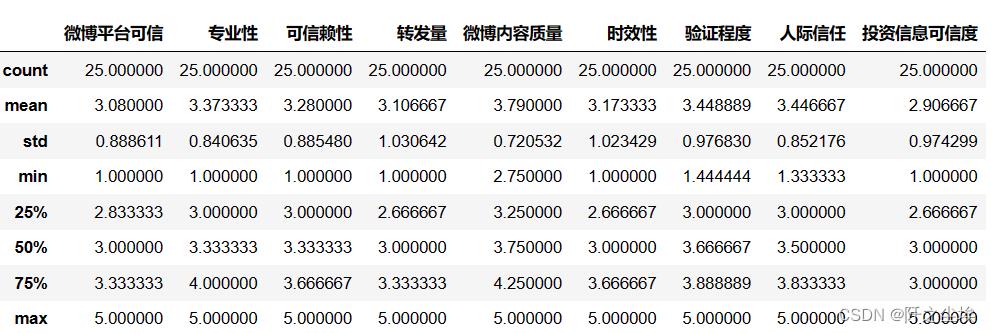

我这数据量并不多.... 

取出X和y

X=data.iloc[:,:-1]
y=data.iloc[:,-1]

 

---

画图展示

对八个自变量和一个因变量画箱线图 

column = data.columns.tolist() # 列表头
fig = plt.figure(figsize=(10,10), dpi=128)  # 指定绘图对象宽度和高度
for i in range(9):
    plt.subplot(3,3, i + 1)  # 2行3列子图
    sns.boxplot(data=data[column[i]], orient="v",width=0.5)  # 箱式图
    plt.ylabel(column[i], fontsize=16)
plt.tight_layout()
plt.show()

 

画核密度图

column = data.columns.tolist() # 列表头
fig = plt.figure(figsize=(10,10), dpi=128)  # 指定绘图对象宽度和高度
for i in range(9):
    plt.subplot(3,3, i + 1)  # 2行3列子图
    sns.kdeplot(data=data[column[i]],color='blue',shade= True)  
    plt.ylabel(column[i], fontsize=16)
plt.tight_layout()
plt.show()

 变量两两之间的散点图

sns.pairplot(data[column],diag_kind='kde')
#plt.savefig('散点图.jpg',dpi=256)

 变量之间的相关系数热力图

#画皮尔逊相关系数热力图
corr = plt.subplots(figsize = (14,14))
corr= sns.heatmap(data[column].corr(),annot=True,square=True)

 可以看到很多x之间的相关系数都挺高的，线性回归模型应该存在严重的多重共线性。

---

线性回归分析

导入包

import statsmodels.formula.api as smf

打印回归方程

all_columns = "+".join(data.columns[:-1])
print('x是：'+all_columns)
formula = '投资信息可信度~' + all_columns
print('回归方程为：'+formula)

拟合模型 

results = smf.ols(formula, data=data).fit()
results.summary()

 

 可以看到拟合优度还挺高，84%。再看每个变量的p值，0.05的显著性水平下，几乎都不显著.....

应该是多重共线性导致的。

还可以这样查看回归结果：

print(results.summary().tables[1])

系数p值什么的和上面一样。

对数回归 

在计量经济学里面有一种常用的手段就是将数据去对数，这样可以减小异方差等影响。我们来试试，取了对数再回归：

data_log=pd.DataFrame(columns=columns1)
for i in columns1:
    data_log[i]=data[i].apply(np.log)

拟合

results_log = smf.ols(formula, data=data_log).fit()
results_log.summary()

 也好不到哪去....只有时效性的p值小于0.05，是显著的，别的都不显著。

接下来使用主成分回归

---

主成分回归

主成分回归会压缩你的变量，弄出几个新的变量，这样变量之间的多重共线性就能处理掉了。

新的变量就是老变量的线性组合，但是不好解释，失去了经济或者新闻上的实际意义。

导包

from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import LeaveOneOut
from mpl_toolkits import mplot3d

想找一下几个主成分回归，要用几个主成分会好一些：

model = PCA()
model.fit(X)
#每个主成分能解释的方差
model.explained_variance_
#每个主成分能解释的方差的百分比
model.explained_variance_ratio_
#可视化
plt.plot(model.explained_variance_ratio_.cumsum(), 'o-')
plt.xlabel('Principal Component')
plt.ylabel('Cumulative Proportion of Variance Explained')
plt.axhline(0.9, color='k', linestyle='--', linewidth=1)
plt.title('Cumulative PVE')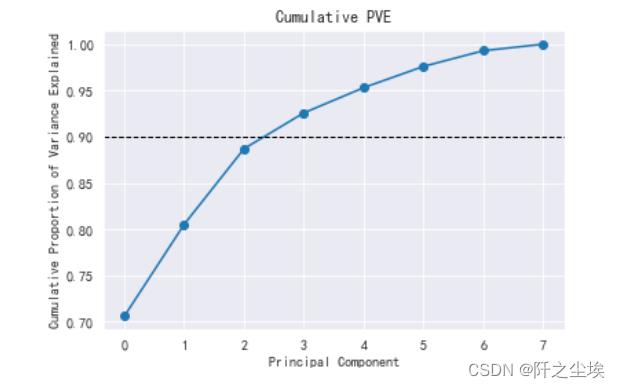

可以看到当主成分个数为4时就能解释原始数据的90%以上了（坐标轴上是3是因为从0 开始的..）

 下面采用四个主成分进行回归分析：

将X转化为4个主成分矩阵，查看数据形状。

model = PCA(n_components = 4)
model.fit(X)
X_train_pca = model.transform(X)
X_train_pca.shape

 

25是我的样本量，4是主成分个数。（25个确实少了....） 

 变成数据框：（主成分得分矩阵）

columns = ['PC' + str(i) for i in range(1, 5)]
X_train_pca_df = pd.DataFrame(X_train_pca, columns=columns)
X_train_pca_df.head()

上面只展示了前5行。

还可以计算主成分核载矩阵，显示了原始变量和主成分之间的关系。

pca_loadings= pd.DataFrame(model.components_.T, columns=columns,index=columns1[:-1])
pca_loadings

 

 打印主成分回归方程

X_train_pca_df['财经信息可信度']=y
all_columns = "+".join(X_train_pca_df.columns[:-1])
print('x是：'+all_columns)
formula = '财经信息可信度~' + all_columns
print('回归方程为：'+formula)

拟合模型

results = smf.ols(formula, data=X_train_pca_df).fit()
results.summary()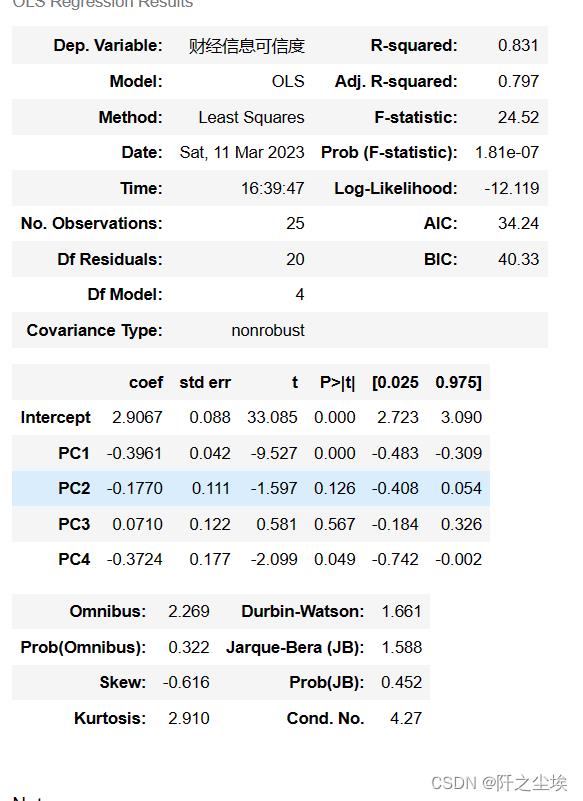

 

 只有第一个和第四个主成分是显著的。

打印查看：

print(results.summary().tables[1])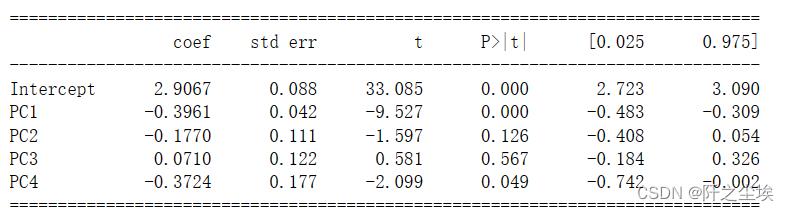

 主成分回归效果也一般。

这种传统的统计学模型——参数模型，线性模型，限制和假定太多了，不好用。

一遇见多重共线性，异方差等问题就G了

 下面采用非参数的回归方法——随机森林，可以避免多重共线性的影响，得到变量的重要特征排序。

---

 

随机森林回归

像随机森林，支持向量机，梯度提升这种机器学习模型放在人文社科领域都是降维打击。人文社科领域用的还是老一套的传统统计学模型，效果都不太好。

随机森林回归在统计、计算机等学科里面都是很简单的模型了，但若在人文社科学科，这种模型写在论文里面肯定算高级的了。

先将数据标准化

# 数据标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(data)
data = scaler.transform(data)
data[:5]

 取出X和y

airline_scale = data
airline_scale.shape

X=airline_scale[:,:-1]
y=airline_scale[:,-1]
X.shape,y.shape

 拟合模型：

from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=5000, max_features=int(X.shape[1] / 3), random_state=0)
model.fit(X,y)
model.score(X,y)

上面这段代码生成了一个含有5000棵决策树的随机森林模型，拟合，评价。

拟合优度高达95%！！ 

查看真实值和拟合值对比的图：

pred = model.predict(X)
plt.scatter(pred, y, alpha=0.6)
w = np.linspace(min(pred), max(pred), 100)
plt.plot(w, w)
plt.xlabel('pred')
plt.ylabel('y_test')
plt.title('模型预测的财经信息可信度和真实值对比')

 

 很接近。

计算变量的重要性：

model.feature_importances_
sorted_index = model.feature_importances_.argsort()

plt.barh(range(X.shape[1]), model.feature_importances_[sorted_index])
plt.yticks(np.arange(X.shape[1]), columns1[:-1][sorted_index],fontsize=14)
plt.xlabel('Feature Importance',fontsize=14)
plt.ylabel('Feature')
plt.title('特征变量的重要性排序图',fontsize=24)
plt.tight_layout()

可以看到，对于 投资信息可信度这样因变量，信息的时效性，转发量，平台可信度是最重要的，其次就是人际信任，可信赖性等等变量。

上面是每个变量对于y的重要性，

下面画出每个变量分别是怎么影响y的，偏依赖图：

X2=pd.DataFrame(X,columns=columns1[:-1])
from sklearn.inspection import PartialDependenceDisplay
#plt.figure(figsize=(12,12),dpi=100)
PartialDependenceDisplay.from_estimator(model, X2,['时效性','转发量','微博平台可信'])
#画出偏依赖图

我们可以很清楚得看到，时效性，转发量，微博平台可信度，三个变量的取值变化是怎么影响y的变化的，明显不是一个线性的关系，虽然大致的方向是正相关，但是影响的程度是一个非线性的关系，先慢后快再慢。

---

总结 

本次用了三种方法做了一个财经新闻领域的回归问题，每个方法都有优缺点吧，但是效果肯定还是机器学习的模型好。有的同学肯定在想机器学习模型怎么没有p值什么的，怎么看显不显著？

其实机器学习的方法没有参数估计和假设检验的，没有p值什么的，所以做不了统计推断，这也是它的一个缺点。传统的线性回归，主成分回归，虽然可以统计推断，但是效果很差。

看每个人的需求做什么样的模型了，但是在人文社科的论文写一歌机器学习的模型还是算得上创新吧。