线性回归实战房价预测

Posted 2022-02-20 辰chen

前言

本文属于 线性回归算法【AIoT阶段三】（尚未更新），这里截取自其中一段内容，方便读者理解和根据需求快速阅读。本文通过公式推导+代码两个方面同时进行，因为涉及到代码的编译运行，如果你没有 $NumPy$，$Pandas$，$Matplotlib$ 的基础，建议先修文章：数据分析三剑客【AIoT阶段一（下）】（十万字博文 保姆级讲解）

线性回归预测房价

1.数据加载

首先导包：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression

我们要实现的是对 波士顿 这个城市进行房价预测，有关 波士顿 的数据，可以直接用代码：

boston = datasets.load_boston()

我们来看一下 datasets.load_boston() 里面都有哪些数据：

数据由三部分组成：

• $data$ 即数据，这些数据影响了房价，统计指标
• $target$ 指房价，$24$ 就表示 $24$ 万美金
• $feature\_names$ 就是具体的指标，比如 $CRIM$：犯罪率；$NOX$：空气污染，$N$元素的含量；$TAX$ ：税收；这些指标都会影响到房价

我们把这些信息分开来处理：

boston = datasets.load_boston()

X = boston['data']   # 数据,这些数据影响了房价,统计指标
y = boston['target'] # 房价,24就表示24万美金

# CRIM:犯罪率
# NOX:空气污染,N含量
# TAX:税收
# 这些指标都和放假有关
feature_names = boston['feature_names'] # 具体指标

2.数据查看

# 506 表示 506 个统计样本
# 13 表示影响房价的 13 个属性
X.shape

# 506 个房子
# X -----> y 是一一对应的
# 数据 -----> 目标值对应
y.shape

3.数据拆分

# 506个数据、样本
# 拆分成两份：一份 80%用于训练，一份20%用于验证
# 拿出其中的80%，交给算法(线性回归)，去进行学习、总结、拟合函数
# 20%作用：验证，测一测，看看算法，学习80%结束，是否准确
# 如何划分：利用 numpy 的 shuffle 打乱数据
index = np.arange(506)
np.random.shuffle(index)
index

$506\times 80\%\approx 405$，故我们拿出打乱后的前 $405$ 个数据用于训练算法，其余数据用于验证算法：

# 80% 训练数据
train_index = index[:405]
X_train = X[train_index]
y_train = y[train_index]
# 20% 测试数据
test_index = index[405:]
X_test = X[test_index]
y_test = y[test_index]

4.数据建模

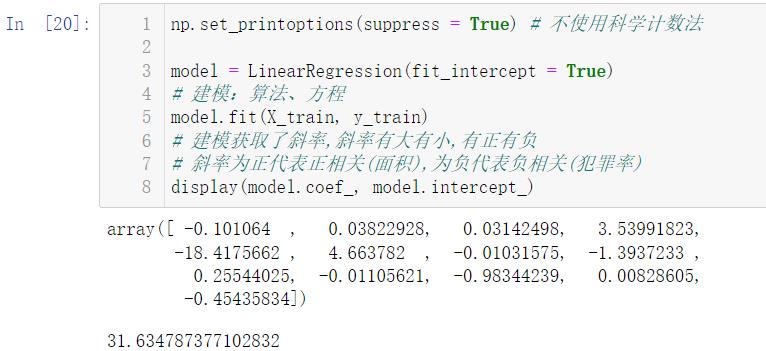
np.set_printoptions(suppress = True) # 不使用科学计数法

model = LinearRegression(fit_intercept = True)
# 建模：算法、方程
model.fit(X_train, y_train)
# 建模获取了斜率,斜率有大有小,有正有负
# 斜率为正代表正相关(面积),为负代表负相关(犯罪率)
display(model.coef_, model.intercept_)

5.模型验证

# 模型预测的结果：y_
y_ = model.predict(X_test).round(2)
# 展示前 30 个:
display(y_[:30])
# 展示真实结果的前 30 个:
display(y_test[:30])

算法的预测难免会有异常值，这是 不可避免的！

6.模型评估

# 最大值是 1,最小值可以小于 0
# 这个指标越接近 1,说明算法越优秀
model.score(X_test, y_test)

# 再来判断一下训练数据的得分
model.score(X_train, y_train)

显然，训练数据的得分是高的，这就好比我们在考试前都会做模拟题，我们如果考试卷的大部分题目都和模拟题是一样的，那么我们的分数就会高一些，如果考试的题目都是新题，那么我们的分数就会低一些

当然，我们评测数据不止这一个方法，下面简单介绍一下别的方法：

# 最小二乘法
from sklearn.metrics import mean_squared_error

# 这个是测试数据，对应的是 20%
y_pred = model.predict(X_test)
y_true = y_test
mean_squared_error(y_true, y_pred)

我们再来看那 $80\%$ 的训练数据：

# 80% 的训练数据:
mean_squared_error(y_train, model.predict(X_train))

注意我们这里的分数是 $error$，即 越小越好！