AI数学基础18——常见的正则化方法

Posted 2023-05-10

参考技术A 1，L2 regularization（权重衰减） L2正则化就是在代价函数后面再加上一个正则化项λ ，使得权重在更新的时候，乘以一个小于1的因子（1-a(λ/m))，这个可以防止W过大。正则化项里面有一个系数1/2，1/2经常会看到，主要是为了后面求导的结果方便，后面那一项求导会产生一个2，与1/2相乘刚好凑整。

过拟合的时候，拟合函数的系数往往非常大。过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大

L2 Regularization 防止了系数W过大，也就防止了拟合函数导数值过大，也就防止了函数导数值波动过大，也就解决了过拟合问题。

L2正则化是训练深度学习模型中最常用的一种解决过拟合问题的方法。

2，L1 regularization， L1正则化的正则项是所有权重w的绝对值的和，乘以λ/n（这里不像L2正则化项那样，需要再乘以1/2）；消除过拟合的原因与L2类似。使用频率没有L2正则化高。

3，Dropout正则化

L1、L2正则化是通过修改代价函数来实现的，而Dropout则是通过修改神经网络本身来实现的。

Dropout是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。注意是暂时，对于随机梯度下降来说，由于是随机丢弃，故而每一个mini-batch都在训练不同的网络。

运用了dropout的训练过程，相当于训练了很多个只有半数隐层单元的神经网络（后面简称为“半数网络”），每一个这样的半数网络，都可以给出一个分类结果，这些结果有的是正确的，有的是错误的。随着训练的进行，大部分半数网络都可以给出正确的分类结果，那么少数的错误分类结果就不会对最终结果造成大的影响。

dropout率的选择：经过交叉验证， 隐含节点dropout率等于0.5的时候效果最好 ，原因是0.5的时候dropout随机生成的网络结构最多

具体细节，推荐Alex和Hinton的论文《 ImageNet Classification with Deep Convolutional Neural Networks 》

4，数据集扩增（data augmentation）

在深度学习方法中，更多的训练数据，意味着可以用更深的网络，训练出更好的模型。

但是很多时候，收集更多的数据意味着需要耗费更多的人力物力，非常困难。

所以，可以在原始数据上做些改动，得到更多的数据，以图片数据集举例，可以做各种变换，如：

1，水平翻转或任意角度旋转；2，裁剪；3，添加噪声

更多数据意味着什么？

用50000个MNIST的样本训练SVM得出的accuracy94.48%，用5000个MNIST的样本训练NN得出accuracy为93.24%，所以更多的数据可以使算法表现得更好。在机器学习中，算法本身并不能决出胜负，不能武断地说这些算法谁优谁劣，因为数据对算法性能的影响很大。

5，提前停止训练神经网络（Early Stop）

在一个适中的迭代次数，W不是很大的时候，dev set error接近最小，train set error适中的时候，提前停止训练，如下图所示

参考文献：Andrew Ng《Prractical aspects of Deep learning》1.1~1.8

Python机器学习及实践——进阶篇4（模型正则化之L1正则&L2正则）

正则化的目的在于提高模型在未知测试数据上的泛化力，避免参数过拟合。由上一篇的例子可以看出，2次多项式回归是相对较好的模型假设。之所以出现如4次多项式那样的过拟合情景，是由于4次方项对于的系数过大，或者不为0导致。

因此正则化的常见方法都是在原模型优化目标的基础上，增加对参数的惩罚项。以我们之前在线性回归器一节中介绍过的最小二乘优化目标为例，如果加入对模型的L1范数正则化，那么新的线性回归目标如下式所示：

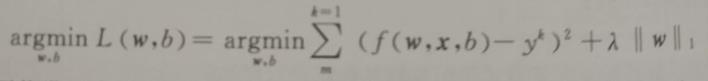
也就是在原优化目标的基础上，增加了参数向量的L1范数。这样在新目标优化的过程中同时需要考量L1惩罚项的影响。为了使目标最小化，这种正则化方法的结果会让参数向量中许多元素趋向于0，使得大部分特征失去对优化目标的贡献。这种让有效特征变得稀疏的L1正则化模型，通常被称为Lasso。

接下来我们用下述代码在上一篇例子的基础上，继续使用4次多项式特征，但是换成Lasso模型检验L1范数正则化后的性能和参数。

# 从sklearn.linear_model中导入Lasso。
from sklearn.linear_model import Lasso

# 从使用默认配置初始化Lasso。
lasso_poly4 = Lasso()
# 从使用Lasso对4次多项式特征进行拟合。
lasso_poly4.fit(X_train_poly4, y_train)

# 对Lasso模型在测试样本上的回归性能进行评估。
print lasso_poly4.score(X_test_poly4, y_test)

0.83889268736

# 输出Lasso模型的参数列表。
print lasso_poly4.coef_

[  0.00000000e+00   0.00000000e+00   1.17900534e-01   5.42646770e-05

-2.23027128e-04]

# 回顾普通4次多项式回归模型过拟合之后的性能。
print regressor_poly4.score(X_test_poly4, y_test)

0.809588079578

# 回顾普通4次多项式回归模型的参数列表。
print regressor_poly4.coef_

[[  0.00000000e+00  -2.51739583e+01   3.68906250e+00  -2.12760417e-01

    4.29687500e-03]

通过对代码一系列输出的观察，验证了我们所介绍的Lasso模型的特点：

1. 相比于普通4次多项式回归模型在测试集上的表现，默认配置的Lasso模型性能提高了大约3%；
2. 相较之下，Lasso模型拟合后的参数列表中，4次与3次特征的参数均为0.0，使得特征更加稀疏。

 

L2范数正则化

与L1范数正则化略有不同的是，L2范数正则化则在原优化目标的基础上，增加了参数向量的L2范数的惩罚项，如下述公式所示。为了使新优化目标最小化，这种正则化方法的结果会让参数向量中的大部分元素都变得很小，压制了参数之间的差异性。这种正则化模型通常被称为Ridge。

我们同样使用代码，继续对4次多项式特征换成Ridge模型检验L2范数正则化后的性能和参数。

# 输出普通4次多项式回归模型的参数列表。
print regressor_poly4.coef_

[[  0.00000000e+00  -2.51739583e+01   3.68906250e+00  -2.12760417e-01

    4.29687500e-03]]

# 输出上述这些参数的平方和，验证参数之间的巨大差异。
print np.sum(regressor_poly4.coef_ ** 2)

647.382645692

# 从sklearn.linear_model导入Ridge。
from sklearn.linear_model import Ridge
# 使用默认配置初始化Riedge。
ridge_poly4 = Ridge()

# 使用Ridge模型对4次多项式特征进行拟合。
ridge_poly4.fit(X_train_poly4, y_train)

# 输出Ridge模型在测试样本上的回归性能。
print ridge_poly4.score(X_test_poly4, y_test)

0.837420175937

# 输出Ridge模型的参数列表，观察参数差异。
print ridge_poly4.coef_

[[ 0.         -0.00492536  0.12439632 -0.00046471 -0.00021205]]

# 计算Ridge模型拟合后参数的平方和。
print np.sum(ridge_poly4.coef_ ** 2)

0.0154989652036

通过对上述输出的观察，可以验证Ridge模型的特点：

1. 相比于普通4次多项式回归模型在测试集上的表现，默认配置的Ridge模型性能提高了近3%；
2. 与普通4次多项式回归模型不同的是，Ridge模型拟合后的参数之间差异非常小。

这里需要指出的是，上面两个公式中的惩罚项，都有一个因子λ进行调节。尽管λ不属于需要拟合的参数，却在模型优化中扮演非常重要的角色。具体对λ的解读，会留在后续。