求matlab周期三角波信号频谱分析的代码，能画出三角波信号、幅度谱和相位谱。

Posted 2023-05-09

%产生峰值为1的三角波，分析其0~63次谐波的幅值谱和相位谱

clf;

Fs =128；%采样频率

T = 1/Fs；% 采样周期

N = 128；% 采样点数

t = (0:N-1)*T；% 时间，单位：S

x=zeros(N);

for n=0:N-1

b=fix((n)/(N/4));

Y=fft(y,512);

F =10*f*[0:256]/512;

fp=2*sqrt(Y.*conj(Y));％幅度谱

xp=angle(Y); ％相位谱

gl=abs(Y).^2; %功率谱

magif=ifft2(abs(f2));%幅度重构

pha=angle(f2);%取相位

phaif=ifft2(exp(j*pha));%相位重构

数据是x(i)，共N个点，采样频率是fsample

扩展资料 ：

信号源有很多种，包括正弦波信号源，函数发生器、脉冲发生器、扫描发生器、任意波形发生器、合成信号源等。一般来讲任意波形发生器，是一种特殊的信号源，综合具有其它信号源波形生成能力，因而适合各种仿真实验的需要。

传统都认为信号源主要给被测电路提供所需要的已知信号（各种波形），然后用其它仪表测量感兴趣的参数。可见信号源在电子实验和测试处理中，并不测量任何参数而是根据使用者的要求，仿真各种测试信号，提供给被测电路，以达到测试的需要。

参考资料来源：百度百科-三角波信号

参考技术A

%产生峰值为1的三角波，分析其0~63次谐波的幅值谱和相位谱

clf;

Fs =128;                   %采样频率

T = 1/Fs;                  % 采样周期

N = 128;                   % 采样点数

t = (0:N-1)*T;             % 时间，单位：S

x=zeros(N);

for n=0:N-1

    b=fix((n)/(N/4));

    m=n+1;

    A=1/(N/4);

    if b==0 

        x(m)=A*n;

    elseif b==1||b==2

        x(m)=A*(N/2-n);

    elseif b==3

        x(m)=A*(n-N);

    end;

end;

n=0:N-1;

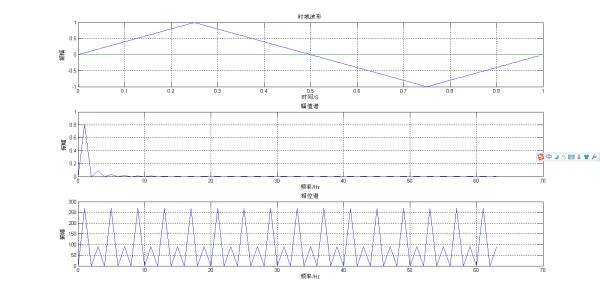
subplot(3,1,1)

plot(t,x);

xlabel('时间/S');

ylabel('振幅');title('时域波形');grid on;

y=fft(x,N);   %对信号进行快速Fourier变换

mag=abs(y)*2/N;   %求取Fourier变换的振幅;*2/N转变为真实幅值

f=n*Fs/N;

subplot(3,1,2)

plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅

xlabel('频率/Hz');

ylabel('振幅');title('幅值谱');grid on;

p=mod(angle(y)*180/pi,360);

subplot(3,1,3)

plot(f(1:N/2),p(1:N/2)); %绘出Nyquist频率之前随频率变化的相位

xlabel('频率/Hz');

ylabel('振幅');title('相位谱');grid on;

本回答被提问者采纳

matlab 作出信号频谱图

先对信号等时间采样得到一组时域信号然后做傅里叶变换。特殊情况下可以看出数据点所满足的解析式，使用拟合，然后对拟合得到的函数进行傅里叶变换，用matlab的fourier函数即可。一般情况下得到的离散的数据点没有明显的拟合函数，这时候可以考虑用离散傅里叶变换。matlab中的fft函数可以完成这个功能。

由于一般情况中的fft更具有应用性，下面着重举例说明fft。

引用一段matlab帮助文件提供的代码作说明：（%后面是中文或英文注释）

clc;clear;

Fs = 1000;                    % Sampling frequency，取样频率

T = 1/Fs;                      % Sample time，采样时间间隔

L = 1000;                     % Length of signal，总时间

t = (0:L-1)*T;                % Time vector，时间向量

% Sum of a 50 Hz sinusoid and a 120 Hz sinusoid 信号函数，提供50Hz和120Hz的主频率

x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); 

y = x + 2*randn(size(t));     % Sinusoids plus noise 信号函数加上模拟的噪音

plot(Fs*t(1:100),y(1:100))    % 信号图

title('Signal Corrupted with Zero-Mean Random Noise')

xlabel('time (milliseconds)')

NFFT = 2^nextpow2(L); % Next power of 2 from length of y 扩充采样点，由1000变为1024

Y = fft(y,NFFT)/L;%除一个L，使归一化，可以不除，不影响对主频率的判断

f = Fs/2*linspace(0,1,NFFT/2+1);%这里除以2是因为fft的对称性，因此只画一半

% Plot single-sided amplitude spectrum.

figure

plot(f,2*abs(Y(1:NFFT/2+1))) %乘2是为了归一化，因为右边一半的fft图像没画；不乘，不影响对主频率的判断

title('Single-Sided Amplitude Spectrum of y(t)')

xlabel('Frequency (Hz)')

ylabel('|Y(f)|')

这行代码“f = Fs/2*linspace(0,1,NFFT/2+1);”如果不理解可以写成

“f = Fs*linspace(0,1,NFFT);”然后把后面的plot行的乘2去掉，NFFT/2+1也改成NFFT，这就等于没有折叠的状态。

至于为什么对称、为什么表达式是这样，就需要去做DFT数学推导了，这里不做推导。

得图如下：

折叠了的fft图。在50与120Hz处有明显的主峰。

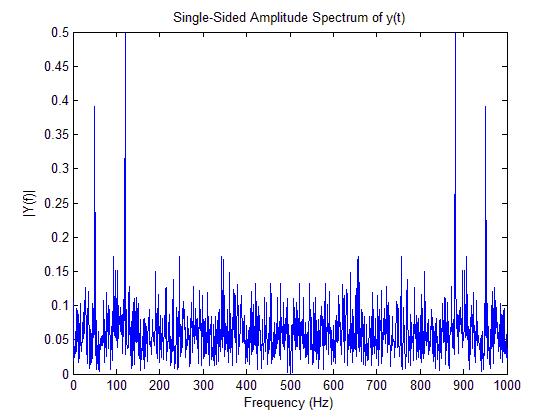
未折叠的fft图。右边两个峰值并没有实际意义，只是由于对称性而得到的。

参考技术A 看看这个————matlab如何做频谱分析% ----------------------------------------------------------------------------------------------------------------
% 方案1：“x = a*cos(2*pi*w*t)”的形式：
% ----------------------------------------------------------------------------------------------------------------
% 注意：1.时域的持续时间范围应较大；
% 2.频率w与序列k的对应关系（N为序列总长度）：w = 1/dt * k/N;
% 3.采样频率1/dt应大于 w 的2倍
% 4.结果曲线的峰值的横坐标对应的就是w和-w值
% ----------------------------------------------------------------------------------------------------------------
a = 0.75;
w = pi/3;
dt = 0.2;
t = [-30*pi:dt:30*pi];
N = size(t, 2);
x = a*cos(2*pi*w*t);
y = fft(x);
y = fftshift(y);
figure;
subplot(2,1,1);
plot(t,x);
subplot(2,1,2);
plot(1/dt*(-N/2+1:N/2)/N, abs(y));

% ----------------------------------------------------------------------------------------------------------------
% 方案2：“x = a*cos(w*t)”的形式：
% ----------------------------------------------------------------------------------------------------------------
% 注意：1.时域的持续时间范围应较大；
% 2.频率w与序列k的对应关系（N为序列总长度）：w = 1/dt *2*pi* k/N;
% 3.采样频率1/dt应大于 w/(2*pi) 的2倍
% 4.结果曲线的峰值的横坐标对应的就是w和-w值
% ----------------------------------------------------------------------------------------------------------------
a = 0.75;
w = pi/3;
dt = 1;
t = [-20*pi:dt:20*pi];
N = size(t, 2);
x = a*cos(w*t);
y = fft(x);
y = fftshift(y);
figure;
subplot(2,1,1);
plot(t,x);
subplot(2,1,2);
plot(1/dt*2*pi*(-N/2:N/2-1)/N, abs(y));

备注：由于使用了fftshift，所以得到的频谱序列关于原点对称，如果不需要负半轴的话自行修改一下就ok了function f=frequency(x,fs)
dtlen=length(x);
t=(0:dtlen-1)/fs;
subplot(211);
plot(t,x);
axis tight;
y=abs(fft(x))*2/dtlen;
ff=(0:dtlen/2-1)*fs/dtlen;
subplot(212);
f=y(1:floor(dtlen/2));
plot(ff,f);
axis tight;
return;