【Matlab的图形绘制和频谱计算】+和+【基本信号的表达式】

Posted 2023-04-18

课程设计要求如下：
在matlab环境下实现基本信号的图形绘制和频谱计算，基本信号包括：正弦信号（sin）、余弦信号（cos）、冲击函数（Diric）、锯齿波或三角波（sawtooth）、方波（square）、sinc函数等、指数函数、矩形脉冲、阶跃信号。

问题如下：
1：在matlab环境下实现基本信号的图形绘制和频谱计算，应该怎么做？过程复杂？有木有相关的文献参考？
2：以下信号的表达式，在信号与系统中分别是怎么写的？正弦信号（sin）、余弦信号（cos）、冲击函数（Diric）、锯齿波或三角波（sawtooth）、方波（square）、sinc函数等、指数函数、矩形脉冲、阶跃信号。

以上问题重点回答问题1，不行的话回答问题2也行。。谢谢大家~

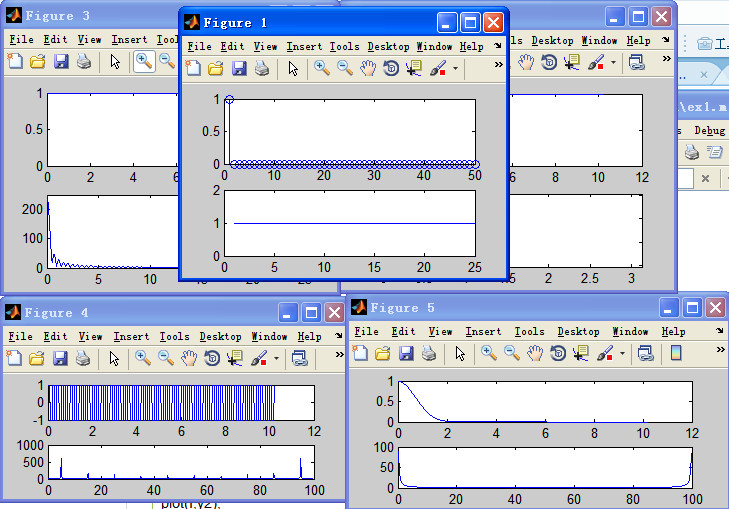
matlab只能做离散数值计算（符号计算只是小部分），所以绘制上述信号图形必须抽样离散化（指定时长，抽样频率等），时域图形可逐点画出，频域要做离散FFT后画出。

根据那奎斯特抽样定理，抽样频率要高于信号中最高频率的两倍，才不会失真，因此频谱中（fs/2,fs）为无用谱，故频域信号的定义域向量与值域向量都应该做减半处理

 

以sin(x)为例：

clear all;   %
N=1024;      %信号的抽样点数
fs=10;       %抽样频率，高于信号中最高频率的2倍
t=(0:N-1)/fs;     
f=(0:N-1)*fs/N;   
x=sin(2*pi.*t); %待处理信号sin(x)=sin(2πft),f=1hz
y=abs(fft(x));     %FFT后求模
f=f(1:N/2);      %减半
y=y(1:N/2);      %减半
subplot(2,1,1)   %画图
plot(t(1:2*fs),x(1:2*fs)); %只画2个周期
subplot(2,1,2)   %画图
plot(f,y);

追问

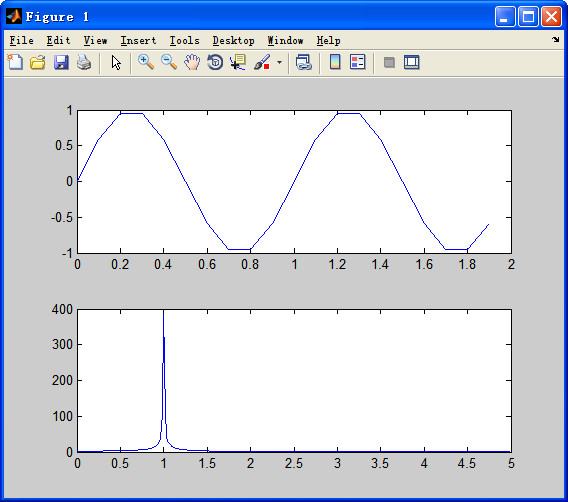
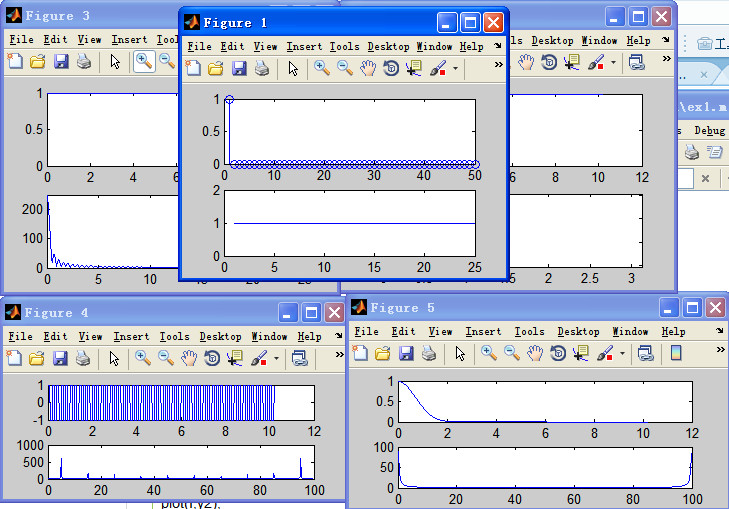
你能不能帮我个忙？帮多少算多少。求下列信号的频谱图，以及代码：1、单位冲击信号 2、方波信号 3、指数信号 4 、单位阶跃信号。【PS】你只要做出两个，这个问题最佳答案给你。做出四个，额外追加最高悬赏！ 救人一命，胜造七级浮屠。希望大家施以援手！！

追答

自己看吧,但愿你能理解,而不是COPY完事

-------------------------------------------------------

clear;
close all;
N=50;
t=1:N;

x=zeros(1,50);
x(1)=1; %单位冲击
figure;
subplot(2,1,1);
stem(x);
X=fft(x);
magX=abs(X); 
subplot(2,1,2);
plot(t(1:N/2),magX(1:N/2));

N=1024;      %信号的抽样点数
fs=100;       %抽样频率，高于信号中最高频率的2倍
t=(0:N-1)/fs;     
f=(0:N-1)*fs/N;   

x0=sign(t); %阶跃
x1=sign(sign(8-t)+1);   %单个方波,宽度为8个采样周期
x2=square(2*pi*5*t,50);  %周期方波,5Hz,50%占空比
x3=exp(-t.^2);

y0=abs(fft(x0));     %FFT后求模
figure;
subplot(2,1,1)
plot(t,x0); 
subplot(2,1,2)
plot(f,y0);

y1=abs(fft(x1));     %FFT后求模
figure;
subplot(2,1,1)   
plot(t,x1); 
subplot(2,1,2)   
plot(f,y1);

y2=abs(fft(x2));
figure;
subplot(2,1,1)   
plot(t,x2); 
subplot(2,1,2)   
plot(f,y2);

y3=abs(fft(x3));   
figure;
subplot(2,1,1) 
plot(t,x3); 
subplot(2,1,2) 
plot(f,y3);

参考技术A 1.矩形脉冲信号：F（w）=2Esin(wt/2)/w
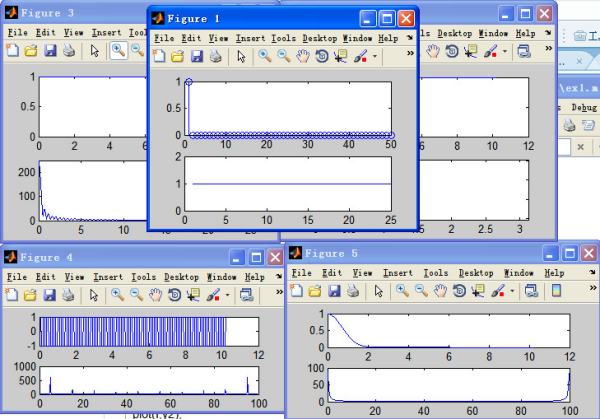
2.钟形信号：f(t)=Ee^(-t/T)^2F(w)
3.三角函数形式:f(t)=a0+a1cos(w1t)+a2cos(2w1t)+...+ancos(nw1t)+b1sin(w1t)+b2shin(2w1t)+..+bnsin(nw1t) 参考技术B 参考参考：

原文地址：matlab绘制三维图形作者：hotinko1
三维曲线
plot3函数与plot函数用法十分相似，其调用格式为：
plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)
其中每一组x,y,z组成一组曲线的坐标参数，选项的定义和plot函数相同。当x,y,z是同维向量时，则x,y,z 对应元素构成一条三维曲线。当x,y,z是同维矩阵时，则以x,y,z对应列元素绘制三维曲线，曲线条数等于矩阵列数。
例 绘制三维曲线。
程序如下：
t=0:pi/100:20*pi;
x=sin(t);
y=cos(t);
z=t.*sin(t).*cos(t);
plot3(x,y,z);
title('Line in 3-D Space');
xlabel('X');ylabel('Y');zlabel('Z');

三维曲面
1．产生三维数据
在MATLAB中，利用meshgrid函数产生平面区域内的网格坐标矩阵。其格式为：
x=a:d1:b; y=c:d2:d;
[X,Y]=meshgrid(x,y);
语句执行后，矩阵X的每一行都是向量x，行数等于向量y的元素的个数，矩阵Y的每一列都是向量y，列数等于向量x的元素的个数。
2．绘制三维曲面的函数
surf函数和mesh函数的调用格式为：
mesh(x,y,z,c)：画网格曲面，将数据点在空间中描出,并连成网格。
surf(x,y,z,c)：画完整曲面，将数据点所表示曲面画出。
一般情况下，x,y,z是维数相同的矩阵。x,y是网格坐标矩阵，z是网格点上的高度矩阵，c用于指定在不同高度下的颜色范围。
例 绘制三维曲面图z=sin(x+sin(y))-x/10。
程序如下：
[x,y]=meshgrid(0:0.25:4*pi); %在[0,4pi]×[0,4pi]区域生成网格坐标
z=sin(x+sin(y))-x/10;
mesh(x,y,z);
axis([0 4*pi 0 4*pi -2.5 1]);
此外，还有带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。其用法与mesh类似，不同的是meshc还在xy平面上绘制曲面在z轴方向的等高线，meshz还在xy平面上绘制曲面的底座。
例 在xy平面内选择区域[-8,8]×[-8,8]，绘制4种三维曲面图。
程序如下：
[x,y]=meshgrid(-8:0.5:8);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);
subplot(2,2,1);
mesh(x,y,z);
title('mesh(x,y,z)')
subplot(2,2,2);
meshc(x,y,z);
title('meshc(x,y,z)')
subplot(2,2,3);
meshz(x,y,z)
title('meshz(x,y,z)')
subplot(2,2,4);
surf(x,y,z);
title('surf(x,y,z)')
3．标准三维曲面
sphere函数的调用格式为：
[x,y,z]=sphere(n)：generates three
(N+1)-by-(N+1) matrices so that SURF(X,Y,Z) produces a unit sphere.
cylinder函数的调用格式为：
[x,y,z]= cylinder(R,n)，其中r为圆周半径，n为组成圆周的点数。
MATLAB还有一个peaks 函数，称为多峰函数，常用于三维曲面的演示。
例 绘制标准三维曲面图形。
程序如下：
t=0:pi/20:2*pi;
[x,y,z]= cylinder(2+sin(t),30);
subplot(2,2,1);
surf(x,y,z);
subplot(2,2,2);
[x,y,z]=sphere;
surf(x,y,z);
subplot(2,1,2);
[x,y,z]=peaks(30);
surf(x,y,z);
其他三维图形
在介绍二维图形时，曾提到条形图、杆图、饼图和填充图等特殊图形，它们还可以以三维形式出现，使用的函数分别是bar3、stem3、pie3 和fill3。
bar3函数绘制三维条形图，常用格式为：
bar3(y)
bar3(x,y)
stem3函数绘制离散序列数据的三维杆图，常用格式为：
stem3(z)
stem3(x,y,z)
pie3函数绘制三维饼图，常用格式为：
pie3(x)
fill3函数等效于三维函数fill，可在三维空间内绘制出填充过的多边形，常用格式为：
fill3(x,y,z,c)
例 绘制三维图形：
(1) 绘制魔方阵的三维条形图。
(2) 以三维杆图形式绘制曲线y=2sin(x)。
(3) 已知x=[2347,1827,2043,3025]，绘制饼图。
(4) 用随机的顶点坐标值画出五个黄色三角形。
程序如下：
subplot(2,2,1);
bar3(magic(4))
subplot(2,2,2);
y=2*sin(0:pi/10:2*pi);
stem3(y);
subplot(2,2,3);
pie3([2347,1827,2043,3025]);
subplot(2,2,4);
fill3(rand(3,5),rand(3,5),rand(3,5), 'y' )
例 绘制多峰函数的瀑布图和等高线图。
程序如下：
subplot(1,2,1);
[X,Y,Z]=peaks(30);
waterfall(X,Y,Z)
xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis');
subplot(1,2,2);
contour3(X,Y,Z,12,'k'); %其中12代表高度的等级数
xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis');

图形修饰处理
视点处理
MATLAB提供了设置视点的函数view，其调用格式为：
view(az,el)
其中az为方位角，el为仰角，它们均以度为单位。系统缺省的视点定义为方位角-37.5°,仰角30°。
例 从不同视点绘制多峰函数曲面。
程序如下：
subplot(2,2,1);mesh(peaks);

view(-37.5,30); %指定子图1的视点
title('azimuth=-37.5,elevation=30')
subplot(2,2,2);mesh(peaks);
view(0,90);
%指定子图2的视点
title('azimuth=0,elevation=90')
subplot(2,2,3);mesh(peaks);

view(90,0);
%指定子图3的视点
title('azimuth=90,elevation=0')
subplot(2,2,4);mesh(peaks);

view(-7,-10);
%指定子图4的视点
title('azimuth=-7,elevation=-10')
色彩处理
1．颜色的向量表示
MATLAB除用字符表示颜色外，还可以用含有3个元素的向量表示颜色。向量元素在[0,1]范围取值，3个元素分别表示红、绿、蓝3种颜色的相对亮度，称为RGB三元组。
2．色图
色图(Color map)是MATLAB系统引入的概念。在MATLAB中，每个图形窗口只能有一个色图。色图是m×3 的数值矩阵，它的每一行是RGB三元组。色图矩阵可以人为地生成，也可以调用MATLAB提供的函数来定义色图矩阵。
3．三维表面图形的着色
三维表面图实际上就是在网格图的每一个网格片上涂上颜色。surf函数用缺省的着色方式对网格片着色。除此之外，还可以用shading命令来改变着色方式。
shading faceted命令将每个网格片用其高度对应的颜色进行着色，但网格线仍保留着，其shading
flat命令将每个网格片用同一个颜色进行着色，且网格线也用相应的颜色，从而使得图形表面显得更加光滑。
shading interp命令在网格片内采用颜色插值处理，得出的表面图显得最光滑。
颜色是黑色。这是系统的缺省着色方式
例 3种图形着色方式的效果展示。
程序如下：
[x,y,z]=sphere(20);
colormap(copper);
subplot(1,3,1);
surf(x,y,z);
axis equal
subplot(1,3,2);
surf(x,y,z);shading flat;
axis equal
subplot(1,3,3);
surf(x,y,z);shading interp;
axis equal
光照处理
MATLAB提供了灯光设置的函数，其调用格式为：
light('Color',选项1,'Style',选项2,'Position',选项3)
光照处理后的球面。
程序如下：
[x,y,z]=sphere(20);
subplot(1,2,1);
surf(x,y,z);axis equal;
light('Posi',[0,1,1]);
shading interp;
hold on;
plot3(0,1,1,'p');text(0,1,1,' light');
subplot(1,2,2);
surf(x,y,z);axis equal;
light('Posi',[1,0,1]);
shading interp;
hold on;
plot3(1,0,1,'p');text(1,0,1,' light');
图形的裁剪处理
例4-22 绘制三维曲面图，并进行插值着色处理，裁掉图中x和y都小于0部分。
程序如下：
[x,y]=meshgrid(-5:0.1:5);
z=cos(x).*cos(y).*exp(-sqrt(x.^2+y.^2)/4);
surf(x,y,z);shading interp;
pause
%程序暂停
i=find(x<=0&y<=0);
z1=z;z1(i)=NaN;
surf(x,y,z1);shading interp;
为了展示裁剪效果，第一个曲面绘制完成后暂停，然后显示裁剪后的曲面。

图像处理与动画制作
图像处理
1．imread和imwrite函数
imread和imwrite函数分别用于将图像文件读入MATLAB工作空间，以及将图像数据和色图数据一起写入一定格式的图像文件。MATLAB支持多种图像文件格式，如.bmp、.jpg、.jpeg、.tif等。
2．image和imagesc函数
这两个函数用于图像显示。为了保证图像的显示效果，一般还应使用colormap函数设置图像色图。
例5-23 有一图像文件flower.jpg，在图形窗口显示该图像。
程序如下：
[x,cmap]=imread('flower.jpg'); %读取图像的数据阵和色图阵
image(x);colormap(cmap);
axis image off %保持宽高比并取消坐标轴
动画制作
MATLAB提供getframe、moviein和movie函数进行动画制作。
1．getframe函数
getframe函数可截取一幅画面信息(称为动画中的一帧)，一幅画面信息形成一个很大的列向量。显然，保存n幅图面就需一个大矩阵。
2．moviein函数
moviein(n)函数用来建立一个足够大的n列矩阵。该矩阵用来保存n幅画面的数据，以备播放。之所以要事先建立一个大矩阵，是为了提高程序运行速度。
3．movie函数
movie(m,n)函数播放由矩阵m所定义的画面n次，缺省时播放一次。
例 绘制了peaks函数曲面并且将它绕z轴旋转。
程序如下
[X,Y,Z]=peaks(30);
surf(X,Y,Z)
axis([-3,3,-3,3,-10,10])
axis off;
shading interp;
colormap(hot);
m=moviein(20);
%建立一个20列大矩阵
for i=1:20
view(-37.5+24*(i-1),30) %改变视点
m(:,i)=getframe;
%将图形保存到m矩阵
end
movie(m,2); %播放画面2次 参考技术C 不知道学了matlab没有？如果没有，在这里是说不清楚的。如果已经学了，建议找本“matlab与信号处理”的书，一般里面都有你需要的程序的。因为这些程序非常经典。

备战数学建模3-MATLAB绘制各种二维图形

目录

MATLAB二维曲线及二维图形

 1-plot(x,y)函数的基本用法

          2-fplot(f,lim,选项)函数的基本用法

 3-subplot(m,n,p)函数的基本用法

4- polar(theata,rho,选项)函数的基本用法

 5-bar(y,style)函数的基本用法

6-hist(y,x)函数和rose(theta,x)函数的基本用法

7-pie(x,explode)函数和area()函数的用法

 8-scatter()函数、stairs()函数、stem()函数的应用

 9-compass()函数、feather()函数、quiver()函数的应用

---

MATLAB二维曲线及二维图形

1-plot(x,y)函数的基本用法

plot(x,y)函数的基本用法：其中分别用于存储x坐标和y的坐标。

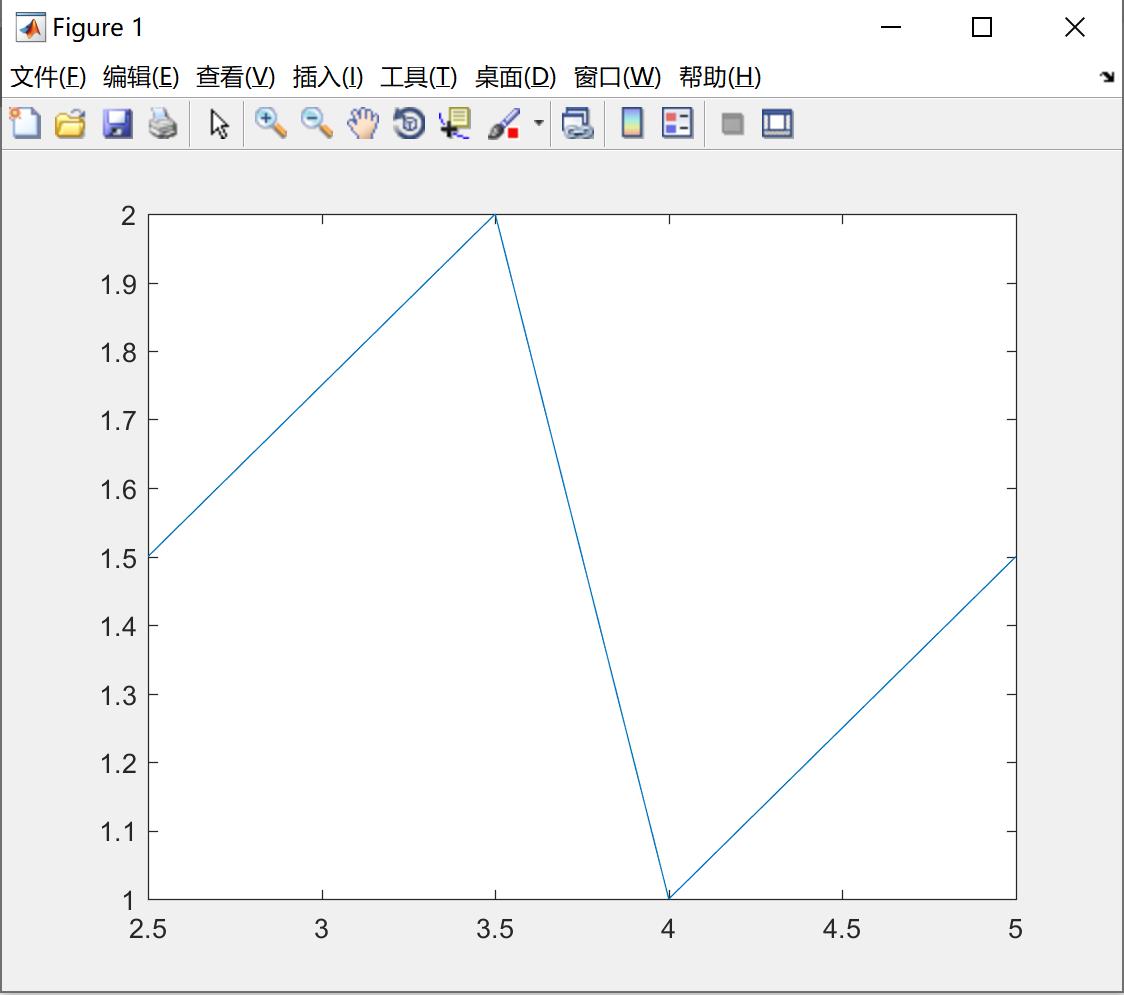
我们看一下例子1，用plot函数绘制一条折线。代码如下：

x = [2.5, 3.5, 4, 5] ;
y = [1.5, 2.0, 1, 1.5] ;
plot(x,y);

 绘制的折线图如下所示：

如果plot()函数中只有参数x，则x作为纵坐标，x对应的位置作为横坐标。

如下代码的横坐标是1，2，3，4，纵坐标为向量x中的值。

x = [2,3,4,5] ;
plot(x) ;

当plot函数的参数x是复数向量的时候，分别以该向量元素的实部和虚部作为横纵坐标，绘制一条折线。

x = [2.5, 3.5, 4, 5] ;
y = [1.5, 2, 1, 1.5] ;
cx = complex(x,y) ;
plot(cx) ;

绘制的图形如下所示：

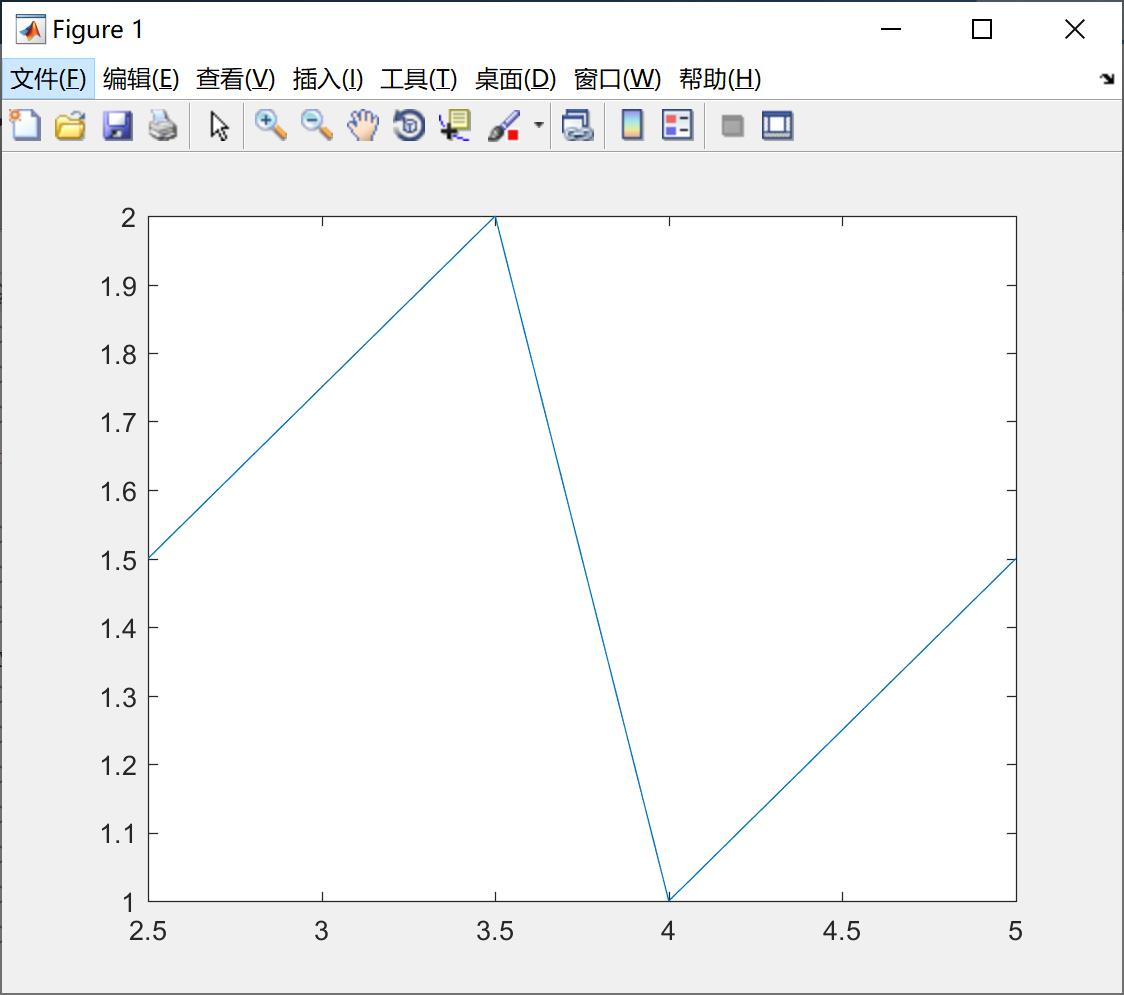
plot(x,y)函数参数的变化形式：

当x是向量，y是矩阵时，如果矩阵y的列数等于x的长度，则以向量x的为横坐标，以y的每个行向量为纵坐标绘制曲线，曲线的条数等于y的行数。

如果矩阵y的行数等于x的长度，则以向量x为横坐标，以y的每个列向量为纵坐标绘制曲线，曲线的条数等于y的列数。

看一下例子2，矩阵y的行向量与行向量x的长度相同，代码如下：

x = linspace(0,2*pi,100) ;
y = [sin(x); sin(2*x); sin(0.5*x)] ;
plot(x,y) ;

 绘制的图形如下所示：

上述代码也可以写成入戏的形式，代码如下：

t = 0 : 0.01 : 2*pi ;
t1 = t' ;
x = [t1, t1, t1];
y = [sin(t1),sin(2*t1),sin(0.5*t1)] ;
plot(x,y) ;

含有多个输入的plot()函数，使用向量对的方式，每个向量对构成 一组数据的横纵坐标，绘制出图形。

看一下例子3，我们使用10个，20个，100个数据点绘制正弦曲线，会发现数据点越多曲线越光滑。代码如下所示：

t1 = linspace(0,2*pi,10) ;
t2 = linspace(0, 2*pi, 20) ;
t3 = linspace(0, 2*pi, 100) ;
plot(t1,sin(t1),t2,sin(t2)+1,t3,sin(t3)+2) ;

绘制的图形入下所示：

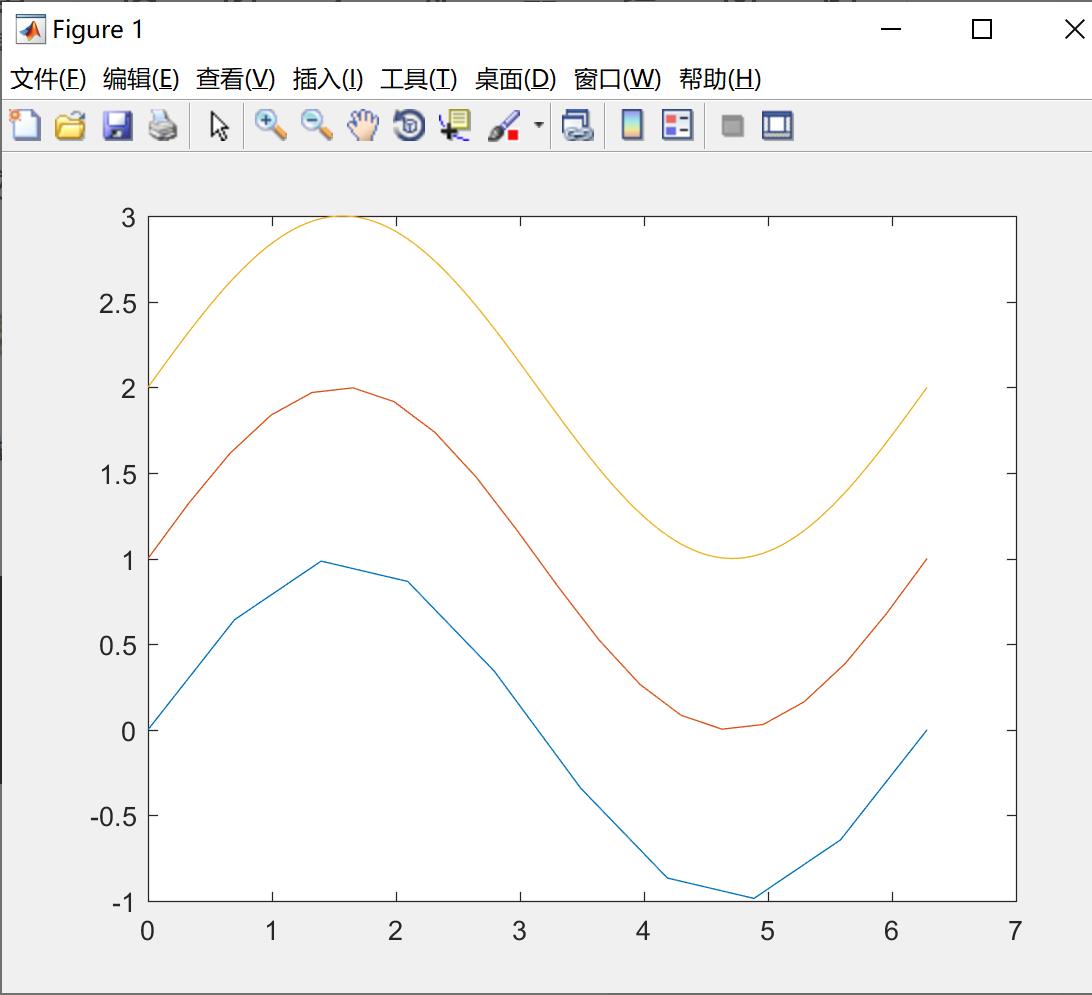
含选项的plot函数，plot(x,y,选项)函数，选项用于指定线型，颜色，数据点标记。

线型有如下几种常用的：

“-” ：实线    “：”：虚线   “-.”：点画线  “--”双画线

颜色一般用英文的首字母字母开头，例如：

“r” ：红色  “g”：绿色  “b”：蓝色  “w”：白色  “k”：黑色

数据点标记常用的如下所示：

“*” ：星号  “o”:圆圈  “s”：方形  “p”：五角星  “^”:朝上三角形 ‘d’：菱形

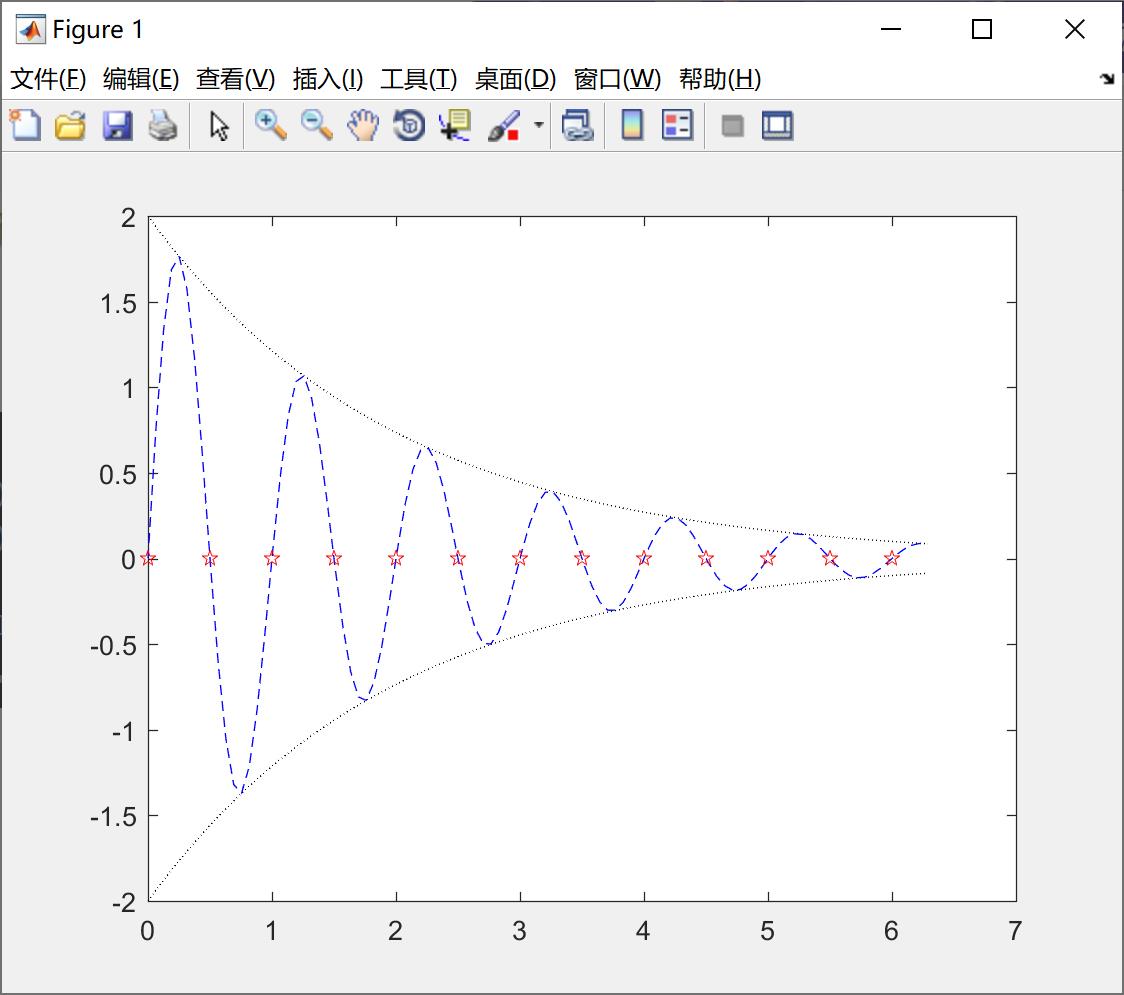
我们看一下上面的例子4，代码如下所示：

x = (0:pi/50:2*pi)' ;
y1 = 2 * exp(-0.5*x)*[1,-1];
y2 = 2 * exp(-0.5*x).*sin(2*pi*x);
x1 = 0:0.5:6 ;
y3 = 2 * exp(-0.5*x1).*sin(2*pi*x1) ;
plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp') ;

 绘制的图形如下所示：

 2-fplot(f,lim,选项)函数的基本用法

自适应设置间隔绘图的函数fplot(f,lim,选项),自适应间隔，一般波动变化较大的间隔设大一些，波动变化较小的，间隔设置小一点。其中f代表一个函数，通常采用函数句柄的形式，lims表示x轴的取值范围，用二元向量[xmin,xmax]表示，默认为[-5,5]，选项部分与plot()函数相同。

我们看一下上面例子6，具体的代码如下：

fplot(@(x) sin(1./x), [0,0.2], 'b') ;

 绘制的图形如下所示：

双输入函数参数的用法：fplot(funx,funy,tlims,选项)

 我们看一下上面的例子，具体的代码如下所示：

fplot(@(t) t.*sin(t), @(t) t.*cos(t), [0, 10*pi], 'r') ;

 绘制的图形如下所示：

 绘制图形的辅助操作

图形标注包括：title(图形标题)，xlabel(x轴说明)，ylabel(y轴说明)，text(x,y,图形说明)，legend(图例1，图例2，...)

我们看一下上面的例子1，绘制图形并添加标题，代码入下：

x = -2*pi : 0.05 : 2*pi ;
y = sin(x) ;
plot(x,y) ;
title('y=sinx') ;

 绘制的图形如下所示：

 在图形标题中使用Latex格式控制符。

含有属性的title(图形标题，属性名，属性值)：其中Color属性设置标题颜色，FrontSize属性设置标题大小。

xlabel(x轴说明)

ylabel(y轴说明)

下面我们绘制sinx的函数，并添加标题和标签，代码如下：

x = -2*pi : 0.05 : 2*pi ;
>> y = sin(x) ;
>> plot(x,y) ;
>> title('y=sinx') ;
>> xlabel('-2\\pi\\leqx\\leq2\\pi') ;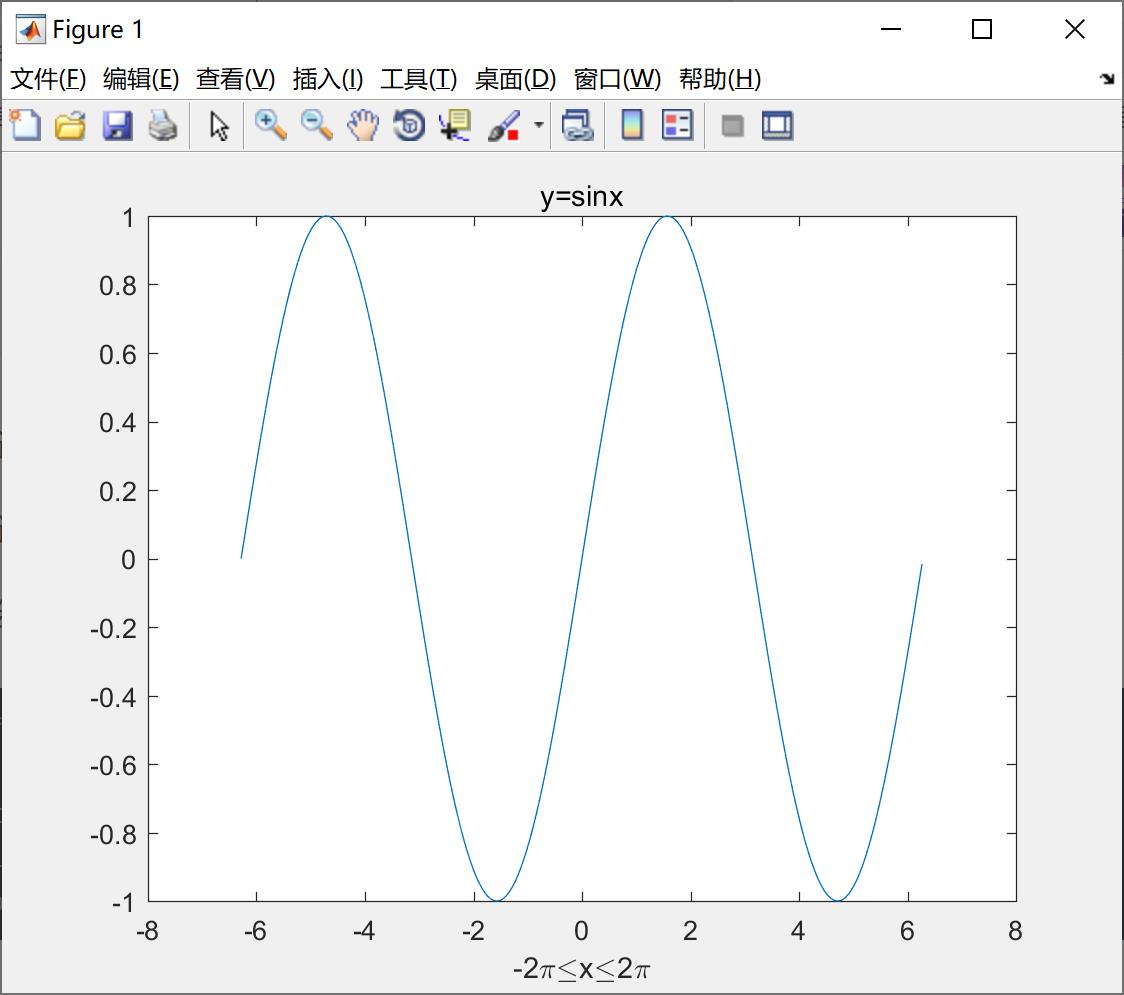

 legend(图例1，图例2，...)

 我们看一下例子2，关于legend()函数的使用，代码入下：

x = linspace(0, 2*pi, 100) ;
plot(x,[sin(x); sin(2*x); sin(3*x)]) ;
legend('sin(x)', 'sin(2x)', 'sin(3x)') ;

坐标控制，一般使用axis([xmin,xmax,ymin,ymax,zmin,zmax]) 函数来实现。这是三维的了，两维的只需要x和y就够了。

我们看一个画正方形的例子，代码如下所示：

x = [0,1,1,0,0] ;
y = [0,0,1,1,0] ;
plot(x,y) ;
axis([-0.1,1.1,-0.1,1.1]) ;
axis equal ; %设置横纵坐标轴采用等行刻度

绘出的图形如下所示：

给坐标系加网格线命令：grid on ,给坐标系加边框，box on 命令。

我们看一下例子3，通过例子3对图形标注命令进行复习，代码如下所示：

x = linspace(0,2*pi,100) ;
y = [sin(x); sin(2*x); sin(0.5*x)] ;
plot(x,y) ;
axis([0,7,-1.2,1.2]) ;
title('不同频率的正弦函数曲线图') ;
xlabel('Xvariable') ;
ylabel('Yvariable') ;
text(2.5, sin(2.5), 'sin(x)') ;
text(1.5, sin(2*1.5), 'sin(2x)') ;
text(5.5, sin(0.5*5.5), 'sin(0.5x)') ;
legend('sin(x)','sin(2x)','sin(0.5x)') ;

 绘制的图形如下所示，图中有标题，标签，图例等标注。

hold on 命令保持原图形窗口，hold off命令刷新图形窗口，hold命令在两种命令之间切换。

我们看一下上面的例子4，使用图形保持功能在一幅图中绘制两个同心圆，代码如下所示：

t = linspace(0, 2*pi, 100) ;
x = sin(t) ;
y = cos(t) ;
plot(x,y,'b') ;
hold on ;
plot(2*x,2*y,'r--') ;
grid on ;
axis([-2.2,2.2,-2.2,2.2]) ;
axis equal ;

绘制的图形如下所示：

 3-subplot(m,n,p)函数的基本用法

图形窗口的分割：同一窗口中不同坐标系下的图形称为子图，使用subplot(m,n,p)函数，代表划分成m*n个窗口，并在第p个窗口绘图。

把正弦函数和余弦函数花在一个图中，代码如下所示：

x1 = linspace(0,2*pi,100) ;
subplot(1,2,1) ;
plot(x1, sin(x1), 'r') ;
grid on ;
axis equal ;
axis([0, 2*pi, -1, 1]) ;
title('正弦曲线图形') ;
xlabel('x') ;
ylabel('sinx') ;
subplot(1,2,2);
plot(x1, cos(x1), 'b') ; 
grid on ;
axis equal ;
axis([0, 2*pi, -1, 1]) ;
title('余弦曲线图形') ;
xlabel('x') ;
ylabel('cosx') ;

绘制的图形如下所示：

其它形式的二维曲线：

对数坐标图：我们看一下例子就可以。

在一个窗口绘制四种坐标图，代码如下所示：

x = 0 : 0.1 : 10 ;
y = 1./x ;
subplot(2,2,1) ;
plot(x,y) ;
title('plot(x,y)') ;
subplot(2,2,2) ;
semilogx(x,y) ;
title('semilogx(x,y)') ;
subplot(2,2,3) ;
semilogy(x,y) ;
title('semilogy(x,y)') ;
subplot(2,2,4) ;
loglog(x,y) ;
title('loglog(x,y)') ;

绘制的图形入戏所示：

4- polar(theata,rho,选项)函数的基本用法

 polar(theata,rho,选项)绘制极坐标图，theta表示极角，rho代表极径，选项与plot相同。

我们看一下例子2，通过极角和极径绘制极坐标图形，代码如下所示：

t = 0 : pi/100 : 2*pi ;
r = 1 - sin(t) ;
subplot(1,2,1) ;
polar(t,r) ;
subplot(1,2,2) ;
t1 = t - pi/2 ;
r1 = 1 - sin(t1) ;
polar(t,r1) ;

 绘制的图形如下所示：

 5-bar(y,style)函数的基本用法

下面开始学习绘制统计图。

条形图的绘制：可以使用bar(y,style)函数绘制条形图，其中y是参数数据，style是分组排列模式，有簇状模式grouped和堆积模式stacked两种形式。

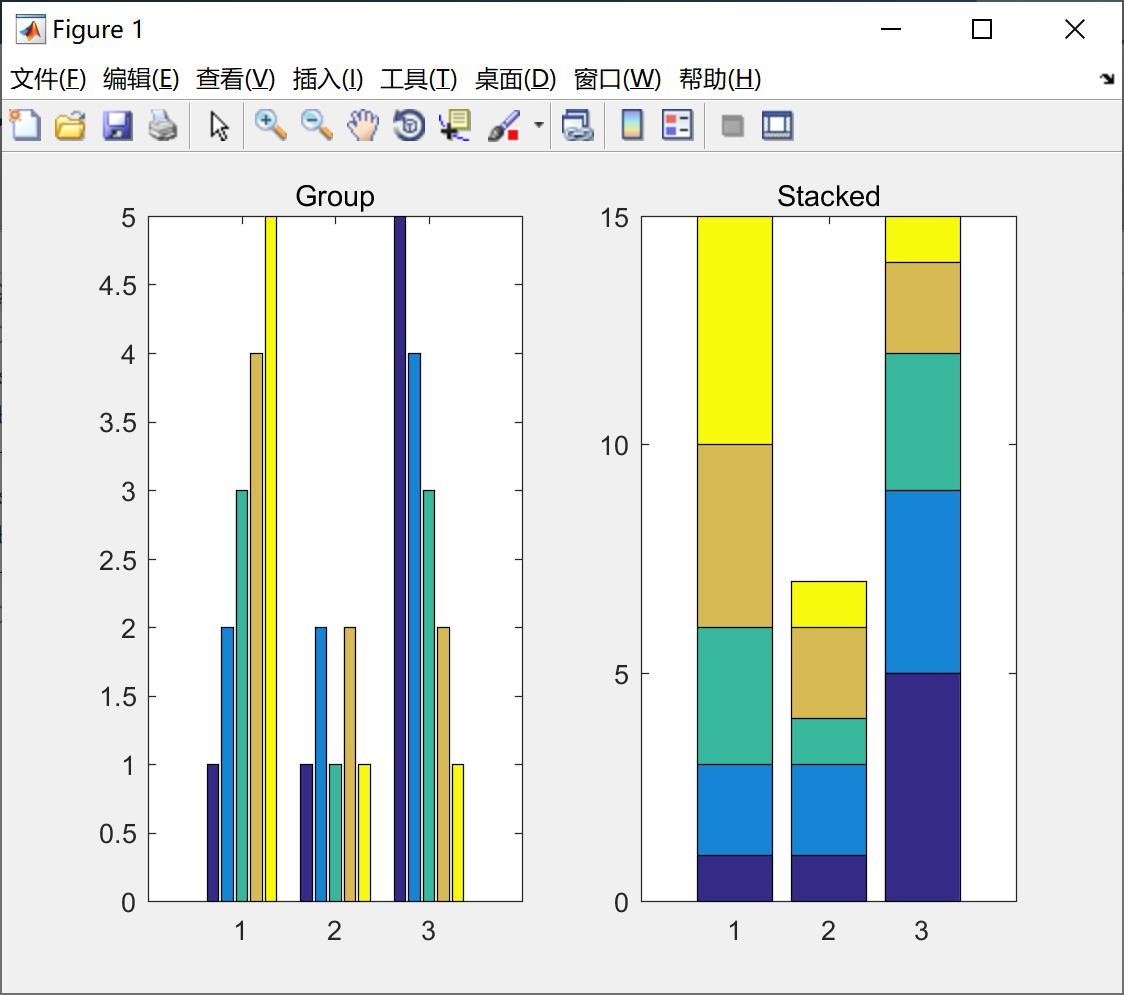
我们可以看一下例子3的绘制分组条形图，代码如下所示：

y = [1,2,3,4,5; 1,2,1,2,1; 5,4,3,2,1] ;
subplot(1,2,1) ;
bar(y) ;
title('Group') ;
subplot(1,2,2) ;
bar(y, 'stacked') ;
title('Stacked') ;

绘制的图形如下所示： 

 

我们再看一下上面的例子4，绘制条形图，代码如下所示：

x = [2015, 2016, 2017] ;
y = [68,80,115,98,102; 75,88,102,99,110; 81,86,125,105,115] ;
bar(x,y) ;
title('2015~2017年公司家电销售数据') ;

绘制的图形如下所示:

6-hist(y,x)函数和rose(theta,x)函数的基本用法

我们学习使用hist函数绘制直角坐标下的直方图和rose函数绘制极坐标下的直方图

hist(y,x)函数，y表示要统计的数据，x是指定的区间划分方式。

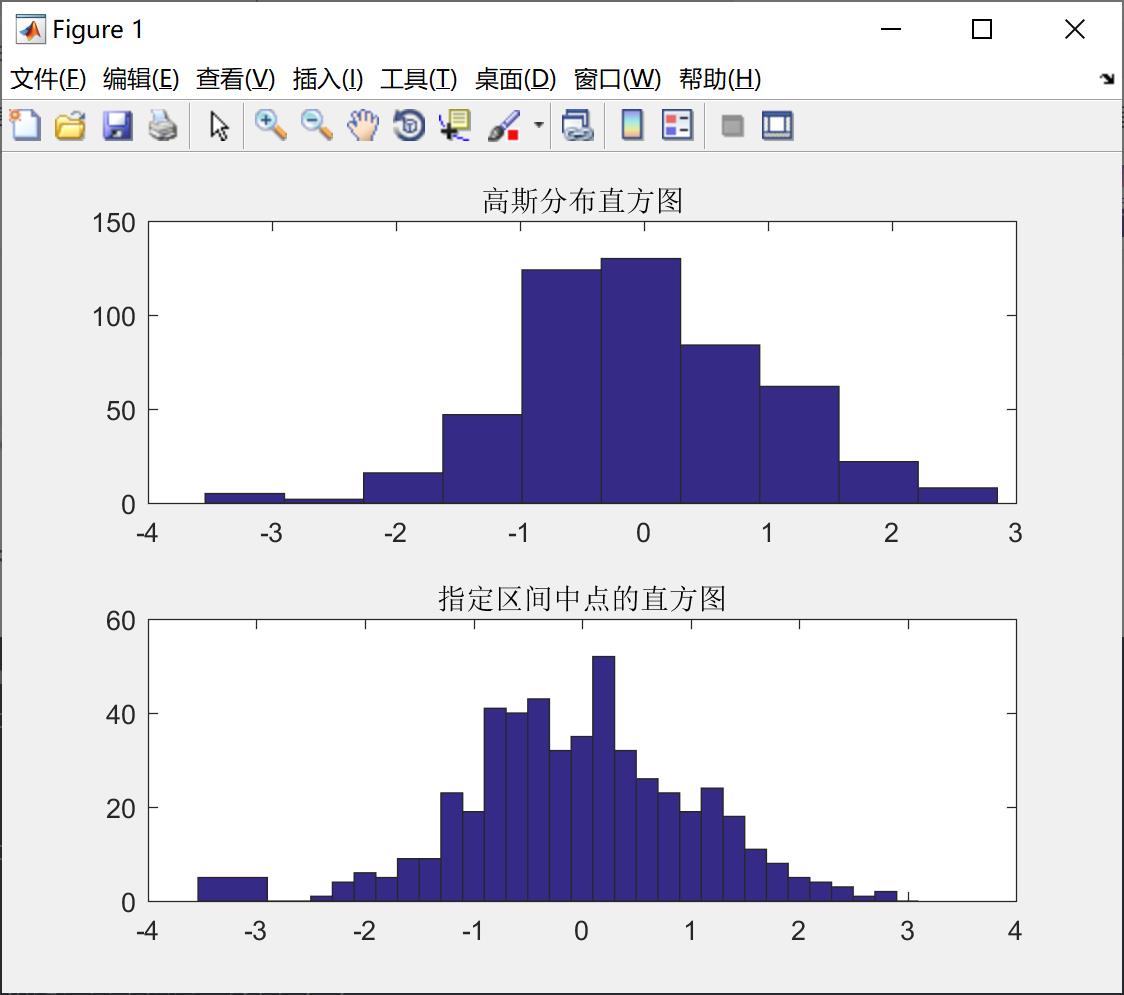
我们看一下例子5，绘制服从高斯分布的直方图，代码如下所示：

y =  randn(500, 1) ;
subplot(2,1,1) ;
hist(y) ;
title('高斯分布直方图') ;
subplot(2,1,2) ;
x = -3:0.2:3 ;
hist(y,x) ;
title('指定区间中点的直方图') ;

 绘制的直方图如下所示：

 使用rose(theta,x)函数用于绘制极坐标系下的直方图。参数theta用于确定每一区间和原点的角度，选项x用于指定区间的划分方式。

 我们看一下例子6，绘制高斯分布在极坐标下的直方图，代码如下：

y = randn(500,1) ;
theta = y * pi ;
rose(theta) ;
title('在极坐标下的直方图') ;

7-pie(x,explode)函数和area()函数的用法

pie(x,explode)用于绘制扇形图，其中参数x存储待统计的数据，选项explode控制图块的显示模式。

我们看一下例子7，代码如下所示：

score = [5,17,23,9,4] ;
ex = [0,0,0,0,1] ;  %存储图形显示控制符，将最后一个移出来
pie(score, ex) ;
legend('优秀','良好','中等','及格','不及格','location','eastoutside') ;

绘制的扇形图如下所示：

 8-scatter()函数、stairs()函数、stem()函数的应用

三个类似，这边只介绍scatter(x,y,选项，‘field’)函数，其中x,y用于定位数据点，选项用于指定线形，颜色，数据点标记。

scattter()函数用于画散点图，我门看一下例子8，代码如下所示：

t = 0 : pi/50 : 2*pi ;
x = 16*sin(t).^3 ;
y = 13*cos(t) - 5*cos(2*t)- 2*cos(3*t) - cos(4*t) ;
scatter(x,y,'rd','filled') ;

绘制的心形图形如下所示：

 9-compass()函数、feather()函数、quiver()函数的应用

compass()函数用于绘制罗盘图，feather()函数用于绘制羽毛图，quiver()函数用于绘制箭头图，用法和plot()函数类似。

例如:quiver(x,y,u,v)函数，其中(x,y)为矢量起点，(u,v)为矢量终点。

我们看一下上面的例子9，代码如下所示：

A = [4,5] ;
B = [-10, 0] ;
C = A + B ;
hold on ;
quiver(0,0,A(1),A(2)) ;
quiver(0,0,B(1),B(2)) ;
quiver(0,0,C(1),C(2)) ;
text(A(1),A(2),'A') ;
text(B(1),B(2),'B') ;
text(C(1),C(2),'C') ;
axis([-12,6,-1,6]) ;
grid on ;

 绘制的矢量图形如下所示：

超强干货来袭 云风专访：近40年码龄，通宵达旦的技术人生