因果推断笔记——DR ：Doubly Robust学习笔记（二十）

Posted 2022-02-03 悟乙己

文章目录

• 0 观测数据的估计方法
• • 0.1 Matching
  • 0.2 Propensity Score Based Methods
  • • 0.2.1 PSM
    • 0.2.2 IPW
    • 0.2.3 Doubly Robust
    • 0.2.4 Covariate balancing propensity score (CBPS)
    • 0.2.5 数据驱动的变量分解算法（D²VD）
  • 0.3 Directly Confounder Balancing
  • • 0.3.1 Entrophy Balancing
    • 0.3.2 Approximate Residual Balancing
• 1 DR ：Doubly Robust
• • 1.1 DR的理论基础
  • • 1.1.1 ATE的估计
    • 1.1.2 CATE的估计
  • 1.2 DR 与DML的异同
• 2 econml的实现

这个系列文章：
因果推断笔记——python 倾向性匹配PSM实现示例（三）
因果推断笔记——DML ：Double Machine Learning案例学习（十六）

---

0 观测数据的估计方法

参考：

• 如何在观测数据下进行因果效应评估
• 因果推断综述解析|A Survey on Causal Inference(3)

在rubin的理论下，
在观测数据下，为了给实验组寻找合适的对照组，或者消除对照组的影响，有非常多种方式，其中包括：

• Matching（找对照组）
• Propensity Score Based Methods（PS中介变量过度）
  • PS Matching ，能解决在高维数据中难以找到相似样本的问题
  • Inverse of Propensity Weighting 方法（IPW）
  • Doubly Robust
• Directly Confounder Balancing（直接对样本权重进行学习）
  • Entrophy Balancing 方法之中，通过学习样本权重，使特征变量的分布在一阶矩上一致，同时还约束了权重的熵（Entropy）
  • Approximate Residual Balancing。第一步也是通过计算样本权重使得一阶矩一致，第二步与 Doubly Robust 的思想一致，加入了回归模型，并在第三步结合了前两步的结果估计平均因果效应。

0.1 Matching

大牛论文：
Matching methods for causal inference: A review and a look forward

0.2 Propensity Score Based Methods

关于PS：
Rubin 证明了在给定倾向指数的情况下，Unconfounderness 假设就可以满足。倾向指数其实概括了群体的特征变量，如果两个群体的倾向指数相同，那他们的干预变量就是与其他特征变量相独立的。

0.2.1 PSM

其中PS的方式也可以与Matching进行结合，也就是PSM；
做 Matching，这样能解决在高维数据中难以找到相似样本的问题

0.2.2 IPW

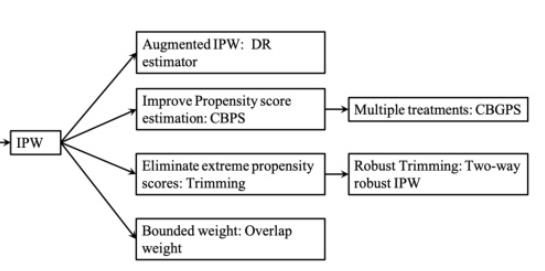
Inverse of Propensity Weighting 方法，对于干预变量为1的样本使用倾向指数的倒数进行加权，而对于为0的样本使用（1-倾向指数）的倒数进行加权，两类样本的加权平均值之差就是平均因果效应的大小。
这里有一个假设，就是估计出的倾向指数与真实的倾向指数是相等的。

因此这个方法有两个弱点，

• 一是需要对倾向指数的估计足够精确
• 二是如果倾向指数过于趋近0或1，就会导致某些权重的值过高，使估计出的平均因果效应的方差过大。

其他关联可见：倾向得分方法的双重稳健且有效的改进

经过IPW加权之后，我们大致认为各组样本之间不存在选择性偏差，这时，我们用对照组的观测结果的加权值来估计整体的对照策略的潜在结果期望，用试验组的观测结果的加权值来估计整体的试验策略的潜在结果期望。

0.2.3 Doubly Robust

IPW需要样本权重主要围绕倾向的分为核心，倾向得分一旦预测不准，会导致上面的估计方法出现很大的偏差。

为了解决样本权重过度依赖倾向得分准确性的问题， 大佬又提出了Doubly Robust estimator (DR)方法或者成为增强IPW(AIPW)。
DR方法具体做法类似于鸡蛋不放在一个篮子里的投资方法，它结合倾向得分和结果回归模型来得到样本权重，其具体做法如下：

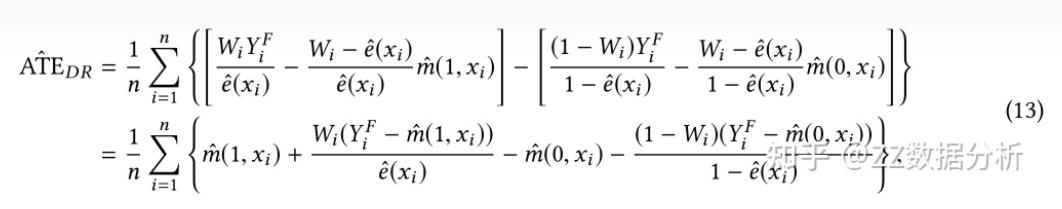
这个方法需要根据已有数据，再学习一个预测的模型，反事实评估某个个体在干预变量变化后，结果变量的期望值。
只要倾向指数的估计模型和反事实预测模型中有一个是对的，计算出的平均因果效应就是无偏的；
但如果两个模型估计都是错误的，那产生的误差可能会非常大。

0.2.4 Covariate balancing propensity score (CBPS)

因果推断综述解析|A Survey on Causal Inference(3)

IPW方法的倾向得分其实是策略的倾向选择概率，但是选择性偏差带来的是样本之间其他相关变量分布的不平衡。所以使用逆倾向得分属于只考虑了策略的倾向选择概率，却用来平衡样本之间其他相关变量的分布。Covariate balancing propensity score (CBPS)，协变量平衡倾向得分方法被设计出来来同时衡量这两方面，来使倾向得分更准确。CBPS得到倾向得分的方式是求解下面的方程：

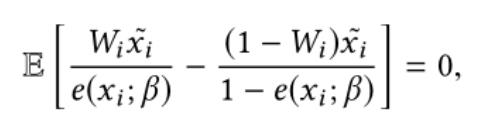
0.2.5 数据驱动的变量分解算法（D²VD）

以上的这三种基于倾向指数的方法比较粗暴，把干预变量和结果变量之外的所有变量都当作混淆变量。而在高维数据中，我们需要精准地找出那些真正需要控制的混淆变量。我们提出了一种数据驱动的变量分解算法（D²VD），将干预变量和结果变量之外的其他变量分为了三类：

1. 混淆变量（Confounders）：既会影响到干预变量，还会影响到结果变量

2. 调整变量（Adjustment Variables）：与干预变量独立，但会影响到结果变量

3. 无关变量：不会直接影响到干预变量与结果变量

进行分类之后，就可以只用混淆变量集去估计倾向指数。而调整变量集会被视为对结果变量的噪声，进行消减。最后使用经过调整的结果，去估计平均因果效应。我们从理论上证明了，使用这种方法可以得到无偏的平均因果效应估计，而且估计结果的方差不会大于 Inverse of Propensity Weighting 方法。

0.3 Directly Confounder Balancing

直接对样本权重进行学习。
这类方法的动机就是去控制在干预变量下其他特征变量的分布。
上述的样本加权方法可以在将观测到样本其他变量均视为混杂因素的意义上实现平衡。
然而，在实际情况中，并非所有观察到的变量都是混杂因素。有些变量被称为调整变量，只是对结果有影响，还有一些可能是无关的变量。

0.3.1 Entrophy Balancing

方法之中，通过学习样本权重，使特征变量的分布在一阶矩上一致，同时还约束了权重的熵（Entropy）。但这个方法的问题也是将所有变量都同等对待了，把过多变量考虑为混杂变量。

0.3.2 Approximate Residual Balancing

第一步也是通过计算样本权重使得一阶矩一致，第二步与 Doubly Robust 的思想一致，加入了回归模型，并在第三步结合了前两步的结果估计平均因果效应。只要样本权重的估计和反事实预测模型中有一个是对的，计算出的平均因果效应就是无偏的。但这里也是将所有变量都同等对待了。

---

1 DR ：Doubly Robust

DR是在Propensity Score的分析体系下的，所以，

1.1 DR的理论基础

【因果推断/uplift建模】Doubly Robust Learning(DRL)

Doubly Robust Methods明显优点是两个预估量如果有一个是consistent，则ATE是估计是consistent；
还有一个优点是理论上比COM/IPW收敛更快，也就是说理论上数据利用效率更高，但是理论研究一般是基于infinite data进行的，真实环境中收敛速率也不一定。

1.1.1 ATE的估计

$\widehat{ATE}=\frac{1}{N}\sum (\frac{T_i(Y_i-\widehat{{\mu }_1}(X_i))}{\hat{P}(X_i)}+\widehat{{\mu }_1}(X_i))-\frac{1}{N}\sum (\frac{(1-T_i)(Y_i-\widehat{{\mu }_0}(X_i))}{1-\hat{P}(X_i)}+\widehat{{\mu }_0}(X_i))$

其中, $\hat{P}(x)$ 代表倾向性得分, $\widehat{{\mu }_1}(x)$ 是对 $E[Y|X,T=1]$ 的估计, $\widehat{{\mu }_0}(x)$ 是对 $E[Y|X,T=0]$ 的估计. 从公式上可以看到, 第一部分计算$E[Y_1]$, 第二部分计算$E[Y_0]$.

DRL的优点之一就是它只要求在倾向性得分估计模型和outcome估计模型中，其中一种是准确的即可,即 $\hat{P}(x)$ 或 $\hat{\mu }(x)$其中一种估计准确即可。 以 $E[Y_1]$ 为例：

$\hat{E}[Y_1]=\frac{1}{N}\sum (\frac{T_i(Y_i-\widehat{{\mu }_1}(X_i))}{\hat{P}(X_i)}+\widehat{{\mu }_1}(X_i))$

假设 $\widehat{{\mu }_1}(x)$ 是正确的. 即使倾向性得分模型是错的， 仍然有 $E[T_i(Y_i-\widehat{{\mu }_1}(X_i))]$

因果推断笔记——DR ：Doubly Robust学习笔记（二十）

因果推断推荐系统工具箱 - MRDR（一）

因果推断笔记——自整理因果推断理论解读

因果推断笔记——自整理因果推断理论解读

因果推断笔记——CV机器人领域因果推断案例集锦

因果推断笔记——CV机器人领域因果推断案例集锦