理想滤波器为啥不能实现?

Posted 2023-05-05

急，请高手帮忙！

因为非因果性，不符合Paley－Wiener准则在物理上是不可能的，但这对理论分析是很有帮助的。理想低通滤波器是一种假设的低通滤波器，它能完全切断高于截止频率的信号，并传输低于截止频率的信号而不失真。

一个非因果系统在当前时刻的输出不仅取决于当前的输入，也取决于未来的输入系统。

扩展资料：

在信号处理领域，理想低通滤波器是一种理想的电子滤波器，它去除给定带宽以上的所有信号成分，只保留低频信号。它在频域是一个矩形函数，在时域是一个Sinc函数。

由于理想低通滤波器（称为矩形滤波器）的无限延迟，实际滤波器只能是它们的近似，但它们仍然被广泛应用于概念证明或验证，如采样定理和惠特克－香农插值公式。

参考资料来源：百度百科-sinc滤波器

参考资料来源：百度百科-理想低通滤波器

参考资料来源：百度百科-因果系统

参考技术A 因为电感电容都是非线性的，高频的分布参数影响特性从而无法实现理想化。

电源滤波器是由电容、电感和电阻组成的滤波电路。滤波器可以对电源线中特定频率的频点或该频点以外的频率进行有效滤除，得到一个特定频率的电源信号，或消除一个特定频率后的电源信号。 参考技术B 根据佩利和维那准则，只要系统的幅频特性在某一宽度不为零的频带内恒为0,相应的系统就是不可以实现的。 参考技术C 理想低通滤波器在频域是一个矩形的，而转换到时域以后，就变成了一个非因果系统了，这个在电路(物理）上是无法实现的。本回答被提问者采纳 参考技术D 因为电感电容都是非线性的，高频的分布参数影响他们的特性从而无法实现理想化！

基于窗函数的FIR滤波器的matlab设计与实现

目录

一、理论基础

二、理论基础

三、仿真测试结果

---

一、理论基础

      数字滤波器的设计是现代数字信号处理的重要内容。常用的数字滤波器有FIR和IIR两种类型，两者比较而言。主要有如下几点区别：

      从系统的幅频特性来看，IIR滤波器由于综合利用了系统的零极点，容易达到比较理想的设计效果； 而FIR滤波器由于只有零点，效果较IIR滤波器差。要达到与IIR滤波器相似的效果，往往要提高系统的阶数。

      其次，从相位特性来看，用FIR滤波器可以得到线性相位数字滤波器，满足信号不失真传输的要求。 对于IIR滤波器而言，往往幅频特性越好，相位非线性就越严重。

       再次，从系统稳定性来看，FIR滤波器由于没有极点，所以一定是稳定的；而IIR滤波器的稳定与否取决于其极点的位置。

      最后，从设计方法来看，IIR滤波器的设计参照连续时间系统的传输函数进行，可以充分利用模拟滤波器的设计结果，但是要求设计者有一定的模拟滤波器的设计知识，而且必须保证在模拟滤波器中能够找到合适的滤波器原型作为设计基础；而FIR滤波器设计结果完全是根据系统频率进行，不需要设计者有其他滤波器的知识，设计方法比较简单。

 

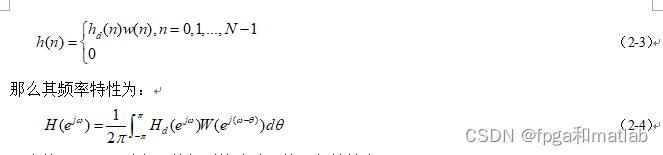
通常情况下，通过窗函数得到的滤波器的理想特性为：

    ·截止频率的间断点变成了连续的曲线，使其出现了一个过渡带，它的宽度等于窗函数的主瓣的宽度。所以，窗函数的主瓣越宽，过渡带就越宽。

    ·由于窗函数旁瓣的影响，使得滤波器的幅度频率特性出现了波动，波动的幅度取决于旁瓣的相对幅度.旁瓣范围的面积越大，通带波动和阻带的波动就越大，即阻带的衰减减小。而波动的大小，取决于旁瓣的大小。

     ·增加窗函数的长度，只能减少窗函数的幅度频率特性的主瓣宽度，而不能减少主瓣和旁瓣的相对值，该值取决于窗函数的形状。换句话说，增加截取函数的长度N只能相应的减小过渡带，而不能改变滤波器的波动程度。

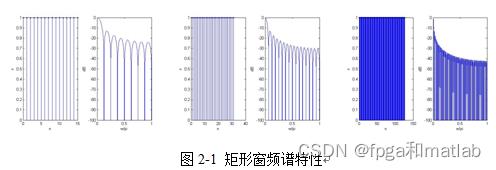
    常用的窗函数有矩形窗、海明窗、凯塞窗、汉宁(HanZning)窗等。

二、核心程序

clc,clear


Ts=1/1000  ;%设置采样频率
N=128;      %设置阶数
n=[0:(N-1)];
Wn=0.2;     %设置截止频率

t=0:Ts:3*pi;
y=sin(2*pi*t)+cos(8*pi*t)+cos(400*pi*t);

figure(1);plotspec(y,Ts);title('y');


%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法
%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法
k=input('请选择窗的类型:\\n 1、矩形窗\\n 2、汉宁窗\\n 3、汉明窗\\n 4、布拉克曼窗\\n');
switch k
    case 1
        x=win(0,N-1,0,N-1);                       %矩形窗
        figure,
        subplot(1,2,1);
        stem(n,x,'.');                            %得到数字信号波形表示方法函数STEM
        xlabel('n');                              %X坐标标签
        ylabel('x');                              %Y坐标标签
        string=['矩形窗时域图形','N=',num2str(N)];%波形标题
        text((0.6*N),0.8,string);                 %波形标题
        
        [H,m]=freqz(x,[1],1024,'whole');          %求其频率响应
.......................
        
    case 2
        x=win(0,N-1,0,N-1);
        x=(0.5-0.5*cos(2*pi*n/(N-1))).*x;
        figure,
        subplot(1,2,1);
        stem(n,x,'.');
        xlabel('n');
        ylabel('x');
        string=['汉宁窗时域图形','N=',num2str(N)];
        text((0.6*N),0.8,string);
        
........................
    case 3
        x=win(0,N-1,0,N-1);
        x=(0.54-0.46*cos(2*pi*n/(N-1))).*x;
        figure,
        subplot(1,2,1);
        stem(n,x,'.');
        xlabel('n');
        ylabel('x');
        string=['汉明窗时域图形','N=',num2str(N)];
        text((0.6*N),0.8,string);
        
............................       

    case 4
        x=win(0,N-1,0,N-1);
        x=(0.42-0.5*cos(2*pi*n/(N-1))+0.08*cos(4*pi*n/(N-1))).*x;
        figure,
        subplot(1,2,1);
        stem(n,x,'.');
        xlabel('n');
        ylabel('x');
        string=['布拉克曼窗时域图形','N=',num2str(N)];
        text((0.6*N),0.8,string);
        
.................................            

    
end

 

三、仿真测试结果

A25-002