设连通图G中的边集E=(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c),则从顶点a出发可以

Posted 2023-04-26

数据结构图的问题设连通图G中的边集E=(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c),则从顶点a出发可以得到一种深度优先遍历的顶点序列为（ ）.(A) abedfc (B) acfebd (C) aebdfc (D) aedfcb这是如何解出来的?求详解！！

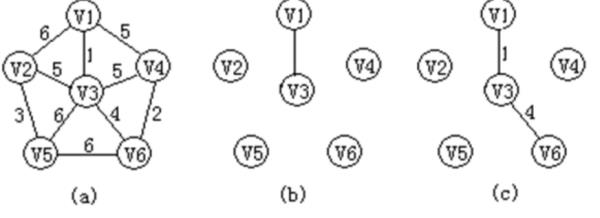
选择A。因为深度优先遍历的思想类似于树的先序遍历。其遍历过程可以描述为：从图中某个顶点v出发，访问该顶点，然后依次从v的未被访问的邻接点出发继续深度优先遍历图中的其余顶点，直至图中所有与v有路径相通的顶点都被访问完为止。

扩展资料：

连通分量：无向图 G的一个极大连通子图称为 G的一个连通分量（或连通分支）。连通图只有一个连通分量，即其自身；非连通的无向图有多个连通分量。

强连通图：有向图 G=(V,E) 中，若对于V中任意两个不同的顶点 x和 y，都存在从x到 y以及从 y到 x的路径，则称 G是强连通图。相应地有强连通分量的概念。强连通图只有一个强连通分量，即是其自身；非强连通的有向图有多个强连分量。

单向连通图：设G=<V,E>是有向图，如果u->v意味着图G至多包含一条从u到v的简单路径，则图G为单连通图。

参考技术A 选A，因为从题中就能看出要想经过f必须要经过d。（画出图就很明白了）
解析：深度优先遍历的思想类似于树的先序遍历。其遍历过程可以描述为：从图中某个顶点v出发，访问该顶点，然后依次从v的未被访问的邻接点出发继续深度优先遍历图中的其余顶点，直至图中所有与v有路径相通的顶点都被访问完为止。 参考技术B 除了B都对 参考技术C 深度遍历算法思路：首先访问图中某一起始顶点v,然后由v出发，访问与v邻接且未被访问的任一顶点w1，再访问与W1邻接且未被访问的任一顶点W2, ...重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止。
所以可以选ACD 题目错了 应该是选不是深度遍历的序列 谢谢采纳

二分图最大匹配

二分图的概念

二分图又称作二部图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

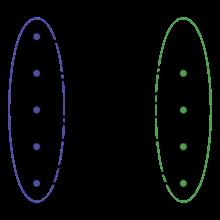
就长这个样。

最大匹配与增广路的概念

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。(源自百度-二分图匹配)

最大匹配即是选择其中边数最大的子集的图。

完全匹配，也叫做完备匹配，即某个匹配中，每个顶点都和某条边相关联。

好的，现在介绍完一个基本概念，我们就要着手解决如何求解最大匹配的问题了。

若要找出二分图中的最大匹配，最朴素的方法就是找出所有的匹配并一一比较，但这种方法的时间复杂度是边数的指数级的，不能满足数据范围较大的问题。因此，我们需要找出一个更优的方法求解。

在寻找这更优的方法前，我们需要先了解增广路的概念：增广路，也称增广轨或交错轨。若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径(举例来说，有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行)。（源自百度-增广路）

由增广路的定义我们可以推出下述三个结论：

1. P的路径长度必定为奇数，第一条边和最后一条边都不属于M。
2. 经过取反操作可以得到一个更大的匹配M’，边数为M的边数+1。

3. M为G的最大匹配当且仅当不存在相对于M的增广路径。

这里我们来介绍一种求二分图最大匹配的算法——匈牙利算法：

我们可以这样形象的描述匈牙利算法的原理：

我们相亲现场有五个男生和四个女生，假定一号男生喜欢（无特殊说明均视为两情相悦）一号和三号女生，二号喜欢一号，三号喜欢四号，四号喜欢三号和四号，五号喜欢三号。

那么我们模拟一下匈牙利的过程：

1、

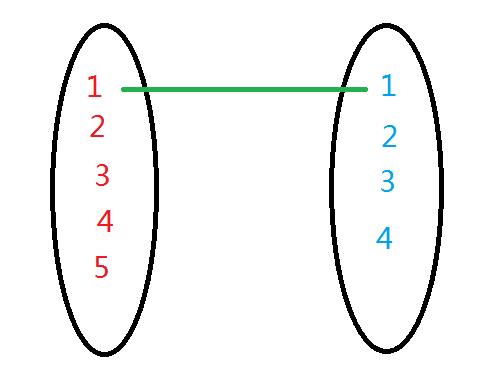
2、

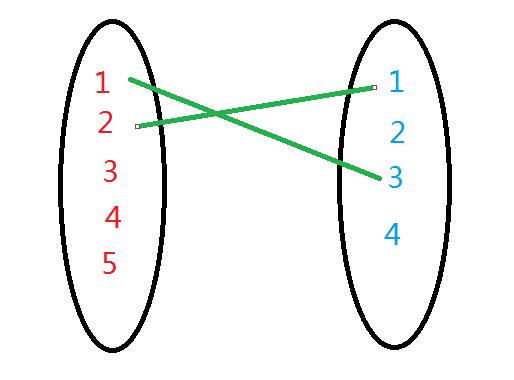
我们发现二号只能找一号，而一号还可以去找三号，所以我们让一去找三，而把一号女生给二号。

 3、

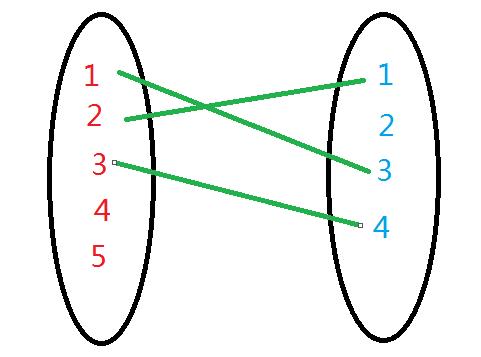
三去找四

4、

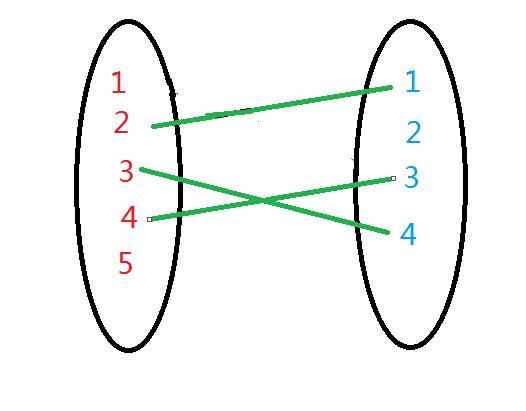
我们发现4号喜欢的女生都被选走了，怎么办？解决方法是令1单身而把3号女生给4号

5、

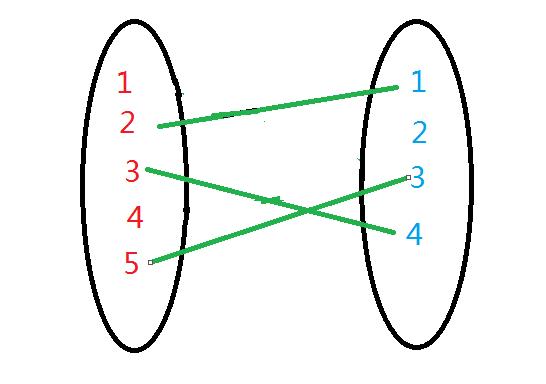
5号也喜欢3号，所以4号男生就凉了……

 

 总结：通过上面的例子我们发现匈牙利算法真的是瞎搞……这一秒你是人生赢家，下一秒可能就凉了。

于是我们用程序来模拟这个瞎搞的过程。

就是说如果你喜欢的女生没被选走或者选走她的人有其他选择那么她就是你的了。

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m,E,lin[100010],a[1000010],b[1000010],total,ans;
int M[1010][1010];
bool find(int now)
{
    for(int i=1;i<=m;i++)
    {
        if(!M[now][i]||b[i])continue;
        b[i]=1;
        if(!a[i]||find(a[i]))
        {
            a[i]=now;
            return 1;
        }
    }
    return 0;
}
int main()
{
    scanf("%d%d%d",&n,&m,&E);
    for(int i=1;i<=E;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        M[u][v]=1;
    }
    for(int i=1;i<=n;i++)
    {
        memset(b,0,sizeof(b));//记录是不是被找过 
        if(find(i))ans++;
    }
    printf("%d",ans);
}

例题：

1、

[ZJOI2009]假期的宿舍

 

 需要记录每个人是不是本校生。因为本校生有特权：自己可以睡自己的床（因为外校生没有床）。

 我们令人去匹配床，需要记住外校生没有床（外校生可视为回家），本校生可以睡自己的床。

在匹配过程中只要有一个没回家的人找不到床，匹配失败。

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
int t,n,lin[510],total,local[510],b[510],a[510],num,c[510];
int e[510][510];
bool find(int now)
{
    for(int i=1;i<=n;i++)
    {
        if(b[i]||!local[i]||!e[now][i])continue;
        b[i]=1;
        if(!a[i]||find(a[i]))
        {
            a[i]=now;
            return 1;
        }
    }
    return 0; 
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        total=0;
        memset(lin,0,sizeof(lin));
        memset(e,0,sizeof(e));
        memset(local,0,sizeof(local));
        memset(b,0,sizeof(b));
        memset(a,0,sizeof(a));
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        scanf("%d",&local[i]);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&c[i]);
            if(!local[i])
            c[i]=1;
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            scanf("%d",&e[i][j]);
            if(local[i])e[i][i]=1;
        }
        
        int judge=0;
        for(int i=1;i<=n;i++)
        {
            memset(b,0,sizeof(b));
            if((!local[i]||!c[i])&&!find(i))
            {
                judge=1;
                printf("T_T\\n");
                break;    
            }
        }
        if(!judge)
        printf("^_^\\n");
    }
}

 

2、

飞行员配对方案问题

 

 令外籍飞行员去匹配英国飞行员，求最大匹配数。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int m,n,lin[10010],total,ans,b[10010],a[10010];
struct cym{
    int from,to,next;
}e[10010];
void add(int x,int y)
{
    e[++total].from=x;
    e[total].to=y;
    e[total].next=lin[x];
    lin[x]=total;
}
bool find(int now)
{
    for(int i=lin[now];i;i=e[i].next)
    {
        if(b[e[i].to])continue;
        b[e[i].to]=1;
        if(!a[e[i].to]||find(a[e[i].to]))
        {
            a[e[i].to]=now;
            a[now]=e[i].to;
            return 1;
        }
    }
    return 0; 
}
int main()
{
    scanf("%d%d",&m,&n);
    int x,y;
    while(scanf("%d%d",&x,&y)!=EOF&&x!=-1)
    add(x,y);
    for(int i=1;i<=m;i++)
    {
        memset(b,0,sizeof(b));
        if(find(i))ans++;
    }
    if(!ans)
    printf("No Solution!");
    else
    {
        printf("%d\\n",ans);
        for(int i=1;i<=m;i++)
        if(a[i])printf("%d %d\\n",i,a[i]);
    }
}