怎样求曲线上某一点的斜率

Posted 2023-04-08

过曲线上的某一点做一条切线，求切线的斜率，切线的斜率就是曲线在该点的斜率。

分情况求解：

当直线L的斜率存在时，斜截式y=kx+b，当x=0时，y=b。

当直线L的斜率存在时，点斜式 

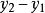
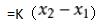
对于任意函数上任意一点，其斜率等于其切线与x轴正方向所成的角，即k=tanα。

斜率计算：ax+by+c=0中，

 

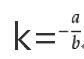
两条垂直相交直线的斜率相乘积为-1：

扩展资料：

1、斜率公式：

（1）当直线L的斜率存在时，斜截式y=kx+b 当k=0时 y=b

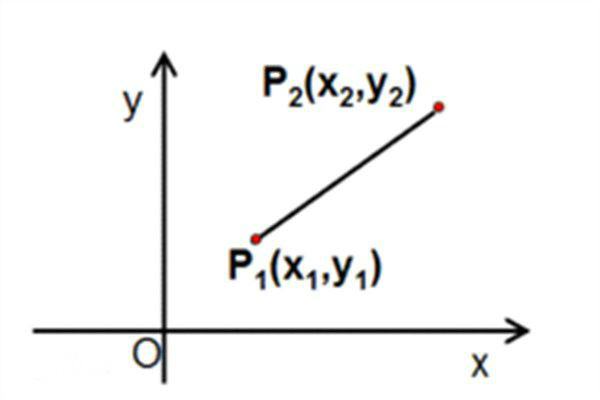
（2）当直线L的斜率存在时，点斜式y2—y1=k(X2—X1），

（3）当直线L在两坐标轴上存在非零截距时，有截距式X/a+y/b=1

（4）对于任意函数上任意一点，其斜率等于其切线与x轴正方向的夹角，即tanα

（5）斜率计算：ax+by+c=0中，k=-a/b.

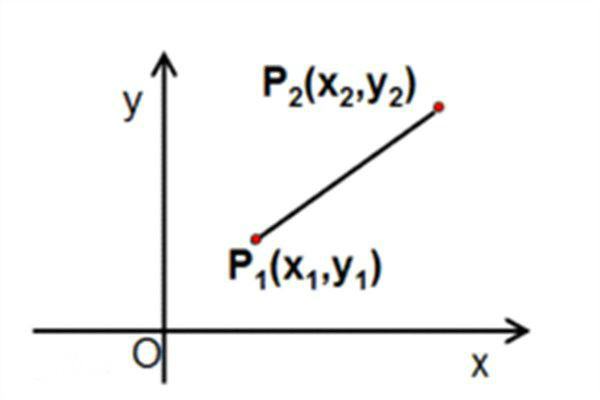
（6）直线斜率公式:k=(y2-y1)/(x2-x1)

（7）两条垂直相交直线的斜率相乘积为-1：k1*k2=-1

2、斜率的应用：

（1）求直线的倾斜角；

（2）证明三点共线；

（3）求参数的范围；

（4）求函数的值域(或最值)；

（5）证明不等式。

参考资料来源：百度百科 - 斜率

参考技术A

先求出曲线对应的函数的导函数，再把曲线上该点的横坐标代入导函数关系式，得到的函数值就是曲线上这一点的斜率。

过曲线上的某一点做一条切线，求切线的斜率，切线的斜率就是曲线在该点的斜率。

一条直线与某平面直角坐标系横坐标轴正半轴方向所成的角的正切值即该直线相对于该坐标系的斜率.如果直线与x轴互相垂直，直角的正切值无穷大，故此直线不存在斜率。当直线L的斜率存在时，对于一次函数y=kx+b，（斜截式）k即该函数图像的斜率。

扩展资料：

坐标平面内，每一条直线都有唯一的倾斜角，但不是每一条直线都有斜率，倾斜角是90°的直线（即x轴的垂线）没有斜率。

曲线的变化趋势仍可以用过曲线上一点的切线的斜率即导数来描述。导数的几何意义是该函数曲线在这一点上的切线斜率。

f'(x)>0时，函数在该区间内单调递增，曲线呈向上的趋势；f'(x)<0时，函数在该区间内单调减，曲线呈向下的趋势。

在（a，b）f''(x)<0时，函数在该区间内的图形是凸（从上向下看）的；f''(x)>0时，函数在该区间内的图形是凹的。

参考资料来源：百度百科--斜率

参考技术B 先求出曲线对应的函数的导函数，再把曲线上该点的横坐标代入导函数关系式，得到的函数值就是曲线上这一点的斜率。 参考技术C 如果你知道曲线的公式，计算该点的斜率就是斜率
如果不知道公式
取该曲线在这一点的切线斜率

也可以在该点附近走右取两点，求出斜率 参考技术D 对于任何一多项式f(x)=ax^n+bx^m+……
其斜率都等于anx^(n-1)+bmx^(m-1)+……

比方说抛物线f(x)=x^2，随便取一x值（就取x=2吧）
有f(2)=2^2=4
那么其在点（2，4）上的斜率等于1*2*(2^1)=4

晚来了3个月希望来的不算晚

如何在mathematica 5.0 中求曲线在某个区间的最大值和最小值和某点的斜率？

已经知道了曲线的形状，如何在mathematica 5 中求曲线在某个区间的最大值和最小值和某点的斜率？请高手帮忙了！

参考技术A 用FindMaximum和FindMinimum命令，然后结果中存在那个点的位置，你在用D[...]方法来把那个点导数求出来。这是连续函数的命令。

若是离散函数，你应该用Max,Min做，找那个点用Position命令，然后得出它点的位置，最后把那点用[[...]]给它挑出来，就是了，求导数用求差分的方法。

具体的你自己要把它编的很连贯，上下相接。 参考技术B 知道形状不行啊，要知道解析式
最大最小值是Maximum Minimum
斜率就是导数嘛，D[f[x],x0]，其中f[x]是曲线解析式，x0是要求斜率点的横坐标 参考技术C 对函数求导，然后把点代入。
D[f(x),x]/.x->3
Maximize
Minimize本回答被提问者采纳